« Previous « Start » Next »
5 Termination Test and Optimality
Internally in TOMLAB /KNITRO the problems solved by
Knitro
have the form
|
|
|
|
f(x) |
| subject to |
|
h(x) = 0 |
| |
|
g(x) ≤ 0. |
|
(3) |
The first-order conditions for identifying a locally optimal
solution
of the problem
3 are:
|
|
 x L x L |
(x,λ) =  f(x) + f(x) +
|
| |
| Σ |
i  E E |
|
λi hi(x) + hi(x) +
|
| |
| Σ |
i  I I |
|
λi gi(x) gi(x) |
|
= |
0 |
(4) |
| λi gi(x) |
= |
0, i  I I |
(5) |
| hi(x) |
= |
0, i  E E |
(6) |
| gi(x) |
≤ |
0, i  I I |
(7) |
| λi |
≥ |
0, i  I I |
(8) |
|
where
E and
I represent the sets of indices
corresponding to the equality constraints and inequality constraints
respectively, and λ
i is the Lagrange multiplier
corresponding to constraint
i. In TOMLAB /KNITRO we define the
feasibility error (
Feas err) at a point
xk to be the
maximum violation of the constraints
6,
7, i.e.,
| Feas err |
= |
| |
| max |
i  E E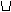 I I |
|
(0, |hi(xk)|, gi(xk)),
(9) |
while the optimality error (
Opt err) is defined as the
maximum violation of the first two conditions
4,
5,
|
Opt err |
= |
| |
| max |
i  I I |
|
(  x L(xk,λk) x L(xk,λk)  ∞, |λi gi(xk)|,
|λi|, |gi(xk)|).
(10) ∞, |λi gi(xk)|,
|λi|, |gi(xk)|).
(10) |
The last optimality condition
8 is enforced explicitly
throughout the optimization. In order to take into account problem
scaling in the termination test, the following scaling factors are
defined
|
|
| τ1 |
= |
max(1, |hi(x0)|, gi(x0)), |
(11) |
| τ2 |
= |
max(1,   f(xk) f(xk) ∞), ∞),
|
(12) |
|
where
x0 represents the initial point.
For unconstrained problems, the scaling
12 is not
effective since

 f
f(
xk)
 ∞
∞→ 0 as a
solution is approached.
Therefore, for unconstrained problems only, the following scaling is
used in the termination test
τ
2 = max(1, min(|
f(
xk)| ,

 f
f(
x0)
 ∞
∞)),
(13)
in place of
12.
TOMLAB /KNITRO stops and declares
LOCALLY OPTIMAL SOLUTION
FOUND if the following stopping conditions are satisfied:
|
|
| Feas err |
≤ |
max(τ1*FEASTOL, FEASTOLABS)
|
(14) |
| Opt err |
≤ |
max(τ2*OPTTOL,
OPTTOLABS)
|
(15) |
|
where
FEASTOL,
OPTTOL,
FEASTOLABS and
OPTTOLABS
are user-defined options (see Section
4.1).
This stopping test is designed to give the user much flexibility in
deciding when the solution returned by TOMLAB /KNITRO is accurate
enough. One can use a purely scaled stopping test (which is the
recommended default option) by setting
FEASTOLABS and
OPTTOLABS equal to
0.0e0. Likewise, an absolute
stopping test can be enforced by setting
FEASTOL and
OPTTOL equal to
0.0e0.
Unbounded problems
Since by default, TOMLAB /KNITRO uses a relative/scaled stopping
test it is possible for the optimality conditions to be satisfied
for an unbounded problem. For example, if τ
2 → ∞ while
the optimality error
10 stays bounded, condition
15 will eventually be satisfied for some
OPTTOL>0. If
you suspect that your problem may be unbounded, using an absolute
stopping test will allow TOMLAB /KNITRO to detect this.
« Previous « Start » Next »

 f(xk)
f(xk) ∞→ 0 as a
solution is approached.
Therefore, for unconstrained problems only, the following scaling is
used in the termination test
in place of 12.
∞→ 0 as a
solution is approached.
Therefore, for unconstrained problems only, the following scaling is
used in the termination test
in place of 12.