« Previous « Start » Next »
6 rbfSolve description
Following is a detailed description of the
rbfSolve
algorithm.
6.1 Summary
The manual considers global optimization of costly objective
functions, i.e. the problem of finding the global minimum when
there are several local minima and each function value takes
considerable CPU time to compute. Such problems often arise in
industrial and financial applications, where a function value could
be a result of a time-consuming computer simulation or optimization.
Derivatives are most often hard to obtain, and the algorithms
presented make no use of such information.
The emphasis is on a new method by Gutmann and Powell,
A radial
basis function method for global optimization. This method is a
response surface method, similar to the Efficient Global
Optimization (
EGO) method of Jones. The TOMLAB implementation of
the Radial Basis Function (
RBF) method is described in detail.
6.2 Introduction
The task of global optimization is to find the set of parameters
x
in the feasible region Ω ⊂
Rd for which the objective
function
f(
x) obtains its smallest value. In other words, a point
x* is a
global optimizer to
f(
x) on Ω, if
f(
x*) ≤
f(
x) for all
x 
Ω . On the other hand,
a point
x
is a
local optimizer to
f(
x), if
f(
x
) ≤
f(
x) for all
x in some neighborhood around
x.
Obviously, when the objective function has several local minima,
there could be solutions that are locally optimal but not globally
optimal and standard local optimization techniques are likely to get
stuck before the global minimum is reached. Therefore, some kind of
global search is needed to find the global minimum with some
reliability.
Previously a Matlab implementations of the
DIRECT [
3]
has been made, the new constrained
DIRECT [
12] and the
Efficient Global Optimization (
EGO) [
4] algorithms. The
implementations are part of the TOMLAB optimization environment. The
implementation of the
DIRECT algorithm is further discussed and
analyzed in Björkman, Holmstrom [
1]. Since the
objective functions in our applications often are expensive to
compute, we have to focus on very efficient methods. At the IFIP TC7
Conference on System Modelling and Optimization in Cambridge 1999,
Hans-Martin Gutmann presented his work on the
RBF algorithm
[
5]. The idea of the
RBF algorithm is to use radial
basis function interpolation to define a utility function (Powell
[
15]). The next point, where the original objective
function should be evaluated, is determined by optimizing on this
utility function. The combination of our need for efficient global
optimization software and the interesting ideas of Powell and
Gutmann led to the development of an improved
RBF algorithm
implemented in Matlab.
6.3 The RBF Algorithm
Our
RBF algorithm is based on the ideas presented by Gutmann
[
5, 8], with some extensions and further
development. The algorithm is implemented in the Matlab routine
rbfSolve.
The
RBF algorithm deals with problems of the form
where
f  R
R and
x,
xL,
xU  Rd
Rd. We assume that no
derivative information is available and that each function
evaluation is very expensive. For example, the function value could
be the result of a time-consuming experiment or computer simulation.
6.3.1 Description of the Algorithm
We now consider the question of choosing the next point
where the objective function should be evaluated. The idea of the
RBF algorithm is to use radial basis function interpolation and a
measure of `bumpiness' of a radial function, σ say. A target
value
fn* is chosen that is an estimate of the global minimum of
f. For each
y 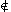
{
x1, … ,
xn} there exists a radial
basis function
sy that satisfies the interpolation conditions
|
|
| sy(xi) |
= |
f(xi), i=1, … ,n, |
| sy(y) |
= |
fn*. |
|
|
(2) |
The next point
xn+1 is calculated as the value of
y in the
feasible region that minimizes σ(
sy).
It turns out that the function
y 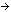
σ(
sy) is much
cheaper to compute than the original function.
Here, the radial basis function interpolant
sn has the form
|
sn(x) = |
|
λi  |

 |
½½ |
x−xi
|
½½ |
2 |

 |
+bTx + a,
(3) |
with λ
1,…,λ
n  R
R,
b  Rd
Rd,
a  R
R and

is either cubic with

(
r)=
r3 or the thin plate spline

(
r)=
r2 log
r. Gutmann considers other choices of

and
of the additional polynomial in [
6], but later in
[
7] concludes that the situation in the multiquadric and
Gaussian cases is disappointing.
The unknown parameters λ
i,
b and
a are obtained as the
solution of the system of linear equations
where Φ is the
n×
n matrix with
Φ
ij=

(
 xi
xi−
xj 2
2) and
|
P = |





 |
| x1T |
1 |
| x2T |
1 |
| . |
. |
| . |
. |
| xnT |
1 |
|
|





 |
, λ = |





 |
|
|





 |
, c = |







 |
|
|







 |
, F = |





 |
|
|





 |
.
(5) |
could be obtained accordingly, but there is no need to do that
as one is only interested in σ(
sy). In [
13] Powell
shows that if
the rank of
P is
d+1, then the matrix
is nonsingular and the linear system (
4) has a unique
solution.
Gutmann defines σ in [
8]. For
sn in
(
3) it is
Further, it is shown that σ(
sy) is
|
σ(sy) = σ(sn) + μn(y) |
[ |
sn(y)−fn* |
] |
2,
y 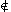 {x1, … ,xn}.
(8) {x1, … ,xn}.
(8) |
Thus minimizing σ(
sy) subject to constraints is equivalent
to minimizing
gn defined as
|
gn(y) = μn(y) |
[ |
sn(y)−fn* |
] |
2, y  Ω
\ Ω
\ |
{ |
x1, … ,xn |
} |
,
(9) |
where
μ
n(
y) is the coefficient corresponding to
y of the Lagrangian
function
L that satisfies
L(
xi)=0,
i=1, …,
n and
L(
y)=1. It can be computed as follows. Φ is extended to
where (
 y
y)
i=

(
 y
y−
xi 2
2),
i=1, … ,
n,
and
P is extended to
Then μ
n(
y) is the (
n+1)-th component of
v  Rn+d+2
Rn+d+2
that solves the system
We use the notation 0
n and 0
d+1 for column vectors with all
entries equal to zero and with dimension
n and (
d+1),
respectively.
The computation of μ
n(
y) is done for many different
y when
minimizing
gn(
y). This requires
O(
n3) operations if not
exploiting the structure of Φ
y and
Py. Hence it does not
make sense to solve the full system each time. A better alternative
is to factorize the interpolation matrix and update the
factorization for each
y. An algorithm that requires
O(
n2)
operations
is described in Section
6.3.3.
When there are large differences between function values, the
interpolant has a tendency to oscillate strongly. It might also
happen that min
sn(
y) is much lower than the best known function
value, which leads to a choice of
fn* that overemphasizes global
search. To handle these problems, large function values are in each
iteration replaced by the median of all computed function values.
Note that μ
n and
gn are not defined at
x1, … ,
xn
and
|
|
|
μn(y) = ∞, i=1, …, n.
(13) |
This will cause problems when μ
n is evaluated at a point close
to one of the known points. The function
hn(
x) defined by
|
hn(x) = |
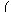

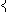

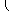 |
|
x 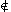 |
{ |
x1, … ,xn |
} |
|
| 0, |
x  |
{ |
x1, … ,xn |
} |
|
|
|
(14) |
is differentiable everywhere on Ω, and is thus a better
choice as objective function. Instead of minimizing
gn(
y) in
(
9) one may minimize −
hn(
y). In our implementation we
instead minimize −log(
hn(
y)).
By this we avoid a flat minimum and numerical trouble when
hn(
y)
is very small.
6.3.2 The Choice of fn*
For the value of
fn* it should hold that
fn*  |
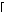
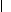
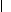
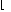 |
−∞, |
| |
| min |
y  Ω Ω |
|
sn(y) |
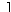
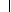
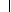
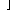 |
.
(15) |
The case
fn*=min
y  Ω sn
Ω sn(
y) is only
admissible if min
y  Ω sn
Ω sn(
y)<
sn(
xi),
i=1,
…,
n. There are two special cases for the choice of
fn*.
In the case when
fn*=min
y  Ω sn
Ω sn(
y), then
minimizing (
9) is equivalent to
|
|
| |
| min |
y  Ω Ω |
|
sn(y).
(16) |
In the case when
fn*=−∞, then minimizing (
9) is
equivalent to
|
|
| |
| min |
y  Ω \ Ω \ |
{ |
x1, … ,xn |
} |
|
|
μn(y).
(17) |
So how should
fn* be chosen? If
fn*=−∞, then the
algorithm will choose the new point in an unexplored region, which
is good from a global search point of view, but the objective
function will not be exploited at all. If
fn*=min
y  Ω sn
Ω sn(
y), the algorithm will show good local behaviour, but
the global minimum might be missed. Therefore, there is a need for a
mixture of values for
fn* close to and far away from
min
y  Ω sn
Ω sn(
y). Gutmann describes two different
strategies for the choice of
fn* in [
8].
The first strategy, denoted
idea 1, is to perform a cycle of
length
N+1 and choose
fn* as
|
fn* = |
| |
| min |
y  Ω Ω |
|
sn(y)−W
|



 |
|
f(xi)− |
| |
| min |
y  Ω Ω |
|
sn(y) |



 |
,
(18) |
with
where
ninit is the number of initial points. Here,
N=5 is
fixed and max
i f(
xi) is not taken over all points,
except for the first step of the cycle. In each of the subsequent
steps the
n−
nmax points with largest function value are removed
(not considered) when taking the maximum. Hence the quantity
max
i f(
xi) is decreasing until the cycle is over. Then
all points are considered again and the cycle starts from the
beginning. More formally, if (
n−
ninit)
mod(
N+1)=0,
nmax=
n, otherwise
|
nmax=max |
{ |
2,nmax−floor((n−ninit)/N)
|
} |
.
(20) |
The second strategy, denoted
idea 2, is to consider
fn* as
the optimal value of
|
|
| min |
f*(y) |
| s.t. |
| μn(y) |
[ |
sn(y)−f*(y) |
] |
2 ≤ αn2 |
|
| |
y  Ω, Ω, |
|
(21) |
and then perform a cycle of length
N+1 on the choice of
α
n. Here,
N=3 is fixed and
|
|
| αn |
= |
|



 |
|
f(xi)−
|
| |
| min |
y  Ω Ω |
|
sn(y) |



 |
, n=n0,n0+1 |
|
| αn0+2 |
= |
| min |
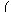
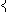
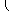 |
1, |
|



 |
|
f(xi)−
|
| |
| min |
y  Ω Ω |
|
sn(y) |



 |
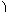
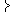
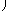 |
|
| αn0+3 |
= |
0, |
|
(22) |
where
n0 is set to
n at the beginning of each cycle. For this
strategy,
max
i f(
xi) is taken over all points in all parts of the
cycle.
Consider equation (
21).
Note that for a fixed
y the optimal
f*(
y) is the one for which
|
μn(y) |
[ |
sn(y)−f*(y) |
] |
2 = αn2.
(23) |
Substituting this equality constraint into the objective of
(
21) simplifies the problem to the minimization of
|
f*(y) = sn(y) − αn/√ |
|
.
(24) |
Denoting the minimizer of (
24) by
y*, and choosing
fn*=
f*(
y*), it is evident that
y* minimizes
μ
n(
y)[
sn(
y)−
fn*]
2 and hence
gn(
y) in
(
9).
For both strategies (
idea 1 and
idea 2), a check is
performed when (
n−
ninit)
mod(
N+1)=
N. This is the stage
when a purely local search is performed, so it is important to make
sure that the minimizer of
sn is not one of the interpolation
points or too close to one. The test used is
|
fmin− |
| |
| min |
y  Ω Ω |
|
sn(y) ≤ 10−4
max |
{ |
1,|fmin| |
} |
,
(25) |
where
fmin is the best function value found so far, i.e.
min
i f(
xi),
i=1, … ,
n. For the first strategy
(
idea 1), if (
25) is true, then
|
fn*= |
| |
| min |
y  Ω Ω |
|
sn(y)−10−2max |
{ |
1,|fmin| |
} |
,
(26) |
otherwise
fn* is set to 0. For the second strategy (
idea
2), if (
25) is true, then α
n (or more
correctly α
n0+3) is set to
|
αn0+3=min |
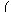
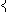
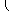 |
1, |
|



 |
|
f(xi)−
|
| |
| min |
y  Ω Ω |
|
sn(y) |



 |
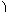
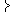
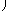 |
,
(27) |
otherwise α
n0+3 is set to 0.
6.3.3 Factorizations and Updates
In Powell [
14] a factorization algorithm is presented for
the solution of (
4). The
algorithm makes use of the conditional definiteness of Φ, i.e.
λ
T Φ λ > 0, λ ≠ 0 and
PT λ=0.
If
is the
QR decomposition of
P, then the columns of
Z span the
null space of
PT, and every λ with
PT λ=0 can be
expressed as λ=
Z z for some vector
z. Thus the conditional
positive definiteness implies that
zT ZT Φ
Z z > 0,
z  Rn−d−1
Rn−d−1 \ {0}.
(29)
This shows that
ZT Φ
Z is positive definite, and thus its
Cholesky factorization
exists. This property can be used to solve (
4) as
follows. Consider the interpolation condition Φ λ+
Pc=
F in
(
4). Multiply from left by
ZT and replace λ
by
Z z. Because
ZT P=0, the interpolation condition simplifies
to
Solving this system using the Cholesky factorization gives
z. Then
compute λ=
Z z and solve
for
c using the
QR decomposition of
P as
Rc = YT (F − Φ λ).
(33)
The same principle can be applied to solve (
12)
for a given
y to get μ
n(
y). In analogy to the discussion
above, if the extended matrices Φ
y and
Py in
(
10) and (
11), respectively, are given, and if
ZyT Py = 0
(34)
and
ZyT Φy Zy = Ly LyT
(35)
is the Cholesky factorization, then the vector
v = Zy z(y)
(36)
yields μ
n(
y) =
vn+1, where
z(
y) solves
The Cholesky factorization is the most expensive part of this
procedure. It requires
O(
n3) operations. As μ
n(
y) must be
computed for many different
y this is inacceptable. However, if
one knows the
QR factors of
P and the Cholesky factor of
ZT
Φ
Z, the
QR factorization of
Py and the new Cholesky factor
Ly can be computed in
O(
n2) operations.
The new Φ(
y) is
where (
 y
y)
i=

(
 y
y−
xi 2
2),
i=1, … ,
n.
The new
P(
y) is
Compute the
QR factorization of
Py, defined in
(
10). Given
P=
QR, the
QR factorization of
Py may
be written as
where
H is an orthogonal matrix obtained by
d+1 Givens rotations
and for
i=
d+2, …,
n the
i-th column of
H is the
i-th
unit vector. Denote
B=
QT Φ
Q. Using Φ
y as defined in
(
10) consider the expanded
B matrix
Multiplications from the right and left with
H affects only the
first (
d+1) rows and columns and the last row and the last columns
of the matrix in the middle. (Remember,
d is the dimension of the
problem). Hence
where * denotes entries not important for the moment.
From the form of
By it follows that
holds. The Cholesky factorization of
ZT Φ
Z is already known.
The new Cholesky
Ly factor is found by solving the lower
triangular system
L l =
v for
l, computing
β=√
γ−lTl, and setting
It is easily seen that
Ly LyT =
ZyT Φ
y Zy because
Note that in practice we do the following: First compute the
factorization of
P, i.e.
Py=
QyRy, using Givens rotations.
Then, since we are only interested in
v and γ in
(
42), it is not necessary to compute the matrix
By in
(
41). Setting
v to the last column in
Qy and
computing
v=Φ
yT v=Φ
y v (Φ
y is
symmetric), gives
v and γ by multiplying the last (
n−
d)
columns in
Qy by
v, i.e.
Using this algorithm,
v and γ are computed using ((
n+1) +
(
n−
d)) inner products instead of the two matrix multiplications in
(
41).
Note that the factorization algorithm is a normal `null-space'
method
for solving an optimization problem involving linear equality
constraints. The system of linear equations in (
4)
defines the necessary conditions for a stationary point to the
unconstrained quadratic programming (QP) problem
Viewing
c as Lagrange multipliers for the linear equalities in
(
4), (
47) is equivalent to the QP problem in
λ defined as
|
|
|
|
λ Φ λ − F
λ
subject to P λ = 0.
(48) |
The first condition in the conditional positive definiteness
definition is the same as saying that the reduced Hessian must be
positive definite at the solution of the QP problem if that solution
is to be unique.
The type of update procedure described above is suitable each time
an optimal point
y =
xn+1 is added. However, when evaluating
all candidates
y an even more efficient algorithm can be
formulated. What is needed is a black-box procedure to solve linear
systems with a general right-hand side:
ccΦPPT0
c λc =
c gr.
Using the
QR-factorization in (
28) the steps
| R v |
= |
r, |
| Z Φ Zw |
= |
Z (g − Φ Yv), |
| λ |
= |
Yv + Zw, |
| R c |
= |
Y(g − Φ λ) |
simplify when
r=0 as in (
4), but all steps are
useful for solving the extended system (
49); see next.
For each of many vectors
y, the extended system takes the form
cc|
cΦ
 P
P T
T0
pT
PTp0
c μ =
c 010,
(49)
where
p = (
yT 1 ). This permutes to
cc|
cΦ
P PT
PT0
p
 TpT
TpT0
c μ =
c 001,
(50)
which may be solved by block-LU factorization (also known as the
Schur-complement method). It helps that most of the right-hand side
is zero. The solution is given by the steps
| ccΦPPT0
c |
= |
c  p, p, |
| μ |
= |
−1 / ( + p ), + p ), |
| c |
= |
−μ c . |
Thus, each
y requires little more than solving for
(,) using the current factorizations (two operations
each with
Q,
R and
L). This is cheaper than updating the
factors for each
y, and should be reliable unless the matrix in
(
4) is nearly singular. The updating procedure is best
numerically, and it is still needed once when the final
y =
xn+1 is chosen.
6.3.4 A Compact Algorithm Description
Section
6.3.1-
6.3.3 described all the
elements of the
RBF algorithm as implemented in our Matlab
routine
rbfSolve, but our discussion has covered several
pages. We now summarize everything in a compact step-by-step
description. Steps 2, 6 and 7 are different in
idea 1 and
idea 2.
| |
idea 1 |
|
idea 2 |
| 1: |
Choose n initial points x1, … ,xn
(normally the 2d box corner points defined by the variable
bounds). Compute Fi=f(xi), i=1,2, … ,n
and set ninit=n. |
| 2: |
Start a cycle of length 6. |
|
Start a cycle of length 4. |
| 3: |
If the maximum number of function
evaluations reached, quit. |
| 4: |
Compute the radial basis function
interpolant sn by solving the system of linear
equations (4). |
| 5: |
Solve the minimization problem
miny  Ω sn(y). Ω sn(y). |
| 6: |
Compute fn* in (18) corresponding to the
current
position in the cycle. |
|
Compute αn in (22) corresponding to the current
position in the cycle. |
| 7: |
New point xn+1 is the value of y that minimizes
gn(y)
in (9). |
|
New point xn+1 is the value of y that minimizes f*(y)
in (24). |
| 8: |
Compute Fn+1=f(xn+1)
and set
n=n+1. |
| 9: |
If end of cycle, go to 2.
Otherwise go to 4. |
6.3.5 Some Implementation Details
The first question that arise is how to choose the points
x1,
… ,
xninit to include in the initial set. We only
consider box constrained problems, and choose the corners of the box
as initial points, i.e.
ninit=2
d. Starting with other points
is likely to lead to the corners during the iterations anyway. But
as Gutmann suggests, having a "good" point beforehand, one can
include it in the initial set.
The subproblem
|
|
| |
| min |
y  Ω Ω |
|
sn(y) |
|
,
(51) |
is itself a problem which could have more than one local minima. To
solve (
51) (at least approximately), we start from the
interpolation point with the least function value, i.e.
argmin f(
xi),
i=1, … ,
n, and perform a local
search. In many cases this leads to the minimum of
sn. Of course,
there is no guarantee that it does. We use analytical expressions
for the derivatives of
sn and perform the local optimization
using
ucSolve in TOMLAB [
9, 10] running the
inverse BFGS algorithm [
11].
To minimize
gn(
y) for the first strategy, or
f*(
y) for the
second strategy, we use our Matlab routine
glbSolve
implementing the
DIRECT algorithm (see the TOMLAB manual). We run
glbSolve for 500 function evaluations and choose
xn+1 as
the best point found by
glbSolve. When
(
n−
ninit)
mod(
N+1)=
N (when a purely local search is
performed) and the minimizer of
sn is not too close to any of the
interpolation points, i.e. (
25) is not true,
glbSolve is not used to minimize
gn(
y) or
f*(
y).
Instead, we choose the minimizer of (
51) as the new
point
xn+1.
The TOMLAB routine
AppRowQR is used to update the
QR
decomposition.
Our experience so far with the
RBF algorithm shows that for the
second strategy (
idea2), the minimum of (
24) is
very sensitive for the scaling of the box constraints. To overcome
this problem we transform the search space to the unit hypercube.
This algorithm improvement is necessary to avoid rank deficiency in
the interpolation matrix for the train design problem.
In our implementation it is possible to
restart the
optimization with the final status of all parameters from the
previous run.
« Previous « Start » Next »
 Ω . On the other hand,
a point x
is a local optimizer to f(x), if f( x
) ≤ f(x) for all x in some neighborhood around x.
Obviously, when the objective function has several local minima,
there could be solutions that are locally optimal but not globally
optimal and standard local optimization techniques are likely to get
stuck before the global minimum is reached. Therefore, some kind of
global search is needed to find the global minimum with some
reliability.
Ω . On the other hand,
a point x
is a local optimizer to f(x), if f( x
) ≤ f(x) for all x in some neighborhood around x.
Obviously, when the objective function has several local minima,
there could be solutions that are locally optimal but not globally
optimal and standard local optimization techniques are likely to get
stuck before the global minimum is reached. Therefore, some kind of
global search is needed to find the global minimum with some
reliability. R and x, xL, xU
R and x, xL, xU  Rd. We assume that no
derivative information is available and that each function
evaluation is very expensive. For example, the function value could
be the result of a time-consuming experiment or computer simulation.
Rd. We assume that no
derivative information is available and that each function
evaluation is very expensive. For example, the function value could
be the result of a time-consuming experiment or computer simulation.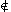 {x1, … ,xn} there exists a radial
basis function sy that satisfies the interpolation conditions
The next point xn+1 is calculated as the value of y in the
feasible region that minimizes σ(sy).
It turns out that the function y
{x1, … ,xn} there exists a radial
basis function sy that satisfies the interpolation conditions
The next point xn+1 is calculated as the value of y in the
feasible region that minimizes σ(sy).
It turns out that the function y 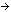 σ(sy) is much
cheaper to compute than the original function.
σ(sy) is much
cheaper to compute than the original function. R, b
R, b  Rd, a
Rd, a  R and
R and
 is either cubic with
is either cubic with  (r)=r3 or the thin plate spline
(r)=r3 or the thin plate spline
 (r)=r2 logr. Gutmann considers other choices of
(r)=r2 logr. Gutmann considers other choices of  and
of the additional polynomial in [6], but later in
[7] concludes that the situation in the multiquadric and
Gaussian cases is disappointing.
and
of the additional polynomial in [6], but later in
[7] concludes that the situation in the multiquadric and
Gaussian cases is disappointing. (
( xi−xj
xi−xj 2) and
2) and




















































 y)i=
y)i= (
( y−xi
y−xi 2), i=1, … ,n,
and P is extended to
Then μn(y) is the (n+1)-th component of v
2), i=1, … ,n,
and P is extended to
Then μn(y) is the (n+1)-th component of v  Rn+d+2
that solves the system
We use the notation 0n and 0d+1 for column vectors with all
entries equal to zero and with dimension n and (d+1),
respectively.
The computation of μn(y) is done for many different y when
minimizing gn(y). This requires O(n3) operations if not
exploiting the structure of Φy and Py. Hence it does not
make sense to solve the full system each time. A better alternative
is to factorize the interpolation matrix and update the
factorization for each y. An algorithm that requires O(n2)
operations
is described in Section 6.3.3.
Rn+d+2
that solves the system
We use the notation 0n and 0d+1 for column vectors with all
entries equal to zero and with dimension n and (d+1),
respectively.
The computation of μn(y) is done for many different y when
minimizing gn(y). This requires O(n3) operations if not
exploiting the structure of Φy and Py. Hence it does not
make sense to solve the full system each time. A better alternative
is to factorize the interpolation matrix and update the
factorization for each y. An algorithm that requires O(n2)
operations
is described in Section 6.3.3. Ω sn(y) is only
admissible if miny
Ω sn(y) is only
admissible if miny  Ω sn(y)<sn(xi), i=1,
…, n. There are two special cases for the choice of fn*.
In the case when fn*=miny
Ω sn(y)<sn(xi), i=1,
…, n. There are two special cases for the choice of fn*.
In the case when fn*=miny  Ω sn(y), then
minimizing (9) is equivalent to
In the case when fn*=−∞, then minimizing (9) is
equivalent to
So how should fn* be chosen? If fn*=−∞, then the
algorithm will choose the new point in an unexplored region, which
is good from a global search point of view, but the objective
function will not be exploited at all. If fn*=miny
Ω sn(y), then
minimizing (9) is equivalent to
In the case when fn*=−∞, then minimizing (9) is
equivalent to
So how should fn* be chosen? If fn*=−∞, then the
algorithm will choose the new point in an unexplored region, which
is good from a global search point of view, but the objective
function will not be exploited at all. If fn*=miny  Ω sn(y), the algorithm will show good local behaviour, but
the global minimum might be missed. Therefore, there is a need for a
mixture of values for fn* close to and far away from
miny
Ω sn(y), the algorithm will show good local behaviour, but
the global minimum might be missed. Therefore, there is a need for a
mixture of values for fn* close to and far away from
miny  Ω sn(y). Gutmann describes two different
strategies for the choice of fn* in [8].
Ω sn(y). Gutmann describes two different
strategies for the choice of fn* in [8]. y)i=
y)i= (
( y−xi
y−xi 2), i=1, … ,n.
The new P(y) is
Compute the QR factorization of Py, defined in
(10). Given P=QR, the QR factorization of Py may
be written as
where H is an orthogonal matrix obtained by d+1 Givens rotations
and for i=d+2, …, n the i-th column of H is the i-th
unit vector. Denote B=QT Φ Q. Using Φy as defined in
(10) consider the expanded B matrix
Multiplications from the right and left with H affects only the
first (d+1) rows and columns and the last row and the last columns
of the matrix in the middle. (Remember, d is the dimension of the
problem). Hence
where * denotes entries not important for the moment.
From the form of By it follows that
holds. The Cholesky factorization of ZT Φ Z is already known.
The new Cholesky Ly factor is found by solving the lower
triangular system L l = v for l, computing
β=√γ−lTl, and setting
It is easily seen that Ly LyT = ZyT Φy Zy because
2), i=1, … ,n.
The new P(y) is
Compute the QR factorization of Py, defined in
(10). Given P=QR, the QR factorization of Py may
be written as
where H is an orthogonal matrix obtained by d+1 Givens rotations
and for i=d+2, …, n the i-th column of H is the i-th
unit vector. Denote B=QT Φ Q. Using Φy as defined in
(10) consider the expanded B matrix
Multiplications from the right and left with H affects only the
first (d+1) rows and columns and the last row and the last columns
of the matrix in the middle. (Remember, d is the dimension of the
problem). Hence
where * denotes entries not important for the moment.
From the form of By it follows that
holds. The Cholesky factorization of ZT Φ Z is already known.
The new Cholesky Ly factor is found by solving the lower
triangular system L l = v for l, computing
β=√γ−lTl, and setting
It is easily seen that Ly LyT = ZyT Φy Zy because
 p,
p, + p ),
+ p ), Ω sn(y).
Ω sn(y).