« Previous « Start
3 TOMLAB /PENOPT Solver Reference
The PENOPT solvers are a set of solvers that were developed by the
PENOPT GbR. Table
1 lists the solvers included in
TOMLAB /PENOPT. The solvers are called using a set of MEX-file
interfaces developed as part of TOMLAB . All functionality of the
PENOPT solvers are available and changeable in the TOMLAB framework
in Matlab .
Detailed descriptions of the TOMLAB /PENOPT solvers are given in
the following sections. Also see the M-file help for each solver.
Additional solvers reference guides for the TOMLAB /PENOPT solvers
are available for download from the TOMLAB home page
http://tomopt.com. Extensive TOMLAB m-file help is also
available, for example
help penbmiTL in Matlab will display
the features of the PENBMI solver using the TOMLAB format.
TOMLAB /PENOPT solves
The
linear semi-definite programming problem with linear
matrix inequalities (
sdp) is defined as
|
|
|
f(x) = cTx |
| |
|
| s/t |
xL |
≤ |
x |
≤ |
xU |
| |
bL |
≤ |
Ax |
≤ |
bU |
| |
| Q0i + |
|
n Qkixk 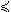 0, i=1,…,m. 0, i=1,…,m. |
|
|
(1) |
where
c,
x,
xL,
xU  Rn
Rn,
A  Rml
× n
Rml
× n,
bL,
bU  Rml
Rml and
Qki are
symmetric matrices of similar dimensions in each constraint
i.
If there are several LMI constraints, each may have it's own
dimension.
The
linear semi-definite programming problem with bilinear
matrix inequalities (
bmi) is defined similarly to
(
1) but with the matrix following inequality
constraints
|
|
Q0i + |
|
n Qkixk + |
|
n |
|
n xkxlKkli 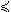 0 (2) 0 (2) |
The MEX solvers
pensdp and
penbmi treat
sdp and
bmi problems, respectively. These are available in the
TOMLAB /PENSDP and TOMLAB /PENBMI toolboxes.
The MEX-file solver
pensdp available in the TOMLAB /PENSDP toolbox
implements a penalty method aimed at large-scale dense and sparse
sdp problems. The interface to the solver allows for data
input in the sparse SDPA input format as well as a TOMLAB specific
format corresponding to (
1).
The MEX-file solver
penbmi available in the TOMLAB /PENBMI toolbox
is similar to
pensdp , with added support for the bilinear
matrix inequalities (
2).
The add-on toolbox TOMLAB /PENOPT solves linear semi-definite
programming problems with linear and bilinear matrix inequalities.
The solvers are listed in Table
1. They are written
in a combination of Matlab and C code.
Table 1: Solvers in TOMLAB /PENOPT.
|
| Function |
Description |
Reference |
|
| penbmi |
Sparse and dense linear semi-definite programming using a penalty algorithm.
|
|
| penfeas_sdp |
Feasibility check of systems of
linear matrix inequalities, using pensdp .
|
|
|
|
| pensdp |
Sparse and dense linear semi-definite programming using a penalty algorithm.
|
|
| penfeas_sdp |
Feasibility check of systems of
linear matrix inequalities, using pensdp .
|
|
|
3.1 PENBMI
TOMLAB /PENBMI was developed in co-operation with PENOPT GbR. The
following pages describe the solvers and the feasibility checks.
3.1.1 penfeas_bmi
Purpose
penfeas_bmi checks the feasibility of a system of
bilinear matrix inequalities (BMI):
|
Ai0 +
|
|
n Ak(i) xk +
|
|
n |
|
n xk xl Kkl(i)
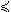 0, k=1,2,…,m 0, k=1,2,…,m
|
with symmetric matrices
Aki,
Kkli  Rdl × dl
Rdl × dl,
k,
l=1,…,
n,
i=1,…,
m
and
x  Rn
Rn.
Calling Syntax
[
ifeas,
feas,
xfeas ] = penfeas_bmi(p, x_0, options)
Description of Inputs
p PENBMI format structure, e.g. from
sdpa2pen .
x_0 Inital guess of the feasible point. Default = 0.
options Optional 3 × 1 vector.
May be omitted, in which case the defaults below are used.
| options(1) |
Output level of PENBMI solver. Default = 0. |
| options(2) |
Upper bound on  x x ∞. Default = 1000. ∞. Default = 1000. |
| |
If <0, no box bounds are applied. |
| options(3) |
Weighting parameter in the objective function. Default 10−4. |
Description of Outputs
ifeas Feasibility of the system:
| 0 |
System is strictly feasible |
| 1 |
System is feasible but not necessarily strictly feasible |
| -1 |
System is probably infeasible |
feas Value of the minimized maximal eigenvalue of BMI.
xfeas Feasible point
Algorithm
The feasibility of the system of BMI's is checked by solving the
following
bmi problem:
|
|
| |
| min |
x Rn,λ Rn,λ R R |
|
f(x,λ) = λ + w  x x 22 22 |
| s.t. |
− xbound |
≤ |
x |
≤ |
xbound |
| |
| A0i + |
|
n Aki xk
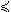 λ In × n, λ In × n, |
|
i=1,…,m |
|
where
xbound is taken from input argument
options(2) ,
or ∞ if
options(2) <0.
When λ < 0, the system is strictly feasible;
when λ=0, the system is feasible but has no interior point.
When λ>0 for any
xbound, the system may be infeasible.
As the semidefinite problem solved is nonconvex and
penbmiQ
is a local method, it cannot be guaranteed that the solution
λ is a global minimum. Consequently, the (local) optimum
λ
loc found by
penbmiQ may be a positive number
(indicating infeasibility), although the system is feasible (i.e.,
the global optimum λ
glob<0). In such a case, the user may
try various initial points
x_0, and also different weighting
parameter
w (
option(3) ).
In practice, the conditions on feasibility are as follows:
λ < −10
−6 means strict feasibility,
|λ|<10
−6 means feasibility (not strict) and
λ > 10
−6 indicates infeasibility.
The user can decide by the actual value of the output parameter
feas
(including the optimal λ).
For the case when the BMI system is unbounded, we have to add
artificial bounds on
x, otherwise PENBMI might diverge. Of course,
it may happen that the feasible point lies outside these bounds. In
this case
penfeas_bmi claims infeasibility, although the system
is actually feasible. When in doubts, the user may try to gradually
increase
xbound (parameter
options(2) ).
On the other hand, for very ill-conditioned and unbounded systems, the
default bound 1000 may be too large and PENBMI may not converge. In
this case, the user is advised either to increase the weighting
parameter
w (to 0.01 and bigger) or to decrease the bound
(parameter
options(2) ) to a smaller number (100–1).
M-files Used
pen.m
MEX-files Used
penbmiQ
See Also
penfeas_sdp.m
Purpose
Solve (linear) semi-definite programming problems.
penbmiTL solves problems of the form
|
|
|
f(x) = cT x |
|
| |
| s/t |
xL |
≤ |
x |
≤ |
xU |
|
| |
bL |
≤ |
Ax |
≤ |
bU |
|
| |
|
|
|
Qi(0) +
|
|
n Qk(i) xk +
|
|
n |
|
n xk xl Kkl(i)
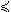 0, k=1,2,…,m 0, k=1,2,…,m
|
|
|
|
(3) |
where
x,
xL,
xU  Rn
Rn,
A  Rml × n
Rml × n,
bL,
bU
 Rml
Rml and
Qk(i) are sparse or dense symmetric
matrices. The matrix sizes may vary between different matrix
inequalities but must be the same in each particular constraint.
Calling Syntax
Result = tomRun('penbmi',Prob,...)
Description of Inputs
| Prob |
Problem description structure. The following fields are used: |
| |
| |
QP.c |
Vector with coefficients for linear objective function. |
| |
| |
A |
Linear constraints matrix. |
| |
b_L |
Lower bound for linear constraints. |
| |
b_U |
Upper bound for linear constraints. |
| |
| |
x_L |
Lower bound on variables. |
| |
x_U |
Upper bound on variables. |
| |
| |
x_0 |
Starting point. |
| |
| |
PENOPT |
Structure with special fields for SDP parameters. Fields used are: |
| |
| |
LMI |
Structure array with matrices for the
linear terms of the matrix inequalities.
See Examples in § 3.2.2
for a discussion of how to set this correctly. |
| |
| |
ioptions |
8× 1 vector with options,
defaults in (). Any element set to a value less than zero will
be replaced by a default value, in some cases fetched from standard Tomlab parameters. |
| |
| |
ioptions(1) |
0/1: use default/user defined values for options. |
| |
ioptions(2) |
Maximum number of iterations for overall algorithm (50). If not given, Prob.optParam.MaxIter is used. |
| |
ioptions(3) |
Maximum number of iterations in unconstrained optimization (100). If not given, Prob.optParam.MinorIter is used. |
| |
ioptions(4) |
Output level: 0/(1)/2/3 = silent / summary / brief / full. |
| |
ioptions(5) |
(0)/1: Check density of Hessian / Assume dense. |
| |
ioptions(6) |
(0)/1: (Do not) use linesearch in unconstrained minimization. |
| |
ioptions(7) |
(0)/1: (Do not) write solution vector to output file. |
| |
ioptions(8) |
(0)/1: (Do not) write computed multipliers to output file. |
| |
| |
foptions |
1 × 7 vector with options, defaults in (). |
| |
| |
foptions(1) |
Scaling factor linear constraints; must be positive. (1.0). |
| |
foptions(2) |
Restriction for multiplier update; linear constraints (0.7). |
| |
foptions(3) |
Restriction for multiplier update; matrix constraints (0.1). |
| |
foptions(4) |
Stopping criterium for overall algorithm (10−7). Tomlab equivalent: Prob.optParam.eps_f . |
| |
foptions(5) |
Lower bound for the penalty parameters (10−6). |
| |
foptions(6) |
Lower bound for the multipliers (10−14). |
| |
foptions(7) |
Stopping criterium for unconstrained minimization (10−2). |
| |
Description of Outputs
| Result |
Structure
with result from optimization.
The following fields are changed: |
| |
| |
x_k |
Optimal point. |
| |
f_k |
Function value at optimum. |
| |
g_k |
Gradient value at optimum, c. |
| |
v_k |
Lagrange multipliers. |
| |
| |
x_0 |
Starting point. |
| |
f_0 |
Function value at start. |
| |
| |
xState |
State of each variable, described in the TOMLAB User's Guide. |
| |
| |
Iter |
Number of iterations. |
| |
ExitFlag |
0: OK. |
| |
|
1: Maximal number of iterations reached. |
| |
|
2: Unbounded feasible region. |
| |
|
3: Rank problems. Can not find any solution point. |
| |
|
4: Illegal x_0 . |
| |
|
5: No feasible point x_0 found. |
| |
| |
Inform |
If ExitFlag > 0, Inform=ExitFlag. |
| |
QP.B |
Optimal active set. See input variable QP.B . |
| |
| |
Solver |
Solver used. |
| |
SolverAlgorithm |
Solver algorithm used. |
| |
FuncEv |
Number of function evaluations. Equal to Iter . |
| |
ConstrEv |
Number of constraint evaluations. Equal to Iter . |
| |
Prob |
Problem structure used. |
| |
Description
pensdp implements a penalty algorithm based on the PBM method
of Ben-Tal and Zibulevsky. It is possible to give input data in three different formats:
-
Standard sparse SPDA format
- PENSDP Structural format
- Tomlab Quick format
In all three cases, problem setup is done via
sdpAssign .
See Also
sdpAssign.m ,
sdpa2pen.m ,
sdpDemo.m ,
tomlab/docs/penbmi.pdf
Warnings
Currently
penbmi does not work well solving problems of
sdp type.
Examples
Setting the LMI constraints is best described by an example. Assume 3
variables
x=(
x1,
x2,
x3) and 2 linear matrix inequalities of sizes
3× 3 and 2× 2 respectively, here given on block-diagonal
form:
The
LMI structure could then be initialized with the following commands:
% Constraint 1
>> LMI(1,1).Q0 = [];
>> LMI(1,1).Q = [2 -1 0 ; ...
0 2 0 ; ...
0 0 2];
>> LMI(1,2).Q = [];
>> LMI(1,3).Q = [2 0 -1 ; ...
0 2 0 ; ...
0 0 2];
% Constraint 2, diagonal matrices only
>> LMI(2,1).Q0 = diag( [0, 1] );
>> LMI(2,1).Q = diag( [1,-1] );
>> LMI(2,2).Q = diag( [3,-3] );
>> LMI(2,3).Q = [ ];
% Use LMI in call to sdpAssign:
>> Prob=sdpAssign(c,LMI,...)
% ... or set directly into Prob.PENSDP.LMI field:
>> Prob.PENSDP.LMI = LMI;
Some points of interest:
-
The LMI structure must be of correct size. This is
important if a LMI constraint has zero matrices for the highest
numbered variables. If the above example had zero coefficient
matrices for x3, the user would have to set LMI(1,3).Q =
[] explicitly, so that the LMI structure array is really 2
× 3. (LMI(2,3).Q would automatically become empty in
this case, unless set otherwise by the user).
- MATLAB sparse format is allowed and encouraged.
- Only the upper triangular part of each matrix is used
(symmetry is assumed).
Input in Sparse SDPA Format is handled by the conversion routine
sdpa2pen . For example, the problem defined in
tomlab/examples/arch0.dat-s can be solved using the following
statements:
>> p = sdpa2pen('arch0.dat-s')
p =
vars: 174
fobj: [1x174 double]
constr: 174
ci: [1x174 double]
bi_dim: [1x174 double]
bi_idx: [1x174 double]
bi_val: [1x174 double]
mconstr: 1
ai_dim: 175
ai_row: [1x2874 double]
ai_col: [1x2874 double]
ai_val: [1x2874 double]
msizes: 161
ai_idx: [175x1 double]
ai_nzs: [175x1 double]
x0: [1x174 double]
ioptions: 0
foptions: []
>> Prob = sdpAssign(p); % Can call sdpAssign with only 'p' structure
>> Result = tomRun('pensdp',Prob); % Call tomRun to solve problem
3.2 PENSDP
TOMLAB /PENSDP was developed in co-operation with PENOPT GbR. The
following pages describe the solvers and the feasibility checks.
3.2.1 penfeas_sdp
Purpose
penfeas_sdp checks the feasibility of a system of
linear matrix inequalities (LMI):
|
A0i + |
|
n Aki xk 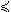 0, i=1,…,m 0, i=1,…,m
|
with symmetric matrices
Aki  Rdl × dl
Rdl × dl,
k=1,…,
n,
i=1,…,
m
and
x  Rn
Rn.
Calling Syntax
[
ifeas,
feas,
xfeas] = penfeas_sdp(p, options )
Description of Inputs
p PENSDP format structure, e.g. from
sdpa2pen .
options Optional 2 × 1 vector.
May be omitted, in which case the defaults below are used.
| options(1) |
Output level of PENSDP solver. Default = 0. |
| options(2) |
Upper bound on  x x ∞. Default = 1000. ∞. Default = 1000. |
| |
If <0, no box bounds are applied. |
Description of Outputs
ifeas Feasibility of the system:
| 0 |
System is strictly feasible |
| 1 |
System is feasible but not necessarily strictly feasible |
| -1 |
System is probably infeasible |
feas Value of the minimized maximal eigenvalue of LMI.
xfeas Feasible point
Algorithm
The feasibility of the system of LMI's is checked by solving the
following
sdp problem:
|
|
| |
| min |
x Rn,λ Rn,λ R R |
|
f(x,λ) = λ |
| s.t. |
− xbound |
≤ |
x |
≤ |
xbound |
| |
| A0i + |
|
n Aki xk
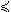 λ In × n, λ In × n, |
|
i=1,…,m |
|
where
xbound is taken from input argument
options(2) ,
or ∞ if
options(2) <0.
When λ < 0, the system is strictly feasible;
when λ=0, the system is feasible but has no interior point.
When λ>0 for any
xbound, the system is infeasible.
In practice, the conditions on feasibility are as follows:
λ < −10
−6 means strict feasibility,
|λ|<10
−6 means feasibility (not strict) and
λ > 10
−6 indicates infeasibility.
The user can decide by the actual value of the output parameter
feas
(including the optimal λ).
For the case when the LMI system is unbounded, we have to add
artificial bounds on
x, otherwise PENSDP might diverge. Of course,
it may happen that the feasible point lies outside these bounds. In
this case
penfeas_sdp claims infeasibility, although the system
is actually feasible. When in doubts, the user may try to gradually
increase
xbound (parameter
options(2) ). On the other
hand, for very ill-conditioned and unbounded systems, the default
bound 1000 may be too large and PENSDP may not converge. In this case,
the user is advised to decrease parameter
options(2) to a
smaller number (100–1).
M-files Used
pen.m
MEX-files Used
pensdp
See Also
penfeas_bmi.m
Purpose
Solve (linear) semi-definite programming problems.
pensdpTL solves problems of the form
|
|
|
f(x) = cT x |
|
| |
| s/t |
xL |
≤ |
x |
≤ |
xU |
|
| |
bL |
≤ |
Ax |
≤ |
bU |
|
| |
| |
|
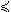 |
0, |
k=1,2,…,mLMI |
|
(4) |
where
x,
xL,
xU  Rn
Rn,
A  Rml × n
Rml × n,
bL,
bU
 Rml
Rml and
Qk(i) are sparse or dense symmetric matrices.
The matrix sizes may vary between different linear matrix inequalities
(
LMI) but must be the same in each particular constraint.
Calling Syntax
Result = tomRun('pensdp',Prob,...)
Description of Inputs
| Prob |
Problem description structure. The following fields are used: |
| |
| |
QP.c |
Vector with coefficients for linear objective function. |
| |
| |
A |
Linear constraints matrix. |
| |
b_L |
Lower bound for linear constraints. |
| |
b_U |
Upper bound for linear constraints. |
| |
| |
x_L |
Lower bound on variables. |
| |
x_U |
Upper bound on variables. |
| |
| |
x_0 |
Starting point. |
| |
| |
PriLevOpt |
Print level in pensdpTL and MEX interface. The print level in the solver is controlled by PENOPT.ioptions(4) . |
| |
PENOPT |
Structure with special fields for SDP parameters. Fields used are: |
| |
| |
LMI |
Structure array with matrices for the
linear matrix inequalities.
See Examples in § 3.2.2
for a discussion of how to set this correctly. |
| |
| |
ioptions |
8× 1 vector with options, defaults in (). Any element set to a value less than zero will
be replaced by a default value, in some cases fetched from standard Tomlab parameters. |
| |
| |
ioptions(1) |
0/1: use default/user defined values for options. |
| |
ioptions(2) |
Maximum number of iterations for overall algorithm (50). If not given, Prob.optParam.MaxIter is used. |
| |
ioptions(3) |
Maximum number of iterations in unconstrained optimization (100). If not given, Prob.optParam.MinorIter is used. |
| |
ioptions(4) |
Output level: 0/(1)/2/3 = silent/summary/brief/full. Tomlab parameter: Prob.PriLevOpt . |
| |
ioptions(5) |
(0)/1: Check density of Hessian / Assume dense. |
| |
ioptions(6) |
(0)/1: (Do not) use linesearch in unconstrained minimization. |
| |
ioptions(7) |
(0)/1: (Do not) write solution vector to output file. |
| |
ioptions(8) |
(0)/1: (Do not) write computed multipliers to output file. |
| |
| |
foptions |
7 × 1 vector with optimization parameters, defaults in (): |
| |
foptions(1) |
Scaling factor linear constraints; must be positive. (1.0). |
| |
foptions(2) |
Restriction for multiplier update; linear constraints (0.7). |
| |
foptions(3) |
Restriction for multiplier update; matrix constraints (0.1). |
| |
foptions(4) |
Stopping criterium for overall algorithm (10−7). Tomlab equivalent: Prob.optParam.eps_f . |
| |
foptions(5) |
Lower bound for the penalty parameters (10−6). |
| |
foptions(6) |
Lower bound for the multipliers (10−14). |
| |
foptions(7) |
Stopping criterium for unconstrained minimization (10−2). |
| |
Description of Outputs
| Result |
Structure
with result from optimization.
The following fields are changed: |
| |
| |
x_k |
Optimal point. |
| |
f_k |
Function value at optimum. |
| |
g_k |
Gradient value at optimum, c. |
| |
v_k |
Lagrange multipliers. |
| |
| |
x_0 |
Starting point. |
| |
f_0 |
Function value at start. |
| |
| |
xState |
State of each variable, described in the TOMLAB User's Guide. |
| |
| |
Iter |
Number of iterations. |
| |
ExitFlag |
0: OK. |
| |
|
1: Maximal number of iterations reached. |
| |
|
2: Unbounded feasible region. |
| |
|
3: Rank problems. Can not find any solution point. |
| |
|
4: Illegal x_0 . |
| |
|
5: No feasible point x_0 found. |
| |
| |
Inform |
If ExitFlag > 0, Inform=ExitFlag. |
| |
QP.B |
Optimal active set. See input variable QP.B . |
| |
| |
Solver |
Solver used. |
| |
SolverAlgorithm |
Solver algorithm used. |
| |
FuncEv |
Number of function evaluations. Equal to Iter . |
| |
ConstrEv |
Number of constraint evaluations. Equal to Iter . |
| |
Prob |
Problem structure used. |
| |
Description
pensdp implements a penalty algorithm based on the PBM method
of Ben-Tal and Zibulevsky. It is possible to give input data in three different formats:
-
Standard sparse SPDA format
- PENSDP Structural format
- Tomlab Quick format
In all three cases, problem setup is done via
sdpAssign .
See Also
sdpAssign.m ,
sdpa2pen.m ,
sdpDemo.m ,
tomlab/docs/pensdp.pdf,
penfeas_sdp.m
Examples
Setting the LMI constraints is best described by an example. Assume 3
variables
x=(
x1,
x2,
x3) and 2 linear matrix inequalities of sizes
3× 3 and 2× 2 respectively, here given on block-diagonal
form:
The
LMI structure should then be initialized with the following commands:
% Constraint 1
>> LMI(1,1).Q0 = [ ];
>> LMI(1,1).Q = [2 -1 0 ; ...
0 2 0 ; ...
0 0 2 ];
>> LMI(1,2).Q = [ ];
>> LMI(1,3).Q = [ 2 0 -1 ; ...
0 2 0 ; ...
0 0 2 ];
% Constraint 2, diagonal matrices only
>> LMI(2,1).Q0 = diag( [0, 1] );
>> LMI(2,1).Q = diag( [1,-1] );
>> LMI(2,2).Q = diag( [3,-3] );
>> LMI(2,3).Q = [ ];
% Use LMI in call to sdpAssign:
>> Prob=sdpAssign(c,LMI,...)
Some points of interest:
-
The LMI structure must be of correct size. This is
important if a LMI constraint has zero matrices for the highest
numbered variables. If the above example had zero coefficient
matrices for x3, the user would have to set LMI(1,3).Q =
[] explicitly, so that the LMI structure array is really 2
× 3. (LMI(2,3).Q would automatically become empty in
this case, unless set otherwise by the user).
- MATLAB sparse format is allowed and encouraged.
- Only the upper triangular part of each matrix is used
(symmetry is assumed).
Input in Sparse SDPA Format is handled by the conversion routine
sdpa2pen . For example, the problem defined in
tomlab/examples/arch0.dat-s can be solved using the following
statements:
>> p = sdpa2pen('arch0.dat-s')
p =
vars: 174
fobj: [1x174 double]
constr: 174
ci: [1x174 double]
bi_dim: [1x174 double]
bi_idx: [1x174 double]
bi_val: [1x174 double]
mconstr: 1
ai_dim: 175
ai_row: [1x2874 double]
ai_col: [1x2874 double]
ai_val: [1x2874 double]
msizes: 161
ai_idx: [175x1 double]
ai_nzs: [175x1 double]
x0: [1x174 double]
ioptions: 0
foptions: []
>> Prob=sdpAssign(p); % Can call sdpAssign with only 'p' structure
>> Result=tomRun('pensdp',Prob); % Call tomRun to solve problem
« Previous « Start
 Rn, A
Rn, A  Rml
× n, bL,bU
Rml
× n, bL,bU  Rml and Qki are
symmetric matrices of similar dimensions in each constraint i.
If there are several LMI constraints, each may have it's own
dimension.
Rml and Qki are
symmetric matrices of similar dimensions in each constraint i.
If there are several LMI constraints, each may have it's own
dimension.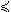 0, k=1,2,…,m
0, k=1,2,…,m
 Rdl × dl, k,l=1,…,n, i=1,…,m
and
x
Rdl × dl, k,l=1,…,n, i=1,…,m
and
x  Rn.
Rn. x
x ∞. Default = 1000.
∞. Default = 1000. Rn, A
Rn, A  Rml × n, bL,bU
Rml × n, bL,bU
 Rml and Qk(i) are sparse or dense symmetric
matrices. The matrix sizes may vary between different matrix
inequalities but must be the same in each particular constraint.
Rml and Qk(i) are sparse or dense symmetric
matrices. The matrix sizes may vary between different matrix
inequalities but must be the same in each particular constraint.















































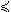 0
0
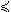 0, i=1,…,m
0, i=1,…,m
 Rdl × dl, k=1,…,n, i=1,…,m
and
x
Rdl × dl, k=1,…,n, i=1,…,m
and
x  Rn.
Rn. x
x ∞. Default = 1000.
∞. Default = 1000. Rn, A
Rn, A  Rml × n, bL,bU
Rml × n, bL,bU
 Rml and Qk(i) are sparse or dense symmetric matrices.
The matrix sizes may vary between different linear matrix inequalities
(LMI) but must be the same in each particular constraint.
Rml and Qk(i) are sparse or dense symmetric matrices.
The matrix sizes may vary between different linear matrix inequalities
(LMI) but must be the same in each particular constraint.















































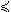 0
0