« Previous « Start » Next »
6 MINOS details
6.1 Introduction
TOMLAB /MINOS (hereafter referred to as MINOS) is a linear and
nonlinear programming system, designed to solve large-scale
constrained optimization problems of the following form:
|
|
|
|
F(x) + cT x + dT y |
|
| s/t |
b1 |
< f(x) + A1 y < |
b2 |
| |
b3 |
< A2x + A3 y < |
b4 |
| |
l |
< (x, y) < |
u |
|
(31) |
where the vectors
bi,
c,
d,
l,
u and the matrices
Ai
are constant,
F(
x) is a nonlinear function of some of the
variables, and
f(
x) is a vector of nonlinear functions. The
nonlinearities (if present) may be of a general nature but must be
smooth and preferably “almost linear", in the sense that they
should not change radically with small changes in the variables. We
make the following definitions:
| x |
the nonlinear variables |
| y |
the linear variables |
| (x, y) |
the vector x y |
| (1.1) |
the objective function |
| (1.2) |
the nonlinear constraints |
| (1.3) |
the linear constraints |
| (1.4) |
the bounds on the variables |
| m |
the total number of general constraints in (2) and (3) |
| n |
the total number of variables in x and y |
| m1 |
the number of nonlinear constraints (the dimension of f(x)) |
| n1 |
the number of nonlinear variables (the dimension of x) |
| n1′ |
the number of nonlinear objective variables (in F(x)) |
| n1′′ |
the number of nonlinear Jacobian variables (in f(x)) |
A large-scale problem is one in which
m and
n are several
hundred or several thousand. MINOS takes advantage of the fact
that the constraint matrices
Ai and the partial derivatives
∂
fi(
x) / ∂
xj are typically sparse (contain many
zeros).
The dimensions
n1′ and
n1′′ allow for the fact that
F(
x)
and
f(
x) may involve different sets of nonlinear variables “
x".
The two sets of variables
always overlap, in the sense that
the shorter “
x" is always the same as the beginning of the other.
If
x is the same in both cases, we have
n1 =
n1′ =
n1′′.
Otherwise, we define the number of nonlinear variables to be
n1 =
max(
n1′,
n1′′).
In the following sections we introduce more terminology and give an
overview of the MINOS optimization algorithms and the main system
features.
6.1.1 Linear Programming
When
F(
x) and
f(
x) are absent, the problem becomes a
linear program. Since there is no need to distinguish between
linear and nonlinear variables, we use
x rather than
y. We also
convert all general constraints into equalities with the aid of
slack variables
s, so that the only inequalities are simple bounds
on the variables. Thus, we write linear programs in the form
| |
|
|
cT x subject to Ax + s = b,
l ≤ (x, s) ≤ u.
(32) |
When the constraints are linear, the bounds on the slacks are
defined so that
b = 0. When there are nonlinear constraints, some
elements of
b are nonzero.
In the mathematical programming world,
x and
s are sometimes
called
structural variables and
logical variables.
Their upper and lower bounds are fundamental to problem formulations
and solution algorithms. Some of the components of
l may be
−∞ and those of
u may be +∞. If
lj =
uj, a
variable is said to be
fixed, and if its bounds are −∞
and +∞, the variable is called
free.
Within MINOS, a point (
x,
s) is said to be
feasible if the
following are true:
-
The constraints Ax + s = b are satisfied to within
machine precision ≈ 10−15.
- The bounds l ≤ (x, s) ≤ u are satisfied to within a
feasibility tolerance δfea ≈ 10−6.
- The nonlinear constraints (31) are satisfied to within a
row tolerance δrow ≈ 10−6.
Tolerances such as δ
fea and δ
row may be specified by
setting
Feasibility tolerance and
Row tolerance.
MINOS solves linear programs using a reliable implementation of
the
primal simplex method,
in which the
constraints
Ax +
s =
b are partitioned into the form
where the
basis matrix B is a square and nonsingular
submatrix of (
A I ). The elements of
x B and
x N are called the
basic and nonbasic variables respectively. Together, they are a
permutation of the vector (
x,
s). Certain
dual variables
π and
reduced costs d N are defined by the equations
BTπ =
c B,
d N =
c N −
NTπ,
(34)
where (
c B,
c N) is a permutation of the objective vector (
c,
0).
At a feasible point, nonbasic variables are typically equal to one
of their bounds, and basic variables are somewhere between their
bounds. To reach an optimal solution, the simplex method performs a
sequence of
iterations of the following general nature. With
guidance from
d N, a nonbasic variable is chosen to move from its
current value, and the basic variables are adjusted to satisfy the
constraints in (
32). Usually one of the basic variables
reaches a bound. The basis partition is then redefined with a column
of
B being replaced by a column of
N. When no such interchange
can be found to reduce the value of
cT x, the current solution is
optimal.
The simplex method
For convenience, let
x denote the variables (
x,
s). The main
steps in a simplex iteration are as follows:
-
Compute dual variables:
-
Solve BTπ = c B.
- Price:
-
Compute some or all of the reduced costs d N = c N − NTπ
to determine if a favorable nonbasic column aq exists.
- Compute search direction:
-
Solve Bp B = ± aq to determine the basic components of a
search direction p along which the objective is improved.
(The nonbasic elements of p are p N = 0, except for ± 1
for the element corresponding to aq.)
- Find maximum steplength:
-
Find the largest steplength αmax such that
x + αmax p continues to
satisfy the bounds on the variables. The steplength may be
determined by the new nonbasic variable reaching its opposite
bound, but normally some basic variable will reach a bound first.
- Update:
-
Take the step αmax. If this was determined by a
basic variable, interchange the corresponding column
of B with column aq from N.
When a starting basis is chosen and the basic variables
x B are
first computed, if any components of
x B lie significantly outside
their bounds, we say that the current point is
infeasible. In
this case, the simplex method uses a “Phase 1" procedure to reduce
the sum of infeasibilities. This is similar to the subsequent
“Phase 2" procedure just described.
The feasibility tolerance δ
fea is used to determine which Phase
is in effect. A similar
optimality tolerance δ
opt is
used during pricing to judge whether any reduced costs are
significantly large. (This tolerance is scaled by

π

, a
measure of the size of the current π.)
If the solution procedures are interrupted, some of the nonbasic
variables may lie strictly
between their bounds:
lj <
xj <
uj. In addition, at a “feasible" or “optimal" solution, some of
the basic variables may lie slightly outside their bounds:
lj −
δ
fea ≤
xj ≤
uj + δ
fea. In rare cases, even a few
nonbasic variables might lie outside their bounds by as much as
δ
fea.
MINOS maintains a sparse
LU factorization of the basis matrix
B, using a Markowitz ordering scheme and Bartels-Golub updates, as
implemented in the Fortran package
LUSOL
The basis factorization is central
to the efficient handling of sparse linear and nonlinear
constraints.
6.1.2 Problems with a Nonlinear Objective
When nonlinearities are confined to the term
F(
x) in the objective
function, the problem is a linearly constrained nonlinear program.
MINOS solves such problems using a
reduced-gradient method
combined with a
quasi-Newton method
that generally leads to superlinear convergence.
The implementation follows that described in
Murtagh and Saunders.
As a slight generalization of (
33), the constraints
Ax +
s
=
b are partitioned into the form
Bx B +
Sx S +
Nx N =
b,
(35)
where
x S is a set of
superbasic variables. As before, the
nonbasic variables are normally equal to one of their bounds, while
the basic
and superbasic variables lie somewhere between
their bounds (to within δ
fea). Let the number of superbasic
variables be
n S, the number of columns in
S. At a solution,
n S will be no more than
n1, the number of nonlinear variables,
and it is often much smaller than this. In many real-life cases we
have found that
n S remains reasonably small, say 200 or less,
regardless of the size of the problem. This is one reason why
MINOS has proved to be a practical tool.
In the reduced-gradient method,
x S is regarded as a set of
“independent variables" that are allowed to move in any desirable
direction to reduce the objective function (or the sum of
infeasibilities). The basic variables are then adjusted in order to
continue satisfying the linear constraints. If it appears that no
improvement can be made with the current definition of
B,
S and
N, one of the nonbasic variables is selected to be added to
S,
and the process is repeated with an increased value of
n S. At all
stages, if a basic or superbasic variable encounters one of its
bounds, that variable is made nonbasic and the value of
n S is
reduced by one.
For linear programs, we may interpret the simplex method as being
the same as the reduced-gradient method, with the number of
superbasic variables oscillating between 0 and 1. (In general, a
step of the simplex method
or the reduced-gradient method is
called a
minor iteration.)
A certain matrix
Z is needed for descriptive purposes. It takes
the form
though it is never computed explicitly. Given
LU factors of the
basis matrix
B, it is possible to compute products of the form
Z
q and
ZT g by solving linear equations involving
B or
BT.
This in turn allows optimization to be performed on the superbasic
variables, while the basic variables are adjusted to satisfy the
general linear constraints. (In the description below, the
reduced-gradient vector satisfies
d S =
ZT g, and the search
direction satisfies
p =
Zp S.)
An important part of MINOS is the quasi-Newton method used to
optimize the superbasic variables. This can achieve superlinear
convergence during any sequence of iterations for which the
B,
S,
N partition remains constant. It requires a dense
upper-triangular matrix
R of dimension
n S, which is updated in
various ways to approximate the
reduced Hessian:
where
H is the
Hessian of the objective function, i.e. the
matrix of second derivatives of
F(
x). As for unconstrained
optimization, the storage required for
R is sometimes a limiting
factor.
The reduced-gradient method
Let
g be the gradient of the nonlinear objective (
31).
The main steps in a reduced-gradient iteration are as follows:
-
Compute dual variables and reduced gradient:
-
Solve BTπ = g B and compute the reduced-gradient vector
d S = g S − STπ.
- Price:
-
If
 d S
d S is sufficiently small,
compute some or all of the reduced costs d N = g N − NTπ
to determine if a favorable nonbasic column aq exists.
If so, move that column from N into S, expanding R accordingly.
is sufficiently small,
compute some or all of the reduced costs d N = g N − NTπ
to determine if a favorable nonbasic column aq exists.
If so, move that column from N into S, expanding R accordingly.
- Compute search direction:
-
Solve RT R p S = − d S and Bp B = − Sp S
to determine the superbasic and basic components of a
search direction p along which the objective is improved.
(The nonbasic elements of p are p N = 0.)
- Find maximum steplength:
-
Find the largest steplength αmax such that
x + αmax p continues to
satisfy the bounds on the variables.
- Perform linesearch:
-
Find an approximate solution to the one-dimensional problem
|
F(x+α p)
subject to 0 ≤ α ≤ αmax.
|
- Update (quasi-Newton):
-
Take the step α. Apply a quasi-Newton update to R
to account for this step.
- Update (basis change):
-
If a superbasic variable reached a bound, move it from S into N.
If a basic variable reached a bound, find a suitable
superbasic variable to move from S into B,
and move the basic variable into N.
Update R if necessary.
At an optimum, the reduced gradient
d S should be zero. MINOS
terminates when
 d S
d S
≤ δ
opt
π

and the reduced
costs (component of
d N) are all sufficiently positive or
negative, as judged by the same quantity δ
opt
π

.
In the linesearch,
F(
x+α
p) really means the objective
function (
31) evaluated at the point (
x,
y,
s) + α
p. This steplength procedure is another important part of MINOS.
Two different procedures are used, depending on whether or not all
gradients are known
analytically.
The
number of nonlinear function evaluations required may be influenced
by setting the
Linesearch tolerance in the SPECS file.
Normally, the objective function
F(
x) will never be evaluated at a
point
x unless that point satisfies the linear constraints and the
bounds on the variables. An exception is during a finite-difference
check on the calculation of gradient elements. This check is
performed at the
starting point x0, which takes default
values or may be specified. MINOS ensures that the bounds
l ≤
x0 ≤
u are satisfied, but in general the starting point will not
satisfy the general linear constraints. If
F(
x0) is undefined,
the gradient check should be suppressed (
Verify level -1), or
the starting point should be redefined.
6.1.3 Problems with Nonlinear Constraints
If any of the constraints are nonlinear, MINOS employs a
projected Lagrangian algorithm, based on a method due to
Robinson, see Murtagh and Saunders.
This
involves a sequence of
major iterations, each of which
requires the solution of a
linearly constrained subproblem.
Each subproblem contains linearized versions of the nonlinear
constraints, as well as the original linear constraints and bounds.
At the start of the
k-th major iteration, let (
xk,
yk) be an
estimate of the variables, and let λ
k be an estimate of the
Lagrange multipliers (dual variables) associated with the nonlinear
constraints. The constraints are linearized by changing
f(
x) in
Equation (2) to its linear approximation:
f(x, xk) = f(xk) + J(xk)(x − xk),
or more briefly
f =
fk +
Jk(
x −
xk), where
J(
xk) is the
Jacobian matrix evaluated at
xk. (The
i-th row of the
Jacobian is the gradient vector for the
i-th nonlinear constraint
function.) The subproblem to be solved during the
k-th major
iteration is then
|
|
|
| F(x) + cT x + dT y − λkT fd + |
|
ρ  fd fd  2 2 |
|
| s/t b1 |
≤ f+ A1y ≤ |
b2 |
| b3 |
≤ A2x + A3y ≤ |
b4, |
| l |
≤ (x, y) ≤ |
u, |
|
(38) |
where
fd =
f −
f is the difference between
f(
x) and its
linearization. The objective function (
38) is called an
augmented Lagrangian. The scalar ρ
k is a
penalty
parameter, and the term involving ρ
k is a modified
quadratic penalty function.
MINOS uses the reduced-gradient method to solve each subproblem.
As before, slack variables are introduced and the vectors
bi are
incorporated into the bounds on the slacks. The linearized
constraints take the form
We refer to this system as
Ax +
s =
b as in the linear case. The
Jacobian
Jk is treated as a sparse matrix, the same as the
matrices
A1,
A2 and
A3. The quantities
Jk,
b,
λ
k and ρ
k change each major iteration.
The projected Lagrangian method
For convenience, suppose that all variables and constraints are
nonlinear. The main steps in a major iteration are as follows:
-
Solve subproblem:
-
Find an approximate solution (2.8 x, λ) to the
kth subproblem (38)–(38).
- Compute search direction:
-
Adjust the elements of λ if necessary (if they
have the wrong sign).
Define a search direction
(Δ x, Δλ) = (2.8 x − xk, λ − λk).
- Find steplength:
-
Choose a steplength σ such that some merit
function M(x,λ) has a suitable value at the point
(xk + σΔ x, λk + σΔλ).
- Update:
-
Take the step σ to obtain (xk+1, λk+1).
In some cases, adjust ρk.
For the first major iteration, the nonlinear constraints are ignored
and minor iterations are performed until the original linear
constraints are satisfied.
The initial Lagrange multiplier estimate is typically λ
k =
0 (though it can be provided by the user). If a subproblem
terminates early, some elements of the new estimate λ may be
changed to zero.
The penalty parameter initially takes a certain default value
ρ
k = 100.0/
m1, where
m1 is the number of nonlinear
constraints. (A value
r times as big is obtained by specifying
Penalty parameter r.) For later major iterations, ρ
k
is reduced in stages when it appears that the sequence
{
xk,λ
k} is converging. In many cases it is safe to
specify
Penalty parameter 0.0 at the beginning, particularly
if a problem is only mildly nonlinear. This may improve the overall
efficiency.
In the output from MINOS, the term
Feasible subproblem
indicates that the
linearized constraints
(
38)–(
38) have been satisfied. In general, the
nonlinear constraints are satisfied only in the limit, so that
feasibility and
optimality occur at essentially the
same time. The nonlinear constraint violation is printed every
major iteration. Even if it is zero early on (say at the initial
point), it may increase and perhaps fluctuate before tending to
zero. On “well behaved" problems, the constraint violation will
decrease quadratically (i.e., very quickly) during the final few
major iterations.
For certain rare classes of problem it is safe to request the values
λ
k = 0 and ρ
k=0 for all subproblems by specifying
Lagrangian = No (in which case the nonlinear constraint
functions are evaluated only once per major iteration). However for
general problems, convergence is much more likely with the default
setting,
Lagrangian = Yes.
The merit function
Unfortunately, it is not known how to define a merit function
M(
x,λ) that can be
reduced at every major iteration.
As a result, there is no guarantee that the projected Lagrangian
method described above will converge from an arbitrary starting
point. This has been the principal theoretical gap in MINOS,
finally resolved by the PhD research of
Michael Friedlander.
The main features needed to stabilize MINOS are:
-
To relax the linearized constraints via an ℓ1 penalty function.
- To repeat a major iteration with increased ρk (and more
relaxed linearized constraints) if the nonlinear constraint
violation would increase too much.
In practice, the method of MINOS 5.51 often does converge and a
good
rate of convergence is often achieved in the final major
iterations, particularly if the constraint functions are “nearly
linear". As a precaution, MINOS prevents radical changes from one
major iteration to the next. Where possible, the steplength is
chosen to be σ = 1, so that each new estimate of the solution
is (
xk+1, λ
k+1) = (2.8
x, λ), the solution of
the subproblem. If this point is “too different", a shorter
steplength σ < 1 is chosen.
If the major iterations for a particular model do not appear to be
converging, some of the following actions may help:
-
Specify initial activity levels for the nonlinear variables
as carefully as possible.
- Include sensible upper and lower bounds on all variables.
- Specify a Major damping parameter that is lower than the
default value. This tends to make σ smaller.
- Specify a Penalty parameter that is higher than the
default value. This tends to prevent excessive departures
from the constraint linearization.
6.1.4 Problem Formulation
In general, it is worthwhile expending considerable prior analysis
to make the constraints completely linear if at all possible.
Sometimes a simple transformation will suffice. For example, a
pipeline optimization problem has pressure drop constraints of the
form
|
+ |
|
+ 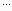 ≤
PT2 − P02, ≤
PT2 − P02,
|
where
di are the design variables (pipe diameters) and the other
terms are constant. These constraints are highly nonlinear, but by
redefining the decision variables to be
xi = 1/
di4.814 we can
make the constraints linear. Even if the objective function becomes
more nonlinear by such a transformation (and this usually happens),
the advantages of having linear constraints greatly outweigh this.
Similarly, it is usually best not to move nonlinearities from the
objective function into the constraints. For example, we should
not replace “
minimize F(
x)" by
minimize z subject to F(x) − z = 0.
Scaling is a very important matter during problem formulation.
A general rule is to scale both the data and the variables to be as
close to 1.0 as possible. In general we suggest the range 1.0 to
10.0. When conflicts arise, one should sacrifice the objective
function in favor of the constraints. Real-world problems tend to
have a natural scaling within each constraint, as long as the
variables are expressed in consistent physical units. Hence it is
often sufficient to apply a scale factor to each row. MINOS has
options to scale the rows and columns of the constraint matrix
automatically. By default, only the linear rows and columns are
scaled, and the procedure is reliable. If you request that the
nonlinear constraints and variables be scaled, bear in mind that the
scale factors are determined by the initial Jacobian
J(
x0), which
may differ considerably from
J(
x) at a solution.
Finally,
upper and lower bounds on the variables (and on the
constraints) are extremely useful for confining the region over
which optimization has to be performed. If sensible values are
known, they should always be used. They are also important for
avoiding singularities in the nonlinear functions. Note that bounds
may be violated slightly by as much as the feasibility tolerance
δ
fea. Hence, if √
x2 or log
x2 appear (for
example) and if δ
fea = 10
−6, the lower bound on
x2 would
normally have to be at least 10
−5. If it is
known that
x2 will be at least 0.5 (say) at a solution, then its lower bound
should be 0.5.
For a detailed discussion of many aspects of numerical optimization,
see
Gill, Murray and Wright for much invaluable advice on problem
formulation and assessment of results.
6.1.5 Restrictions
MINOS is designed to find solutions that are
locally
optimal. The nonlinear functions in a problem must be
smooth (i.e., their first derivatives must exist), especially
near the desired solution. The functions need not be separable.
A certain “feasible" region is defined by the general constraints
and the bounds on the variables. If the objective is convex within
this region and if the feasible region itself is convex, any optimal
solution obtained will be a
global optimum. Otherwise there
may be several local optima, and some of these may not be global.
In such cases the chances of finding a global optimum are usually
increased by choosing a starting point that is “sufficiently
close", but there is no general procedure for determining what
“close" means, or for verifying that a given local optimum is
indeed global.
Integer restrictions cannot be imposed directly. If a variable
xj is required to be 0 or 1, a common ploy is to include a
quadratic term
xj(1 −
xj) in the objective function. MINOS
will indeed terminate with
xj = 0 or 1, but inevitably the final
solution will just be a local optimum. (Note that the quadratic is
negative definite. MINOS will find a global minimum for quadratic
functions that are positive definite or positive semidefinite,
assuming the constraints are linear.)
6.2 Solver Options
The following sections describes some of the solver options
depending on problem type.
6.2.1 Options for Linear Programming
The following options apply specifically to linear programs.
|
|
|
|
|
Crash option |
i |
Default = 3 |
|
Crash tolerance |
t |
Default = 0.1 |
Except on restarts, a Crash procedure is used to select an initial
basis from certain rows and columns of the constraint matrix (
A I ).
The
Crash option i determines which rows and columns of
A
are eligible initially, and how many times Crash is called. Columns
of
I are used to pad the basis where necessary.
-
i=0 The initial basis contains only slack variables: B = I.
- 1 Crash is called once, looking for a triangular
basis in all rows and columns of A.
- 2 Crash is called twice (if there are nonlinear constraints).
The first call looks for a triangular basis in linear rows,
and the first major iteration proceeds with simplex iterations
until the linear constraints are satisfied.
The Jacobian is then evaluated for the second major iteration
and Crash is called again to find a triangular basis in the
nonlinear rows (retaining the current basis for linear
rows).
- 3 Crash is called up to three times
(if there are nonlinear constraints).
The first two calls treat linear equalities and
linear inequalities separately. As before, the last
call treats nonlinear rows at the start of the second major
iteration.
If
i ≥ 1, certain slacks on inequality rows are selected for the
basis first. (If
i ≥ 2, numerical values are used to exclude
slacks that are close to a bound.) Crash then makes several passes
through the columns of
A, searching for a basis matrix that is
essentially triangular. A column is assigned to “pivot" on a
particular row if the column contains a suitably large element in a
row that has not yet been assigned. (The pivot elements ultimately
form the diagonals of the triangular basis.) For remaining
unassigned rows, slack variables are inserted to complete the basis.
The
Crash tolerance allows Crash to ignore certain “small"
nonzeros in each column of
A. If
amax is the largest
element in column
j, other nonzeros
aij in the column are
ignored if |
aij| ≤
amax ×
t. (To be meaningful,
t
should be in the range 0 ≤
t < 1.)
When
t > 0.0, the bases obtained by Crash may not be strictly
triangular, but are likely to be nonsingular and almost triangular.
The intention is to choose a basis containing more columns of
A
and fewer (arbitrary) slacks. A feasible solution may be reached
sooner on some problems.
For example, suppose the first
m columns of
A are the matrix
shown under
LU factor tolerance; i.e., a tridiagonal matrix
with entries −1, 4, −1. To help Crash choose all
m columns for
the initial basis, we would specify
Crash tolerance t for
some value of
t > 1/4.
6.2.2 Options for All Problems
The following options have the same purpose for all problems,
whether they linear or nonlinear.
|
|
|
|
|
Check frequency |
k |
Default = 60 |
Every
k-th minor iteration after the most recent basis
factorization, a numerical test is made to see if the current
solution
x satisfies the general linear constraints (including
linearized nonlinear constraints, if any). The constraints are of
the form
Ax +
s =
b, where
s is the set of slack variables. To
perform the numerical test, the residual vector
r =
b −
Ax −
s is
computed. If the largest component of
r is judged to be too large,
the current basis is refactorized and the basic variables are
recomputed to satisfy the general constraints more accurately.
Check frequency 1 is useful for debugging purposes, but
otherwise this option should not be needed.
|
|
|
|
|
Cycle limit |
l |
Default = 1 |
|
Cycle print |
p |
Default = 1 |
|
Cycle tolerance |
t |
Default = 0.0 |
|
Phantom columns |
c |
Default = 0 |
|
Phantom elements |
e |
Default = 0 |
|
|
|
|
|
Debug level |
l |
Default = 0 |
This causes various amounts of information to be output to the Print
file. Most debug levels are not helpful to normal users, but they
are listed here for completeness.
-
l = 0
- No debug output.
- l = 2
- (or more) Output from m5setx showing the maximum
residual after a row check.
- l = 40
- Output from lu8rpc (which updates the LU factors
of the basis matrix), showing the position of the
last nonzero in the transformed incoming column.
- l = 50
- Output from lu1mar (which computes the LU factors
each refactorization), showing each pivot row and column
and the dimensions of the dense matrix involved in the associated
elimination.
- l = 100
- Output from m2bfac and m5log listing the basic
and superbasic variables and their values at every iteration.
|
|
|
|
|
Expand frequency |
k |
Default = 10000 |
This option is part of an anti-cycling procedure designed to
guarantee progress even on highly degenerate problems.
“Cycling" can occur only if zero steplengths are allowed. Here, the
strategy is to force a positive step at every iteration, at the
expense of violating the bounds on the variables by a small amount.
Suppose that the
Feasibility tolerance is δ. Over a
period of
k iterations, the tolerance actually used by MINOS
increases from 0.5δ to δ (in steps of 0.5δ/
k).
Every
k iterations, or when feasibility and optimality are first
detected, a resetting procedure eliminates any infeasible nonbasic
variables. Some additional iterations may be needed to restore
feasibility and optimality. Increasing
k reduces that likelihood,
but it gives less freedom to choose large pivot elements during
basis changes. (See
Pivot tolerance.)
|
|
|
|
|
Factorization frequency |
k |
Default = 100 (LP) or 50
(NLP) |
With linear programs, most iterations cause a basis change, in which
one column of the basis matrix
B is replaced by another. The
LU
factors of
B must be updated accordingly. At most
k updates are
performed before the current
B is factorized directly.
Each update tends to add nonzeros to the
LU factors. Since the
updating method is stable,
k mainly affects the efficiency of
minor iterations, rather than stability.
High values of
k (such as 100 or 200) may be more efficient on
“dense" problems, when the factors of
B tend to have two or three
times as many nonzeros as
B itself. Lower values of
k may be
more efficient on problems that are very sparse.
|
|
|
|
|
Feasibility tolerance |
t |
Default = 1.0e-6 |
This sets the feasibility tolerance δ
fea =
t (see
§
6.2.1). A variable or constraint is considered
feasible if it does not lie outside its bounds by more than
δ
fea.
MINOS first attempts to satisfy the linear constraints and bounds.
If the sum of infeasibilities cannot be reduced to zero, the problem
is declared infeasible. Let
sinf be the corresponding sum of
infeasibilities. If
sinf is quite small, it may be appropriate to
raise
t by a factor of 10 or 100. Otherwise, some error in the
data should be suspected. If
sinf is not small, there may be other
points that have a significantly smaller sum of infeasibilities.
MINOS does not attempt to find a solution that minimizes the sum.
For
Scale option 1 or 2, feasibility is defined in terms of
the
scaled problem (since it is then more likely to be
meaningful). The final unscaled solution can therefore be infeasible
by an unpredictable amount, depending on the size of the scale
factors. Precautions are taken so that in a “feasible solution" the
original variables will never be infeasible by more than 0.1.
Values that large are very unlikely.
|
|
|
|
|
Iterations limit |
k |
Default = 3m |
MINOS stops after
k iterations even if the simplex method has
not yet reached a solution. If
k = 0, no iterations are performed,
but the starting point is tested for both feasibility and
optimality.
|
|
|
|
|
LU factor tolerance |
t1 |
Default = 100.0 (LP) or 5.0 (NLP) |
|
LU update tolerance |
t2 |
Default = 110.0 (LP)
or 5.0 (NLP) |
These tolerances affect the stability and sparsity of the basis
factorization
B =
LU during refactorization and updating,
respectively. They must satisfy
t1,
t2 ≥ 1.0. The matrix
L
is a product of matrices of the form
where the multipliers μ satisfy |μ| ≤
ti. Values near
1.0 favor stability, while larger values favor sparsity. The default
values usually strike a good compromise. For large and relatively
dense problems,
t1 = 10.0 or 5.0 (say) may give a useful
improvement in stability without impairing sparsity to a serious
degree.
For certain very regular structures (e.g., band matrices) it may be
necessary to reduce
t1 and/or
t2 in order to achieve
stability. For example, if the columns of
A include a submatrix
of the form





 |
|
| 4 |
−1 |
| −1 |
4 |
−1 |
| |
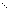 |
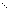 |
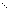 |
| |
|
−1 |
4 |
−1 |
| |
|
|
−1 |
4 |
|
|





 |
, |
one should set both
t1 and
t2 to values in the range
1.0 ≤
ti < 4.0.
|
|
|
|
|
LU density tolerance |
t3 |
Default = 0.5 |
|
LU singularity tolerance |
t4 |
Default = є0.67
≈ 3.25e−11 |
The density tolerance
t3 is used during
LU factorization of
the basis matrix. Columns of
L and rows of
U are formed
one at a time, and the remaining rows and columns of the
basis are altered appropriately. At any stage, if the density
of the remaining matrix exceeds
t3,
the Markowitz strategy for choosing pivots is altered to
reduce the time spent searching for each remaining pivot.
Raising the density tolerance towards 1.0 may give slightly
sparser
LU factors, with a slight increase in factorization time.
The singularity tolerance
t4 helps guard against ill-conditioned
basis matrices. When the basis is refactorized, the diagonal
elements of
U are tested as follows: if |
Ujj| ≤
t4 or
|
Ujj| <
t4 max
i |
Uij|, the
j-th column of the basis is
replaced by the corresponding slack variable. (This is most likely
to occur after a restart, or at the start of a major iteration.)
In some cases, the Jacobian matrix may converge to values that make
the basis exactly singular. (For example, a whole row of the
Jacobian could be zero at an optimal solution.) Before exact
singularity occurs, the basis could become very ill-conditioned and
the optimization could progress very slowly (if at all). Setting
t4 =
1.0e-5, say, may help cause a judicious change of
basis.
|
|
|
|
|
Maximize |
|
Minimize |
|
Default |
This specifies the required direction of optimization.
|
|
|
|
|
Multiple price |
k |
Default = 1 |
It is not normal to set
k>1 for linear programs, as it causes
MINOS to use the reduced-gradient method rather than the simplex
method. The number of iterations, and the total work, are likely to
increase.
The reduced-gradient iterations do
not correspond to the very
efficient multiple pricing “minor iterations" carried out by
certain commercial linear programming systems. Such systems require
storage for
k dense vectors of dimension
m, so that
k is
usually limited to 5 or 6. In MINOS, the total storage requirements
increase only slightly with
k. (The
Superbasics limit must
be at least
k.)
|
|
|
|
|
Optimality tolerance |
t |
Default = 1.0e-6 |
This is used to judge the size of the reduced gradients
dj =
gj −
π
T aj, where
gj is the gradient of the objective function
corresponding to the
j-th variable,
aj is the associated column
of the constraint matrix (or Jacobian), and π is the set of dual
variables.
By construction, the reduced gradients for basic variables are
always zero. Optimality is declared if the reduced gradients for
nonbasic variables at their lower or upper bounds satisfy
dj /

π

≥ −
t or
dj /

π

≤
t respectively, and if
|
dj| /

π

≤
t for superbasic variables.
In those tests,

π

is a measure of the size of the dual
variables. It is included to make the tests independent of a large
scale factor on the objective function. The quantity actually used
is defined by σ = Σ
i=1m |π
i|,

π

=
max{σ / √
m, 1.0} , so that only scale factors larger
than 1.0 are allowed for. If the objective is scaled down to be very
small, the optimality test reduces to comparing
dj against
t.
|
|
|
|
|
Partial price |
p |
Default = 10 (LP) or 1 (NLP) |
This parameter is recommended for large problems that have
significantly more variables than constraints. It reduces the work
required for each “pricing" operation (when a nonbasic variable is
selected to become basic or superbasic).
When
p=1, all columns of the constraint matrix (
A I ) are searched.
Otherwise,
A and
I are partitioned to give
p roughly equal
segments
Aj,
Ij (
j = 1 to
p). If the previous pricing
search was successful on
Aj,
Ij, the next search begins on
the segments
Aj+1,
Ij+1. (Subscripts are modulo
p.)
If a reduced gradient is found that is larger than some dynamic
tolerance, the variable with the largest such reduced gradient (of
appropriate sign) is selected to become superbasic. (Several may be
selected if multiple pricing has been specified.) If nothing is
found, the search continues on the next segments
Aj+2,
Ij+2, and so on.
Partial price t (or
t/2 or
t/3) may be appropriate for
time-stage models having
t time periods.
|
|
|
|
|
Pivot tolerance |
t |
Default = є2/3 ≈
10−11 |
Broadly speaking, the pivot tolerance is used to prevent columns
entering the basis if they would cause the basis to become almost
singular. When
x changes to
x + α
p for some search
direction
p, a “ratio test" is used to determine which component
of
x reaches an upper or lower bound first. The corresponding
element of
p is called the pivot element.
For linear problems, elements of
p are ignored (and therefore
cannot be pivot elements) if they are smaller than the pivot
tolerance
t. For nonlinear problems, elements smaller than
t p
p
are ignored.
It is common for two or more variables to reach a bound at
essentially the same time. In such cases, the
Feasibility
tolerance provides some freedom to maximize the pivot element and
thereby improve numerical stability. Excessively small Feasibility
tolerances should therefore not be specified.
To a lesser extent, the
Expand frequency also provides some
freedom to maximize the pivot element. Excessively
large
Expand frequencies should therefore not be specified.
|
|
|
|
|
Scale option |
l |
Default = 2 (LP) or 1 (NLP) |
|
Scale |
Yes |
|
Scale |
No |
|
Scale linear variables |
|
Same as Scale option 1 |
|
Scale nonlinear variables |
|
Same as Scale option 2 |
|
Scale all variables |
|
Same as Scale option 2 |
|
Scale tolerance |
t |
Default = 0.9 |
|
Scale, Print |
|
Scale, Print, Tolerance |
t |
Three scale options are available as follows:
-
l = 0
- No scaling. If storage is at a premium, this option
saves m+n words of workspace.
- l = 1
- Linear constraints and variables are scaled by an
iterative procedure that attempts to make the
matrix coefficients as close as possible to 1.0 (see
Fourer, 1982). This sometimes improves the performance
of the solution procedures.
- l = 2
- All constraints and variables are scaled by the iterative
procedure. Also, a certain additional scaling is performed
that may be helpful if the right-hand side b or the
solution x is large. This takes into
account columns of ( A I ) that are fixed or have positive
lower bounds or negative upper bounds.
Scale Yes sets the default scaling. (
Caution: If all
variables are nonlinear,
Scale Yes unexpectedly does
nothing, because there are no linear variables to scale.)
Scale No suppresses scaling (equivalent to
Scale option
0).
If nonlinear constraints are present,
Scale option 1 or
0 should generally be tried at first.
Scale option 2 gives
scales that depend on the initial Jacobian, and should therefore be
used only if (a) a good starting point is provided, and (b) the
problem is not highly nonlinear.
Scale, Print causes the row-scales
r(
i) and column-scales
c(
j) to be printed. The scaled matrix coefficients are
aij =
aij c(
j) /
r(
i), and the scaled bounds on the
variables and slacks are
lj =
lj /
c(
j),
uj =
uj /
c(
j),
where
c(
j) ≡
r(
j−
n) if
j>
n.
All forms except
Scale option may specify a tolerance
t,
where 0 <
t < 1 (for example:
Scale, Print, Tolerance =
0.99). This affects how many passes might be needed through the
constraint matrix. On each pass, the scaling procedure computes the
ratio of the largest and smallest nonzero coefficients in each
column:
| ρj = |
|
|aij| / |
|
|aij| (aij≠ 0). |
If max
j ρ
j is less than
t times its previous value,
another scaling pass is performed to adjust the row and column
scales. Raising
t from 0.9 to 0.99 (say) usually increases the
number of scaling passes through
A. At most 10 passes are made.
If a
Scale option has not already been specified,
Scale,
Print or
Scale tolerance both set the default scaling.
|
|
|
|
|
Weight on linear objective |
w |
Default = 0.0 |
This keyword invokes the so-called
composite objective
technique, if the first solution obtained is infeasible, and if the
objective function contains linear terms. While trying to reduce the
sum of infeasibilities, the method also attempts to optimize the
linear objective. At each infeasible iteration, the objective
function is defined to be
|
σ w(cT x) + (sum of infeasibilities), |
where σ=1 for minimization, σ= −1 for maximization,
and
c is the linear objective. If an “optimal" solution is
reached while still infeasible,
w is reduced by a factor of 10.
This helps to allow for the possibility that the initial
w is too
large. It also provides dynamic allowance for the fact that the sum
of infeasibilities is tending towards zero.
The effect of
w is disabled after 5 such reductions, or if a
feasible solution is obtained.
The
Weight option is intended mainly for linear programs. It is
unlikely to be helpful on nonlinear problems.
6.2.3 Options for Nonlinear Objectives
The following options apply to nonlinear programs whose constraints
are linear.
|
|
|
|
|
Crash option |
l |
Default = 3 |
|
Crash tolerance |
t |
Default = 0.1 |
These options are the same as for linear programs.
6.2.4 Options for All Nonlinear problems
|
|
|
|
|
Expand frequency |
k |
Default = 10000 |
This option is used the same as for linear programs, but takes
effect only when there is just one superbasic variable. (Cycling can
occur only when the current solution is at a vertex of the feasible
region. Thus, zero steps are allowed if there is more than one
superbasic variable, but otherwise positive steps are enforced.)
Increasing
k helps reduce the number of slightly infeasible
nonbasic basic variables (most of which are eliminated during a
resetting procedure). However, it also diminishes the freedom to
choose a large pivot element (see
Pivot tolerance).
|
|
|
|
|
Feasibility tolerance |
t |
Default = 1.0e-6 |
When the constraints are linear, a
feasible solution is one
in which all variables, including slacks, satisfy their upper and
lower bounds to within the absolute tolerance
t. (Since slacks
are included, this means that the general linear constraints are
also satisfied to within
t.)
When nonlinear constraints are present, a
feasible
subproblem is one in which the linear constraints and bounds, as
well as the current linearization of the nonlinear constraints, are
satisfied to within the tolerance
t.
MINOS first attempts to satisfy the linear constraints and bounds.
If the sum of infeasibilities cannot be reduced to zero, the problem
is declared infeasible.
Normally, the nonlinear functions
F(
x) and
f(
x) are evaluated
only at points
x that satisfy the linear constraints and bounds.
If the functions are undefined in certain regions, every attempt
should be made to eliminate these regions from the problem. For
example, for a function
F(
x) = √
x1 + log
x2, it would be
essential to place lower bounds on both variables. If
Feasibility tolerance = 10
−6, the bounds
x1 ≥ 10
−5 and
x2 ≥ 10
−4 might be appropriate. (The log singularity is
more serious; in general, keep variables as far away from
singularities as possible.)
An exception is during optional gradient checking (see
Verify), which occurs before any optimization takes place. The
points at which the functions are evaluated satisfy the bounds but
not necessarily the general constraints. If this causes difficulty,
gradient checking should be suppressed by setting
Verify level
-1.
If a subproblem is infeasible, the bounds on the linearized
constraints are relaxed in several stages until the subproblem
appears feasible. (The true bounds are restored for the next
subproblem.) This approach sometimes allows the optimization to
proceed successfully. In general, infeasible subproblems are a
symptom of difficulty and it may be necessary to increase the
Penalty parameter or alter the starting point.
Note: Feasibility with respect to the nonlinear constraints
is measured against the
Row tolerance, not the
Feasibility tolerance.
|
|
|
|
|
Hessian dimension |
r |
Default = 50 |
This specifies that an
r ×
r triangular matrix
R is to be
available for use by the quasi-Newton algorithm (to approximate the
reduced Hessian matrix according to
ZT H Z ≈
RT R).
Suppose there are
s superbasic variables at a particular
iteration.
Whenever possible, r should be greater than s.
If
r ≥
s, the first
s columns of
R are used to approximate
the reduced Hessian in the normal manner. If there are no further
changes to the set of superbasic variables, the rate of convergence
is usually superlinear. If
r<
s, a matrix of the form
is used to approximate the reduced Hessian, where
Rr is an
r×
r upper triangular matrix and
D is a
diagonal
matrix of order
s−
r. The rate of convergence is no longer
superlinear (and may be arbitrarily slow).
The storage required is of order 1/2
r2, which is
substantial if
r is as large as 1000 (say). In general,
r
should be a slight over-estimate of the final number of superbasic
variables, whenever storage permits. It need not be larger than
n1 + 1, where
n1 is the number of nonlinear variables. For
many problems it can be much smaller than
n1.
|
|
|
|
|
Iterations limit |
k |
Default = 3m + 10n1 |
If the constraints are linear, this is the maximum number of
iterations allowed for the simplex method or the reduced-gradient
method. Otherwise, it is the maximum number of
minor
iterations, summed over all major iterations.
If
k = 0, no minor iterations are performed, but the starting
point is tested for both feasibility and optimality.
|
|
|
|
|
Linesearch tolerance |
t |
Default = 0.1 |
For nonlinear problems, this controls the accuracy with which a
steplength α is located during one-dimensional searches of
the form
|
F(x+α p)
subject to 0 < α ≤ β. |
A linesearch occurs on most minor iterations for which
x is
feasible. (If the constraints are nonlinear, the function being
minimized is the augmented Lagrangian in equation (5).)
The value of
t must satisfy 0.0 ≤
t < 1.0. The default value
t = 0.1 requests a moderately accurate search, and should be
satisfactory in most cases. If the nonlinear functions are cheap to
evaluate, a more accurate search may be appropriate; try
t = 0.01
or
t = 0.001. The number of iterations should decrease, and this
will reduce total run time if there are many linear or nonlinear
constraints. If the nonlinear functions are
expensive to
evaluate, a less accurate search may be appropriate; try
t = 0.5
or perhaps
t = 0.9. (The number of iterations will probably
increase, but the total number of function evaluations may decrease
enough to compensate.)
|
|
|
|
|
LU singularity tolerance |
t3 |
Default =
є0.67
≈ 3.25e−11 |
|
LU swap tolerance |
t4 |
Default = є1/4
≈ 10−4 |
The singularity tolerance
t3 helps guard against ill-conditioned
basis matrices. When the basis is refactorized, the diagonal
elements of
U are tested as follows: if |
Ujj| ≤
t3 or
|
Ujj| <
t3 max
i |
Uij|, the
j-th column of the basis is
replaced by the corresponding slack variable. (This is most likely
to occur after a restart, or at the start of a major iteration.)
In some cases, the Jacobian matrix may converge to values that make
the basis exactly singular. (For example, a whole row of the
Jacobian could be zero at an optimal solution.) Before exact
singularity occurs, the basis could become very ill-conditioned and
the optimization could progress very slowly (if at all). Setting
t3 =
1.0e-5, say, may help cause a judicious change of
basis.
The
LU swap tolerance is somewhat similar but can take effect
more
easily. It is again used only after a basis factorization, and
normally just at the start of a major iteration. If a diagonal
of
U seems to be rather small (as measured by
t4)
relative to the biggest diagonal of
U, a basis change is made
in which the basic variable associated with the small diagonal of
U
is swapped with a carefully chosen superbasic variable (if there
are any). The number of superbasic variables stays the same.
A message is printed to advise that a swap has occurred.
In practice this tends to help problems whose basis is becoming
ill-conditioned. If the number of swaps becomes excessive, set
LU swap tolerance 1.0e-6, say, or perhaps smaller.
|
|
|
|
|
Minor damping parameter |
d |
Default = 2.0 |
This parameter limits the change in
x during a linesearch. It
applies to all nonlinear problems, once a “feasible solution" or
“feasible subproblem" has been found.
A linesearch of the form
minimizeα F(
x+α
p) is
performed over the range 0 < α ≤ β, where β is
the step to the nearest upper or lower bound on
x. Normally, the
first steplength tried is α
1 = min(1,β), but in some
cases, such as
F(
x) =
aebx or
F(
x) =
axb, even a moderate
change in the components of
x can lead to floating-point overflow.
The parameter
d is therefore used to define a limit β =
d(1 +
 x
x
) /
 p
p
, and the first evaluation of
F(
x) is
at the potentially smaller steplength α
1 = min(1, β,
β).
Wherever possible, upper and lower bounds on
x should be used to
prevent evaluation of nonlinear functions at meaningless points. The
Minor damping parameter provides an additional safeguard. The
default value
d = 2.0 should not affect progress on well behaved
problems, but setting
d = 0.1 or 0.01 may be helpful when rapidly
varying functions are present. A “good" starting point may be
required. An important application is to the class of nonlinear
least-squares problems.
In cases where several local optima exist, specifying a small value
for
d may help locate an optimum near the starting point.
|
|
|
|
|
Multiple price |
k |
Default = 1 |
“Pricing" refers to a scan of the current nonbasic variables to
determine if any should be changed from their current value (by
allowing them to become superbasic or basic).
If multiple pricing is in effect, the
k best nonbasic variables
are selected for admission to the superbasic set. (“Best" means
the variables with largest reduced gradients of appropriate sign.)
If partial pricing is also in effect, the
k best variables are
selected from the current partition of
A and
I.
On large nonlinear problems it may help to set
k > 1 if there are
not many superbasic variables at the starting point but many at the
optimal solution.
|
|
|
|
|
Optimality tolerance |
t |
Default = 1.0e-6 |
|
|
|
|
|
Partial price |
p |
Default = 10 (LP) or 1 (NLP) |
This parameter may be useful for large problems that have
significantly more variables than constraints. Larger values reduce
the work required for each “pricing" operation (when a nonbasic
variable is selected to become basic or superbasic).
|
|
|
|
|
Scale option |
l |
Default = 2 (LP) or 1 (NLP) |
|
Scale |
Yes |
|
Scale |
No |
|
Scale linear variables |
|
Same as Scale option 1 |
|
Scale nonlinear variables |
|
Same as Scale option 2 |
|
Scale all variables |
|
Same as Scale option 2 |
|
Scale tolerance |
t |
Default = 0.9 |
|
Scale, Print |
|
Scale, Print, Tolerance |
t |
Three scale options are available as follows:
-
l = 0
- No scaling. If storage is at a premium, this option
saves m+n words of workspace.
- l = 1
- If some of the variables are linear, the constraints
and linear variables are scaled by an
iterative procedure that attempts to make the
matrix coefficients as close as possible to 1.0.
- l = 2
- The constraints and variables are scaled by the iterative
procedure. Also, a certain additional scaling is performed
that may be helpful if the right-hand side b or the
solution x is large. This takes into
account columns of ( A I ) that are fixed or have positive
lower bounds or negative upper bounds.
Scale option 1 is the default for nonlinear problems. (Only
linear variables are scaled.)
Scale Yes sets the default. (
Caution: If all variables
are nonlinear,
Scale Yes unexpectedly does
nothing,
because there are no linear variables to scale.)
Scale No
suppresses scaling (equivalent to
Scale option 0).
The
Scale tolerance and
Scale, Print options are the
same as for linear programs.
|
|
|
|
|
Subspace tolerance |
t |
Default = 0.5 |
This controls the extent to which optimization is confined to the
current set of basic and superbasic variables (Phase 4 iterations),
before one or more nonbasic variables are added to the superbasic
set (Phase 3). The value specified must satisfy 0 <
t ≤ 1.
When a nonbasic variable
xj is made superbasic, the norm of the
reduced-gradient vector (for all superbasics) is recorded. Let this
be
 ZT g0
ZT g0
. (In fact, the norm is |
dj|, the size of the
reduced gradient for the new superbasic variable
xj.)
Subsequent Phase 4 iterations continue at least until the norm of
the reduced-gradient vector satisfies
 ZT g
ZT g
≤
t ×
 ZT g0
ZT g0
. (
 ZT g
ZT g
is the size of the largest
reduced-gradient among the superbasic variables.)
A smaller value of
t is likely to increase the total number of
iterations, but may reduce the number of basis changes. A larger
value such as
t = 0.9 may sometimes lead to improved overall
efficiency, if the number of superbasic variables is substantially
larger at the optimal solution than at the starting point.
Other convergence tests on the change in the function being
minimized and the change in the variables may prolong Phase 4
iterations. This helps to make the overall performance insensitive
to larger values of
t.
|
|
|
|
|
Superbasics limit |
s |
Default = 50 |
This places a limit on the storage allocated for superbasic
variables. Ideally,
s should be set slightly larger than the
“number of degrees of freedom" expected at an optimal solution.
For nonlinear problems, the number of degrees of freedom is often
called the “number of independent variables". Normally,
s need
not be greater than
n1+1, where
n1 is the number of nonlinear
variables. For many problems,
s may be considerably smaller than
n1. This saves storage if
n1 is very large.
If
Hessian dimension r is specified, the default value of
s is the same number (and conversely). This is a safeguard to
ensure superlinear convergence wherever possible. Otherwise, the
default for both
r and
s is 50.
|
|
|
|
|
Unbounded objective value |
r1 |
Default = 1.0e+20 |
|
Unbounded step size |
r2 |
Default = 1.0e+10 |
These parameters are intended to detect unboundedness in nonlinear
problems. During a linesearch of the form
min
α F(
x + α
p) ,
if |
F | exceeds
r1 or if α exceeds
r2, iterations
are terminated with the exit message
Problem is unbounded (or
badly scaled).
If singularities are present, unboundedness in
F(
x) may be
manifested by a floating-point overflow (during the evaluation of
F(
x + α
p)), before the test against
r1 can be made.
Unboundedness in
x is best avoided by placing finite upper and
lower bounds on the variables. See also the
Minor damping
parameter.
|
|
|
|
|
Verify level |
l |
Default = 0 |
|
Verify objective gradients |
|
Same as Verify level 1 |
|
Verify constraint gradients |
|
Same as Verify level 2 |
|
Verify |
|
Same as Verify level 3 |
|
Verify gradients |
|
Same as Verify level 3 |
|
Verify |
Yes |
Same as Verify level 3 |
|
Verify |
No |
Same as Verify level 0 |
These options refer to a check on the gradients computed by your
nonlinear function routines
funobj and
funcon at the starting
point (the initial value of the nonlinear variables
x(*)).
Values output in the gradient array
g(*) are compared with
estimates obtained by finite differences.
-
l = 0
- Only a “cheap" test is performed, requiring
three evaluations of the nonlinear objective (if any) and two
evaluations of the nonlinear constraints.
- l = 1
- A more reliable check is made on each component
of the objective gradient.
- l = 2
- A check is made on each column of the Jacobian matrix
associated with the nonlinear constraints.
- l = 3
- A detailed check is made on both the objective and
the Jacobian.
- l = −1
- No checking is performed. This may be necessary
if the functions are undefined at the starting point.
Verify level 3 is recommended for a new function routine,
particularly if the “cheap" test indicates error. Missing gradients
are not checked (so there is no overhead). If there are many
nonlinear variables, the
Start and
Stop keywords may be used
to limit the check to a subset.
As noted, gradient verification occurs at the starting point, before
a problem is scaled, and before the first basis is factorized. The
bounds on
x will be satisfied, but the general linear constraints
may not. If the nonlinear objective or constraint functions are
undefined, you could initially specify
Objective = NONE
Nonlinear objective variables 0
Major iterations 1
New basis file 11 (say)
Verify level -1
to obtain a point that satisfies the linear constraints, and then
restart with the correct linear and nonlinear objective, along with
Old basis file 11
Verify level 3
6.2.5 Options for Nonlinear Constraints
The following options apply to problems with nonlinear constraints.
|
|
|
|
|
Completion |
Partial |
Default |
|
Completion |
Full |
When there are nonlinear constraints, this determines whether
subproblems should be solved to moderate accuracy (partial
completion), or to full accuracy (full completion). MINOS
implements the option by using two sets of convergence tolerances
for the subproblems.
Use of partial completion may reduce the work during early major
iterations, unless the
Minor iterations limit is active. The
optimal set of basic and superbasic variables will probably be
determined for any given subproblem, but the reduced gradient may be
larger than it would have been with full completion.
An automatic switch to full completion occurs when it appears that
the sequence of major iterations is converging. The switch is made
when the nonlinear constraint error is reduced below 100
* (
Row tolerance), the relative change in λ
k
is 0.1 or less, and the previous subproblem was solved to
optimality.
Full completion tends to give better Lagrange-multiplier estimates.
It may lead to fewer major iterations, but may result in more minor
iterations.
|
|
|
|
|
Crash option |
l |
Default = 3 |
|
Crash tolerance |
t |
Default = 0.1 |
Let
A refer to the linearized constraint matrix.
-
l = 0
- The initial basis contains only slack variables: B = I.
- l = 1
- A is evaluated at the starting point.
Crash is called once, looking for a triangular basis
in all rows and columns of A.
- l = 2
- A is evaluated only after the linear constraints are satisfied.
Crash is called twice. The first call looks
for a triangular basis in linear rows.
The first major iteration proceeds with simplex-type iterations
until the linear constraints are satisfied.
A is then evaluated for the second major iteration
and Crash is called again to find a triangular basis in the
nonlinear rows (retaining the current basis for linear
rows).
- l = 3
- Crash is called three times, treating
linear equalities and linear inequalities separately,
with simplex-type iterations in between.
As before, the last call treats nonlinear rows
at the start of the second major iteration.
|
|
|
|
|
Feasibility tolerance |
t |
Default = 1.0e-6 |
A “feasible subproblem" is one in which the linear constraints and
bounds, as well as the current linearization of the nonlinear
constraints, are satisfied to within
t.
Note that feasibility with respect to the nonlinear constraints is
determined by the
Row tolerance (not the
Feasibility
tolerance).
MINOS first attempts to satisfy the linear constraints and bounds.
If the sum of infeasibilities cannot be reduced to zero, the problem
is declared infeasible.
If
Scale option = 1 or 2, feasibility is defined in terms of
the scaled problem (since it is then more likely to be meaningful).
Normally, the nonlinear functions
F(
x) and
f(
x) are evaluated
only at points
x that satisfy the linear constraints and bounds.
If the functions are undefined in certain regions, every attempt
should be made to eliminate these regions from the problem. For
example, for a function
F(
x) = √
x1 + log
x2, it would be
essential to place lower bounds on both variables. If
Feasibility tolerance = 10
−6, the bounds
x1 ≥ 10
−5 and
x2 ≥ 10
−4 might be appropriate. (The log singularity is
more serious; in general, keep variables as far away from
singularities as possible.)
An exception is during optional gradient checking (see
Verify), which occurs before any optimization takes place. The
points at which the functions are evaluated satisfy the bounds but
not necessarily the general constraints. If this causes difficulty,
gradient checking should be suppressed by setting
Verify level
-1.
If a subproblem is infeasible, the bounds on the linearized
constraints are relaxed in several stages until the subproblem
appears feasible. (The true bounds are restored for the next
subproblem.) This approach sometimes allows the optimization to
proceed successfully. In general, infeasible subproblems are a
symptom of difficulty and it may be necessary to increase the
Penalty parameter or alter the starting point.
|
|
|
|
|
Lagrangian |
Yes |
Default |
|
Lagrangian |
No |
This determines the form of the objective function used for the
linearized subproblems. The default value
Yes is highly
recommended. The
Penalty parameter value is then also
relevant.
If
No is specified, the nonlinear constraint functions are
evaluated only twice per major iteration. Hence this option may be
useful if the nonlinear constraints are very expensive to evaluate.
However, in general there is a great risk that convergence may not
be achieved.
|
|
|
|
|
Major damping parameter |
d |
Default = 2.0 |
This parameter may assist convergence on problems that have highly
nonlinear constraints. It is intended to prevent large relative
changes between subproblem solutions (
xk,λ
k) and
(
xk+1,λ
k+1). For example, the default value 2.0
prevents the relative change in either
xk or λ
k from
exceeding 200 per cent. It will not be active on well behaved
problems. (If all components of
xk or λ
k are small, the
norms of those vectors will not be allowed to increase beyond about
2.0.)
The parameter is used to interpolate between the solutions at the
beginning and end of each major iteration. Thus,
xk+1 and
λ
k+1 are changed to
xk + σ ( xk+1 − xk) and
λk + σ (λk+1 − λk)
for some steplength σ < 1. In the case of nonlinear
equations (where the number of constraints is the same as the number
of variables) this gives a
damped Newton method.
This is a very crude control. If the sequence of major iterations
does not appear to be converging, one should first re-run the
problem with a higher
Penalty parameter (say 2, 4 or 10).
(Skip this re-run in the case of a square system of nonlinear
equations: there are no degrees of freedom and the
Penalty
parameter value has essentially no effect.)
If the subproblem solutions continue to change violently, try
reducing
d to 0.2 or 0.1 (say).
|
|
|
|
|
Major iterations |
k |
Default = 50 |
This is the maximum number of major iterations allowed. It is
intended to guard against an excessive number of linearizations of
the nonlinear constraints, since in some cases the sequence of major
iterations may not converge.
The progress of the major iterations can be best monitored using
Print level 0 (the default).
|
|
|
|
|
Minor iterations |
k |
Default = 40 |
This is the maximum number of minor iterations allowed during a
major iteration,
after the linearized constraints for that
subproblem have been satisfied. (An arbitrary number of minor
iterations may be needed to find a feasible point for each
subproblem.) The
Iterations limit provides an independent
limit on the total minor iterations (across all subproblems).
A moderate value (e.g., 30 ≤
k ≤ 200) prevents excessive
effort being expended on early major iterations, but allows later
subproblems to be solved to completion.
The first major iteration is special: it terminates as soon as the
linear constraints and bounds are satisfied (if possible), ignoring
the nonlinear constraints.
In general it is unsafe to specify a value as small as
k = 1 or 2.
(Even when an optimal solution has been reached, a few minor
iterations may be needed for the corresponding subproblem to be
recognized as optimal.)
|
|
|
|
|
Optimality tolerance |
t |
Default = 1.0e-6 |
|
|
|
|
|
Penalty parameter |
r |
Default = 1.0 |
This specifies that the initial value of ρ
k in the augmented
Lagrangian (5) should be
r times a certain default value
100/
m1, where
m1 is the number of nonlinear constraints. It is
used when
Lagrangian = Yes (the default setting).
For early runs on a problem with unknown characteristics, the
default value should be acceptable. If the problem is highly
nonlinear and the major iterations do not converge, a larger value
such as 2 or 5 may help. In general, a positive
r may be necessary
to ensure convergence,
even for convex programs.
On the other hand, if
r is too large, the rate of convergence may
be unnecessarily slow. If the functions are not highly nonlinear or
a good starting point is known, it is often safe to specify
Penalty parameter 0.0.
If several related problems are to be solved, the following strategy
for setting the
Penalty parameter may be useful:
-
Initially, use a moderate value for r (such as the default) and
a reasonably low Iterations and/or Major iterations limit.
- If successive major iterations appear to be terminate with radically
different solutions, try increasing the penalty parameter.
(See also the Major damping parameter.)
- If there appears to be little progress between major iterations,
it may help to reduce the penalty parameter.
|
|
|
|
|
Radius of convergence |
r |
Default = 0.01 |
This determines when the penalty parameter ρ
k is reduced (if
initialized to a positive value). Both the nonlinear constraint
violation (see
rowerr below) and the relative change in
consecutive Lagrange multiplier estimates must be less than
r at
the start of a major iteration before ρ
k is reduced or set to
zero.
A few major iterations later, full completion is requested if not
already set, and the remaining sequence of major iterations should
converge quadratically to an optimum.
|
|
|
|
|
Row tolerance |
t |
Default = 1.0e-6 |
This specifies how accurately the nonlinear constraints should be
satisfied at a solution. The default value is usually small enough,
since model data is often specified to about that accuracy.
Let
viol be the maximum violation of the nonlinear constraints
(2), and let
rowerr =
viol / (1 +
xnorm), where
xnorm is a
measure of the size of the current solution (
x,
y). The solution is
regarded as acceptably feasible if
rowerr ≤
t.
If the problem functions involve data that is known to be of low
accuracy, a larger
Row tolerance may be appropriate. On the
other hand, nonlinear constraints are often satisfied with rapidly
increasing accuracy during the last few major iterations. It is
common for the final solution to satisfy
rowerr =
O(є).
|
|
|
|
|
Scale option |
l |
Default = 2 (LP) or 1 (NLP) |
|
Scale |
Yes |
|
Scale |
No |
|
Scale linear variables |
|
Same as Scale option 1 |
|
Scale nonlinear variables |
|
Same as Scale option 2 |
|
Scale all variables |
|
Same as Scale option 2 |
|
Scale tolerance |
r |
Default = 0.9 |
|
Scale, Print |
|
Scale, Print, Tolerance |
r |
Three scale options are available as follows:
-
l = 0
- No scaling. If storage is at a premium, this option
saves m+n words of workspace.
- l = 1
- Linear constraints and variables are scaled by an
iterative procedure that attempts to make the
matrix coefficients as close as possible to 1.0.
- l = 2
- All constraints and variables are scaled by the iterative
procedure. Also, a certain additional scaling is performed
that may be helpful if the right-hand side b or the
solution x is large. This takes into
account columns of ( A I ) that are fixed or have positive
lower bounds or negative upper bounds.
Scale option 1 is the default for nonlinear problems. (Only
linear variables are scaled.)
Scale Yes sets the default scaling.
Caution: If all
variables are nonlinear,
Scale Yes unexpectedly does nothing,
because there are no linear variables to scale.)
Scale No
suppresses scaling (equivalent to
Scale option 0).
With nonlinear constraints,
Scale option 1 or
0 should
generally be tried first.
Scale option 2 gives scales that
depend on the initial Jacobian, and should therefore be used only if
(a) a good starting point is provided, and (b) the problem is not
highly nonlinear.
|
|
|
|
|
Verify level |
l |
Default = 0 |
|
Verify objective gradients |
|
Same as Verify level 1 |
|
Verify constraint gradients |
|
Same as Verify level 2 |
|
Verify |
|
Same as Verify level 3 |
|
Verify gradients |
|
Same as Verify level 3 |
|
Verify |
Yes |
Same as Verify level 3 |
|
Verify |
No |
Same as Verify level 0 |
This option refers to a finite-difference check on the gradients
(first derivatives) of each nonlinear function. It occurs before a
problem is scaled, and before the first basis is factorized.
(Hence, the variables may not yet satisfy the general linear
constraints.)
-
l = 0
- Only a “cheap" test is performed, requiring
three evaluations of the nonlinear objective (if any) and two
evaluations of the nonlinear constraints.
- l = 1
- A more reliable check is made on each component
of the objective gradient.
- l = 2
- A check is made on each column of the Jacobian matrix
associated with the nonlinear constraints.
- l = 3
- A detailed check is made on both the objective and
the Jacobian.
- l = −1
- No checking is performed. This may be necessary
if the functions are undefined at the starting point.
6.2.6 Options for Input and Output
The following options specify various files to be used, and the
amount of printed output required.
|
|
|
|
|
Print level |
l |
Default = 0 |
|
Print frequency |
k |
Default = 100 |
The PRINT file provides more complete information than the
SUMMARY file. It includes a listing of the main options,
statistics about the problem, scaling information, the iteration
log, the exit condition, and (optionally) the final solution. It
also includes error messages.
The files are specified in
Prob.SOL.PrintFile and
Prob.SOL.SummFile.
For problems with linear constraints,
Print level 0 gives most of the normal output.
Print level 1 produces statistics for
the basis matrix
B and its
LU factors
each time the basis is factorized.
Print frequency k produces one line of the iteration
log every
k minor iterations.
Print frequency 1
causes every minor iteration to be logged.
Print frequency 0 is shorthand for
k = 99999.
For problems with nonlinear constraints,
Print level 0 produces just one line of output
per major iteration.
This provides a short summary of the progress of the
optimization. The
Print frequency is ignored.
If
Print level > 0, certain quantities are printed at the
start of each major iteration, and minor iterations are logged
according to the
Print frequency.
In the latter case, the value of
l is best thought of as a binary
number of the form
Print level JFLXB
where each letter stands for a digit that is either 0 or 1. The
quantities referred to are:
-
B Basis statistics, as mentioned above.
- X xk, the nonlinear variables involved
in the objective function or the constraints.
- L λk, the Lagrange-multiplier estimates
for the nonlinear constraints. (Suppressed if
Lagrangian = No, since then λk = 0.)
- F f(xk), the values of the nonlinear
constraint functions.
- J J(xk), the Jacobian matrix.
To obtain output of any item, set the corresponding digit to 1,
otherwise to 0. For example,
Print level 10 sets
X = 1
and the other digits equal to zero. The nonlinear variables will be
printed each major iteration.
If
J = 1, the Jacobian is output column-wise. Column
j is
preceded by the value of the corresponding variable
xj and a key
to indicate whether the variable is basic, superbasic or nonbasic.
(Hence if
J = 1, there is no reason to specify
X = 1
unless the objective contains more nonlinear variables than the
Jacobian.) A typical line of output is
3 1.250000D+01 BS 1 1.00000D+00 4 2.00000D+00
which means that
x3 is basic at value 12.5, and the third column
of the Jacobian has elements of 1.0 and 2.0 in rows 1 and 4.
|
|
|
|
|
Solution |
Yes |
Default |
|
Solution |
No |
The
Yes and
No options control whether the final solution is
output to the PRINT file. Numerical values are printed in
f16.5 format where possible.
The special values 0, 1 and −1 are printed as
.,
1.0 and
-1.0. Bounds outside the range (−10
20,10
20) appear as
the word
None.
|
|
|
|
|
Summary file |
f |
Default = 6 (typically) |
|
Summary level |
l |
Default = 0 |
|
Summary frequency |
k |
Default = 100 |
The SUMMARY file provides a brief form of the iteration log and
the exit condition. It also includes error messages. In an
interactive environment, the output normally appears at the screen
and allows a run to be monitored.
For problems with linear constraints,
Summary level 0 produces brief output.
Summary level 1 gives a few additional messages.
Summary frequency k produces one line of the iteration
log every
k minor iterations.
Summary frequency 1
causes every minor iteration to be logged.
Summary frequency 0 is shorthand for
k = 99999.
For problems with nonlinear constraints,
Summary level 0
produces one line of output per major iteration.
This provides a short summary of the progress of the
optimization. The
Summary frequency is ignored.
If
Summary level > 0, certain quantities are printed at the
start of each major iteration, and minor iterations are logged
according to the
Summary frequency.
6.3 File Output
6.3.1 The PRINT file
The following information is output to the PRINT file during the
solution process. The longest line of output is 124 characters.
| • |
A listing of the SPECS file, if any. |
| • |
The selected options. |
| • |
An estimate of the storage needed and the amount available. |
| • |
Some statistics about the problem data. |
| • |
The storage available for the LU factors of the basis matrix. |
| • |
A log from the scaling procedure, if Scale option > 0. |
| • |
Notes about the initial basis obtained from CRASH or a BASIS file. |
| • |
The major iteration log. |
| • |
The minor iteration log. |
| • |
Basis factorization statistics. |
| • |
The EXIT condition and some statistics about the solution obtained. |
| • |
The printed solution, if requested. |
The last five items are described in the following sections.
6.3.2 The major iteration log
Problems with nonlinear constraints require several
major
iterations to reach a solution, each involving the solution of an
LC subproblem (a linearly constrained subproblem that
generates search directions for
x and λ). If
Print
level = 0, one line of information is output to the PRINT file
each major iteration. An example log is shown in
Figure
1.
Major minor total ninf step objective Feasible Optimal nsb ncon LU penalty BSwap
1 1T 1 0 0.0E+00 0.00000000E+00 0.0E+00 1.2E+01 8 4 31 1.0E-01 0
2 13 14 0 1.0E+00 2.67011596E+00 4.4E-06 2.8E-03 7 23 56 1.0E-01 8
Completion Full now requested
3 3 17 0 1.0E+00 2.67009870E+00 3.1E-08 1.4E-06 7 29 41 1.0E-01 0
4 0 17 0 1.0E+00 2.67009863E+00 5.6E-17 1.4E-06 7 30 41 1.0E-02 0
Figure 1: The Major Iteration log
-
Label
-
Description
- Major
-
The current major iteration number.
- minor
-
is the number of iterations required by both the feasibility
and optimality phases of the QP subproblem. Generally,
Mnr will be 1 in the later iterations, since theoretical
analysis predicts that the correct active set will be
identified near the solution.
- total
-
The total number of minor iterations.
- ninf
-
The number of infeasibilities in the LC subproblem. Normally 0,
because the bounds on the linearized constraints are relaxed
in several stages until the constraints are “feasible”.
- step
-
The step length α taken along the current search
direction p. The variables x have just been changed to x
+ α p. On reasonably well-behaved problems,
step=1.0
as the solution is approached, meaning the new estimate of
(x,λ) is the solution of the LC subproblem.
- objective
-
The value of true objective function.
- Feasible
-
The value of rowerr, the maximum component of the
scaled nonlinear constraint residual. The
solution is regarded as acceptably feasible if Feasbl is
less than the Row tolerance.
- Optimal
-
The value of maxgap, the maximum complementarity
gap. It is an estimate of the
degree of nonoptimality of the reduced costs.
Both Feasible and Optimal are small in the neighborhood
of a solution.
- nsb
-
The current number of superbasic variables.
- ncon
-
The number of times subroutine funcon has been called to
evaluate the nonlinear constraint functions.
The Jacobian has been evaluated or approximated essentially
the same number of times. (Function evaluations needed
to estimate the Jacobian by finite differences are
not included.)
- LU
-
The number of nonzeros in the sparse LU factors of the basis
matrix on completion of the LC subproblem. (The factors are
computed at the start of each major iteration, and updated
during minor iterations whenever a basis change occurs.)
-
-
As the solution is approached and the minor iterations
decrease towards zero, LU reflects the
number of nonzeros in the LU factors at the start of the
LC subproblem.
- penalty
-
The penalty parameter ρk used in the modified
augmented Lagrangian that defines the objective function
for the LC subproblem.
- BSwap
-
The number of columns of the basis matrix B that were
swapped with columns of S to improve the condition of B.
The swaps are determined by an LU factorization of the
rectangular matrix BS = ( B S )T with stability
being favored more than sparsity.
Itn ph pp rg +sbs -sbs -bs step pivot ninf sinf,objective L U ncp nobj ncon nsb Hmod cond(H) conv
1 1 1 -1.0E+00 2 2 1 3.0E+01 1.0E+00 1 1.35000000E+02 0 19 0
2 1 1 -1.0E+00 27 27 102 7.0E+01 1.0E+00 1 1.05000000E+02 0 19 0
3 1 1 -1.0E+00 3 3 27 3.0E+01 -1.0E+00 1 3.50000000E+01 1 19 0
4 1 1 -1.0E+00 28 28 26 4.9E-11 1.0E+00 1 5.00000000E+00 1 20 0
5 1 1 -1.0E+00 47 47 2 4.9E-11 1.0E+00 1 5.00000000E+00 1 20 0
6 1 1 1.0E+00 27 27 101 5.0E+00 -1.0E+00 1 5.00000000E+00 2 20 0
Itn 6 -- feasible solution. Objective = -1.818044887E+02
7 3 1 -1.7E+01 87 0 0 1.0E+00 0.0E+00 0 -2.77020571E+02 4 21 0 6 0 1 1 0 1.0E+00 FFTT
8 3 1 -1.7E+01 72 0 0 1.9E-01 0.0E+00 0 -3.05336895E+02 4 21 0 8 0 2 1 0 5.5E+00 FFTT
9 3 1 -2.3E+01 41 0 0 1.0E+00 0.0E+00 0 -4.43743832E+02 4 21 0 9 0 3 1 0 6.5E+00 FFFF
10 4 1 6.6E-01 0 0 0 6.0E+00 0.0E+00 0 -5.64075338E+02 4 21 0 11 0 3 1 0 3.5E+00 FFTT
...
Itn ph pp rg +sbs -sbs -bs step pivot ninf sinf,objective L U ncp nobj ncon nsb Hmod cond(H) conv
161 4 1 8.8E-03 0 73 71 4.2E+00 1.0E+00 0 -1.73532497E+03 4 20 0 340 0 17 1 1 9.6E+00 TTTF
162 3 1 -3.5E-02 6 0 0 1.5E+00 0.0E+00 0 -1.73533264E+03 4 20 0 342 0 18 1 0 1.3E+02 TTFF
163 4 1 2.9E-02 0 0 0 4.5E+00 0.0E+00 0 -1.73533617E+03 4 20 0 344 0 18 1 0 2.0E+01 TTFF
164 4 1 2.1E-02 0 0 0 2.3E+01 0.0E+00 0 -1.73538331E+03 4 20 0 347 0 18 1 0 9.8E+00 TTFF
165 4 1 3.0E-02 0 0 0 5.0E+00 0.0E+00 0 -1.73552261E+03 4 20 0 349 0 18 1 0 2.1E+01 TTFF
166 4 1 1.2E-02 0 0 0 1.0E+00 0.0E+00 0 -1.73556089E+03 4 20 0 350 0 18 1 0 2.2E+01 TTTF
tolrg reduced to 1.162E-03 lvltol = 1
167 4 1 2.3E-03 0 0 0 1.0E+00 0.0E+00 0 -1.73556922E+03 4 20 0 351 0 18 1 0 2.2E+01 TTFF
168 4 1 1.2E-03 0 0 0 7.9E-01 0.0E+00 0 -1.73556953E+03 4 20 0 353 0 18 1 0 2.1E+01 TTFF
169 4 1 1.0E-04 0 0 0 1.0E+00 0.0E+00 0 -1.73556958E+03 4 20 0 354 0 18 1 0 2.0E+01 TTTT
tolrg reduced to 1.013E-05 lvltol = 1
170 4 1 2.9E-05 0 0 0 1.1E+00 0.0E+00 0 -1.73556958E+03 4 20 0 356 0 18 1 0 1.7E+01 TTFF
171 4 1 1.0E-05 0 0 0 1.0E+00 0.0E+00 0 -1.73556958E+03 4 20 0 357 0 18 1 0 1.7E+01 TTFF
172 4 1 1.5E-06 0 0 0 1.2E+00 0.0E+00 0 -1.73556958E+03 4 20 0 359 0 18 1 0 1.7E+01 TTTF
tolrg reduced to 1.000E-06 lvltol = 2
173 4 1 2.4E-07 0 0 0 1.0E+00 0.0E+00 0 -1.73556958E+03 4 20 0 360 0 18 1 0 1.7E+01 TTTF
Biggest dj = 3.583E-03 (variable 25) norm rg = 2.402E-07 norm pi = 1.000E+00
Figure 2: The Minor Iteration log
6.3.3 The minor iteration log
If
Print level ≥ 1, one line of information is output to
the PRINT file every
kth minor iteration, where
k is the
specified
Print frequency (default
k=
100). A heading is
printed periodically. Problem
t5weapon gives the log shown in
Figure
2.
-
Label
-
Description
- Itn
-
The current minor iteration number.
- ph
-
The current phase of the solution procedure:
-
1 Phase 1 simplex method, trying to satisfy the
linear constraints. The current solution is
an infeasible vertex.
- 2 Phase 2 simplex method, solving a linear program.
- 3 Reduced-gradient method. A nonbasic variable
has just become superbasic.
- 4 Reduced-gradient method, optimizing the current
set of superbasic variables.
- pp
-
The Partial Price indicator.
The variable selected by the
last PRICE operation came from the ppth partition of A
and I. pp is set to zero when the basis is refactored.
-
A PRICE operation is defined to be the process by which a nonbasic
variable is selected to become a new superbasic. The selected
variable is denoted by jq. Variable jq often becomes basic
immediately. Otherwise it remains superbasic, unless it reaches its
opposite bound and becomes nonbasic again. If Partial price is
in effect, variable jq is selected from App or
Ipp, the ppth segments of the constraint matrix
( A I ).
- rg
-
In Phase 1, 2 or 3, this is dj, the reduced cost (reduced gradient) of the
variable jq selected by PRICE at the start of the present
iteration. Algebraically, dj=gj − πT aj for
j=jq, where gj is the gradient of the current
objective function, π is the vector of dual variables for
the problem (or LC subproblem), and aj is the jth column of
the current ( A I ).
-
In Phase 4, rg is the largest reduced gradient
among the superbasic variables.
- +sbs
-
The variable jq selected by PRICE to be added to the
superbasic set.
- -sbs
-
The variable chosen to leave the set of superbasics. It has become
basic if the entry under -bs is nonzero; otherwise it has become
nonbasic.
- -bs
-
The variable removed from the basis (if any) to become nonbasic.
- step
-
The step length α taken along the current search
direction p. The variables x have just been changed to
x + α p.
- pivot
-
If column aq replaces the rth column of the basis B,
pivot is the rth element of a vector y satisfying
By = aq. Wherever possible, step is chosen to avoid
extremely small values of pivot (because they cause the
basis to be nearly singular). In rare cases, it may be
necessary to increase the Pivot tolerance to exclude very
small elements of y from consideration during the computation
of step.
- ninf
-
The number of infeasibilities before the present
iteration. This number decreases monotonically.
- sinf,objective
-
If ninf>0, this is sinf, the sum of infeasibilities
before the present iteration. It usually decreases at
each nonzero step, but if ninf decreases by 2 or more,
sinf may occasionally increase.
Otherwise it is the value of the current objective function
after the present iteration.
For linear programs, it means the true linear objective function.
For problems with linear constraints, it means the sum of the
linear objective and the value returned by subroutine funobj.
For problems with nonlinear constraints, it is the quantity
just described if Lagrangian = No; otherwise it is the value
of the augmented Lagrangian for the current major iterations
(which tends to the true objective as convergence is approached).
- L
-
The number of nonzeros representing the basis factor L.
Immediately after a basis factorization B = LU, this is
lenL, the number of subdiagonal elements in the columns of a
lower triangular matrix. Further nonzeros are added to L
when various columns of B are later replaced. (Thus, L
increases monotonically.)
- U
-
The number of nonzeros in the basis factor U. Immediately
after a basis factorization, this is lenU, the number of
diagonal and superdiagonal elements in the rows of an
upper-triangular matrix. As columns of B are replaced, the
matrix U is maintained explicitly (in sparse form). The value
of U may fluctuate up or down; in general it will tend to
increase.
- ncp
-
The number of compressions required to recover storage in the
data structure for U. This includes the number of
compressions needed during the previous basis factorization.
Normally ncp should increase very slowly. If not, the
amount of workspace available to MINOS should
be increased by a significant amount. As a suggestion, the work
array z(*) should be extended by 2(L+U) elements.
The following items are printed if the problem is
nonlinear or if the superbasic set is non-empty (i.e., if the
current solution is not a vertex).
-
Label
- Description
- nobj
-
The number of times subroutine funobj has been called.
- ncon
-
The number of times subroutine funcon has been called.
- nsb
-
The current number of superbasic variables.
- Hmod
-
An indication of the type of modifications made to
the triangular matrix R that is used to approximate the reduced Hessian
matrix. Two integers i1 and i2 are shown. They will remain zero
for linear problems. If i1=1, a
BFGS quasi-Newton update has been made to R, to account for a move within
the current subspace. (This will not occur if the solution is infeasible.)
If i2=1, R has been modified to account for a change in basis.
This will sometimes occur even if the solution is infeasible (if
a feasible point was obtained at some earlier stage).
-
Both updates are implemented by triangularizing the matrix
R + vwT for some vectors v and w.
If an update fails for numerical reasons, i1 or i2 will be set to 2,
and the resulting R will be nearly singular. (However, this is highly
unlikely.)
- cond(H)
-
An estimate of the condition number of the reduced Hessian.
It is the square of the ratio of the largest and smallest
diagonals of the upper triangular matrix R—a lower
bound on the condition number of the matrix RTR that approximates the
reduced Hessian. cond(H) gives a rough indication of whether
or not the optimization procedure is having difficulty.
The reduced-gradient
algorithm will make slow progress if cond(H) becomes as large as
108, and will probably fail to find a better solution if
cond(H) reaches 1012 or more.
-
To guard against high values of cond(H), attention should be
given to the scaling of the variables and the constraints. In some
cases it may be necessary to add upper or lower bounds to certain
variables to keep them a reasonable distance from singularities in
the nonlinear functions or their derivatives.
- conv
-
A set of four logical variables C1, C2, C3, C4
that are used to determine when to discontinue optimization in the
current subspace (Phase 4) and consider releasing a nonbasic
variable from its bound (the PRICE operation of Phase 3). Let
rg be the norm of the reduced gradient, as described above.
The meaning of the variables Cj is as follows:
| C1 is true if the change in x was sufficiently small; |
| C2 is true if the change in the objective was sufficiently small; |
| C3 is true if rg is smaller than some loose tolerance
TOLRG; |
| C4 is true if rg is smaller than some tighter tolerance. |
if (C1 and C2 and C3) or C4 then go to Phase 3.
At present, tolrg = t |dj|, where t is
the Subspace tolerance (nominally 0.5) and dj is the
reduced-gradient norm at the most recent Phase 3 iteration. The
“tighter tolerance" is the maximum of 0.1 tolrg and
10−7 π
π . Only the tolerance t can be altered at
run-time.
. Only the tolerance t can be altered at
run-time.
6.3.4 Crash statistics
The following items are output to the PRINT file when no warm
start is used. They refer to the number of columns that the CRASH
procedure selects during several passes through
A while searching
for a triangular basis matrix.
-
Label
- Description
- Slacks
-
is the number of slacks selected initially.
- Free cols
-
is the number of free columns in the basis,
including those whose bounds are rather far apart.
- Preferred
-
is the number of “preferred” columns in the basis (i.e.,
hs(j) = 3 for some j ≤ n). It will be a
subset of the columns for which hs(j) = 3 was
specified.
- Unit
-
is the number of unit columns in the basis.
- Double
-
is the number of columns in the basis containing 2 nonzeros.
- Triangle
-
is the number of triangular columns in the basis
with 3 or more nonzeros.
- Pad
-
is the number of slacks used to pad the basis
(to make it a nonsingular triangle).
6.3.5 Basis factorization statistics
If
Print level ≥ 1, the following items are output to the
PRINT file whenever the basis
B or the rectangular matrix
BS =
(
B S )
T is factorized. Note that
BS may be factorized at
the start of just some of the major iterations. It is immediately
followed by a factorization of
B itself.
Gaussian elimination is used to compute a sparse LU factorization of
B or
BS, where
PLPT and
PUQ are lower and upper triangular
matrices for some permutation matrices
P and
Q.
-
Label
- Description
- Factorize
- The number of factorizations since the start of the run.
- Demand
- A code giving the reason for the present factorization.
- Itn
- The current iteration number.
- Nonlin
- The number of nonlinear variables in the current basis B.
- Linear
- The number of linear variables in B.
- Slacks
- The number of slack variables in B.
- m
- The number of rows in the matrix being factorized (B or B S).
- n
- The number of columns in the matrix being factorized. Preceded by “=” if the matrix is B; by “>” if it is B S.
- Elems
- The number of nonzero elements in B or B S.
- Amax
- The largest nonzero in B or B S.
- Density
- The density of the matrix (percentage of nonzeros).
- Merit
- The average Markowitz merit count for the elements chosen to be the diagonals of PUQ. Each merit count is defined to be (c−1)(r−1) where c and r are the number of nonzeros in the column and row containing the element at the time it is selected to be the next diagonal. Merit is the average of m such quantities. It gives an indication of how much work was required to preserve sparsity during the factorization.
- lenL
- The number of nonzeros in the factor L.
- L+U
- The number of nonzeros in both L and U.
- Cmprssns
- The number of times the data structure holding the partially factored matrix needed to be compressed to recover unused storage. Ideally this number should be zero. If it is more than 3 or 4, the amount of workspace available to MINOS should be increased for efficiency.
- Incres
- The percentage increase in the number of nonzeros in L and U relative to the number of nonzeros in B or B S.
- Utri
- The size of the “backward triangle” in B or B S. These top rows of U come directly from the matrix.
- lenU
- The number of nonzeros in the factor U.
- Ltol
- The maximum allowed size of nonzeros in L. Usually equal to the LU factor tolerance.
- Umax
- The maximum nonzero in U.
- Ugrwth
- The ratio Umax / Amax.
- Ltri
- The size of the “forward triangle” in B or B S. These initial columns of L come directly from the matrix.
- dense1
- is the number of columns remaining when the density of the basis matrix being factorized reached 0.3.
- Lmax
- The maximum nonzero in L (no larger than Ltol).
- Akmax
- The maximum nonzero arising during the factorization. (Printed only if Theshold Complete Pivoting is in effect.)
- Agrwth
- The ratio Akmax / Amax. (Printed only if Theshold Complete Pivoting is in effect.)
- bump
- The number of columns of B or B S excluding Utri and Ltri.
- dense2
- The number of columns remaining when the density of the basis matrix being factorized reached 0.6.
- DUmax
- The largest diagonal of U (really PUQ).
- DUmin
- The smallest diagonal of U.
- condU
- The ratio DUmax / DUmin. As long as Ltol is not large (say 10.0 or less), condU is an estimate of the condition number of B. If this number is extremely large, the basis is nearly singular and some numerical difficulties might occur. (However, an effort is made to avoid near-singularity by using slacks to replace columns of B that would have made Umin extremely small. Messages are issued to this effect, and the modified basis is refactored.)
6.3.6 EXIT conditions
When the solution procedure terminates, an
EXIT – message is
printed to summarize the final result. Here we describe each
message and suggest possible courses of action.
The number associated with each EXIT is the output value of the
integer variable
inform.
| The following messages arise when the SPECS file is found
to
contain no further problems. |
MINOS encountered end-of-file or an endrun card before finding a SPECS file.
Otherwise, the SPECS file may be empty, or cards containing the
keywords
Skip or
Endrun may imply that all problems should
be ignored.
-1 ENDRUN
This message is printed at the end of a run if
MINOS terminates of its own accord. Otherwise, the operating
system will have intervened for one of many possible reasons (excess
time, missing file, arithmetic error in user routines, etc.).
| The following messages arise when a solution exists (though
it
may not be optimal). |
This is the message we all
hope to see! It is certainly preferable to every other message, and
we naturally want to believe what it says, because this is surely
one situation where
the computer knows best. There may be
cause for celebration if the objective function has reached an
astonishing new high (or low).
In all cases, a distinct level of caution is in order, even if it
can wait until next morning. For example, if the objective value
is much better than expected, we may have obtained an optimal
solution to the wrong problem! Almost any item of data could have
that effect if it has the wrong value. Verifying that the problem
has been defined correctly is one of the more difficult tasks for a
model builder. It is good practice in the function subroutines to
print any data that is input during the first entry.
If nonlinearities exist, one must always ask the question: could there
be more than one local optimum? When the constraints are linear and
the objective is known to be convex (e.g., a sum of squares) then
all will be well if we are
minimizing the objective: a local
minimum is a global minimum in the sense that no other point has a
lower function value. (However, many points could have the
same objective value, particularly if the objective is
largely linear.) Conversely, if we are
maximizing a convex
function, a local maximum cannot be expected to be global, unless
there are sufficient constraints to confine the feasible region.
Similar statements could be made about nonlinear constraints defining
convex or concave regions. However, the functions of a problem are
more likely to be neither convex nor concave. Always specify a good
starting point if possible, especially for nonlinear variables, and
include reasonable upper and lower bounds on the variables to
confine the solution to the specific region of interest. We expect
modelers to
know something about their problem, and to make
use of that knowledge as well as they can.
One other caution about “
Optimal solution”s.
Some of the variables or slacks may lie outside their bounds more
than desired, especially if scaling was requested.
Max Primal
infeas refers to the largest bound infeasibility and which variable
(or slack) is involved. If it is too large, consider restarting
with a smaller
Feasibility tolerance (say 10 times smaller)
and perhaps
Scale option 0.
Similarly,
Max Dual infeas indicates which variable is most
likely to be at a non-optimal value. Broadly speaking, if
Max Dual infeas/Norm of pi = 10−d,
then the objective function would probably change in the
dth
significant digit if optimization could be continued. If
d seems
too large, consider restarting with smaller
Optimality
tolerances.
Finally,
Nonlinear constraint violn shows the maximum
infeasibility for nonlinear rows. If it seems too large, consider
restarting with a smaller
Row tolerance.
1 EXIT – the problem is infeasible
When the constraints are
linear, this message can probably be trusted. Feasibility is
measured with respect to the upper and lower bounds on the variables
and slacks. Among all the points satisfying the general constraints
Ax +
s = 0, there is apparently no point that satisfies the bounds
on
x and
s. Violations as small as the
Feasibility
tolerance are ignored, but at least one component of
x or
s
violates a bound by more than the tolerance.
When nonlinear constraints are present, infeasibility is
much
harder to recognize correctly. Even if a feasible solution exists,
the current linearization of the constraints may not contain a
feasible point. In an attempt to deal with this situation, when
solving each linearly constrained (LC) subproblem, MINOS is
prepared to relax the bounds on the slacks associated with nonlinear
rows.
If an LC subproblem proves to be infeasible or unbounded (or if the
Lagrange multiplier estimates for the nonlinear constraints become
large), MINOS enters so-called “nonlinear elastic” mode. The
subproblem includes the original QP objective and the sum of the
infeasibilities—suitably weighted using the
Elastic weight
parameter. In elastic mode, some of the bounds on the nonlinear rows
“elastic”—i.e., they are allowed to violate their specified
bounds. Variables subject to elastic bounds are known as
elastic variables. An elastic variable is free to violate one
or both of its original upper or lower bounds. If the original
problem has a feasible solution and the elastic weight is
sufficiently large, a feasible point eventually will be obtained for
the perturbed constraints, and optimization can continue on the
subproblem. If the nonlinear problem has no feasible solution,
MINOS will tend to determine a “good” infeasible point if the
elastic weight is sufficiently large. (If the elastic weight were
infinite, MINOS would locally minimize the nonlinear constraint
violations subject to the linear constraints and bounds.)
Unfortunately, even though MINOS locally minimizes the nonlinear
constraint violations, there may still exist other regions in which
the nonlinear constraints are satisfied. Wherever possible,
nonlinear constraints should be defined in such a way that feasible
points are known to exist when the constraints are linearized.
2 EXIT – the problem is unbounded (or badly scaled)
EXIT – violation limit exceeded – the problem may be unbounded
For linear problems, unboundedness is detected by the
simplex method when a nonbasic variable can apparently be increased
or decreased by an arbitrary amount without causing a basic variable
to violate a bound. A message prior to the EXIT message will give
the index of the nonbasic variable. Consider adding an upper or
lower bound to the variable. Also, examine the constraints that have
nonzeros in the associated column, to see if they have been
formulated as intended.
Very rarely, the scaling of the problem could be so poor that numerical
error will give an erroneous indication of unboundedness. Consider
using the
Scale option.
For nonlinear problems, MINOS monitors both the size of the
current objective function and the size of the change in the
variables at each step. If either of these is very large (as judged
by the
Unbounded parameters, the problem is terminated and
declared UNBOUNDED. To avoid large function values, it may be
necessary to impose bounds on some of the variables in order to keep
them away from singularities in the nonlinear functions.
The second message indicates an abnormal termination while enforcing
the limit on the constraint violations. This exit implies that the
objective is not bounded below in the feasible region defined by
expanding the bounds by the value of the
Violation limit.
3 EXIT – major iteration limit exceeded
EXIT – minor iteration limit exceeded
EXIT – too many iterations
Either the
Iterations limit or the
Major
iterations limit was exceeded before the required solution could be
found. Check the iteration log to be sure that progress was being
made. If so, restart the run using a basis file that was saved (or
should have been saved!) at the end of the run.
4 EXIT – requested accuracy could not be achieved
A feasible solution has been found, but the requested accuracy in the
dual infeasibilities could not be achieved. An abnormal termination
has occurred, but MINOS is within 10
−2 of satisfying the
Major optimality tolerance. Check that the
Major optimality
tolerance is not too small.
5 EXIT – the superbasics limit is too small: nnn
The
problem appears to be more nonlinear than anticipated. The current
set of basic and superbasic variables have been optimized as much as
possible and a PRICE operation is necessary to continue, but there
are already
nnn superbasics (and no room for any more).
In general, raise the
Superbasics limit s by a reasonable
amount, bearing in mind the storage needed for the reduced Hessian
(about 1/2
s2 double words).
6 EXIT – constraint and objective values could not be calculated
This exit occurs if a value
mode ≤ −1 is set
during some call to
funobj or
funcon. MINOS assumes that
you want the problem to be abandoned forthwith.
In some environments, this exit means that your subroutines were not
successfully linked to MINOS. If the default versions of
funobj and
funcon are ever called, they issue a warning
message and then set
mode to terminate the run.
7 EXIT – subroutine funobj seems to be giving incorrect gradients
A check has been made on some individual elements of the
objective gradient array at the first point that satisfies the
linear constraints. At least one component
gObj(j) is being
set to a value that disagrees markedly with a forward-difference
estimate of ∂
f /
∂
xj. (The relative difference between the computed and estimated
values is 1.0 or more.) This exit is a safeguard, since MINOS
will usually fail to make progress when the computed gradients are
seriously inaccurate. In the process it may expend considerable
effort before terminating with EXIT 9 below.
Check the function and gradient computation
very carefully in
funobj. A simple omission (such as forgetting to divide
fObj by 2) could explain everything. If
fObj or
gObj(j) is very large, then give serious thought to scaling
the function or the nonlinear variables.
If you feel
certain that the computed
gObj(j) is correct
(and that the forward-difference estimate is therefore wrong), you
can specify
Verify level 0 to prevent individual elements from
being checked. However, the optimization procedure may have
difficulty.
8 EXIT – subroutine funcon seems to be giving incorrect gradients
This is analogous to the preceding exit. At least one of
the computed Jacobian elements is significantly different from an
estimate obtained by forward-differencing the constraint vector
F(
x). Follow the advice given above, trying to ensure that the
arrays
fCon and
gCon are being set correctly in
funcon.
9 EXIT – the current point cannot be improved upon
Several
circumstances could lead to this exit.
-
Subroutines funobj or funcon could be
returning accurate function values but inaccurate gradients (or
vice versa). This is the most likely cause. Study the
comments given for EXIT 7 and 8, and do your best to ensure
that the coding is correct.
- The function and gradient values could be consistent, but their
precision could be too low. For example, accidental use of a
real data type when double precision was intended
would lead to a relative function precision of about
10−6 instead of something like 10−15. The default
Optimality tolerance of 10−6 would need to be raised to
about 10−3 for optimality to be declared (at a rather
suboptimal point). Of course, it is better to revise the function
coding to obtain as much precision as economically possible.
- If function values are obtained from an expensive iterative
process, they may be accurate to rather few significant figures,
and gradients will probably not be available. One should specify
| Function precision |
|
t |
| Major optimality tolerance |
|
√t |
10 EXIT – cannot satisfy the general constraints
An LU
factorization of the basis has just been obtained and used to
recompute the basic variables
x B, given the present values of the
superbasic and nonbasic variables. A step of “iterative
refinement” has also been applied to increase the accuracy of
x B. However, a row check has revealed that the resulting solution
does not satisfy the current constraints
Ax −
s = 0 sufficiently
well.
This probably means that the current basis is very ill-conditioned.
Try
Scale option 1 if scaling has not yet been used and there
are some linear constraints and variables.
For certain highly structured basis matrices (notably those with band
structure), a systematic growth may occur in the factor
U. Consult
the description of
Umax,
Umin and
Growth in
§
6.3.5, and set the
LU factor tolerance to
2.0 (or possibly even smaller, but not less than 1.0).
12 EXIT – terminated from subroutine s1User
The user has
set the value
iAbort = 1 in subroutine
s1User. MINOS
assumes that you want the problem to be abandoned forthwith.
| If the following exits occur during the first basis
factorization, the primal and dual variables x and pi
will have their original input values.
BASIS files will be saved if requested, but certain values
in the printed solution will not be meaningful. |
The main integer or real storage array
iw(*) or
rw(*) is apparently not large enough for this problem. The
routine declaring
iw and
rw should be recompiled with a
larger dimensions for those arrays. The new values should also be
assigned to
leniw and
lenrw.
An estimate of the additional storage required is given in messages
preceding the exit.
21 EXIT – error in basis package
A preceding message will
describe the error in more detail. One such message says that the
current basis has more than one element in row
i and column
j.
This could be caused by a corresponding error in the input
parameters
a(*),
ha(*), and
ka(*).
22 EXIT – singular basis after nnn factorization attempts
This exit is highly unlikely to occur. The first factorization
attempt will have found the basis to be structurally or numerically
singular. (Some diagonals of the triangular matrix
U were
respectively zero or smaller than a certain tolerance.) The
associated variables are replaced by slacks and the modified basis
is refactorized, but singularity persists. This must mean that the
problem is badly scaled, or the
LU factor tolerance is too much
larger than 1.0.
| If the following messages arise, either an OLD BASIS file
could not be loaded properly, or some fatal system error has
occurred. New BASIS files cannot be saved, and there is no
solution to print. The problem is abandoned. |
On the first line of the OLD BASIS file, the dimensions
labeled
m and
n are different from those associated with the
problem that has just been defined. You have probably loaded a file
that belongs to another problem.
Remember, if you have added rows or columns to
a(*),
ha(*) and
ka(*), you will have to alter
m and
n and the map
beginning on the third line (a hazardous operation). It may be
easier to restart with a PUNCH or DUMP file from an earlier
version of the problem.
31 EXIT – the basis file state vector does not match this problem
For some reason, the OLD BASIS file is incompatible with
the present problem, or is not consistent within itself. The number
of basic entries in the state vector (i.e., the number of
3's in
the map) is not the same as
m on the first line, or some of the
2's in the map did not have a corresponding “
j
xj” entry following the map.
32 EXIT – system error. Wrong no. of basic variables: nnn
This exit should never happen. It may indicate that the wrong
MINOS source files have been compiled, or incorrect parameters
have been used in the call to subroutine
minoss.
Check that all integer variables and arrays are declared
integer
in your calling program (including those beginning with
h!), and
that all “real” variables and arrays are declared consistently.
(They should be
double precision on most machines.)
| The following messages arise if additional storage is needed
to
allow optimization to begin. The problem is abandoned. |
The main character storage array
cw(*) is not large
enough.
43 EXIT – not enough integer storage to start solving the problem
The main integer storage array
iw(*) is not large
enough to provide workspace for the optimization procedure. See the
advice given for Exit 20.
44 EXIT – not enough real storage to start solving the problem
The main storage array
rw(*) is not large enough to
provide workspace for the optimization procedure. Be sure that the
Superbasics limit is not unreasonably large. Otherwise, see the
advice for EXIT 20.
6.3.7 Solution output
At the end of a run, the final solution is output to the PRINT
file in accordance with the
Solution keyword. Some header
information appears first to identify the problem and the final
state of the optimization procedure. A ROWS section and a COLUMNS
section then follow, giving one line of information for each row and
column. The format used is similar to certain commercial systems,
though there is no industry standard.
An example of the printed solution is given in
§
6.3. In general, numerical values are output
with format
f16.5. The maximum record length is 111 characters,
including the first (carriage-control) character.
To reduce clutter, a dot “
.” is printed for any numerical
value that is exactly zero. The values ±1 are also printed
specially as
1.0 and
-1.0. Infinite bounds (±10
20
or larger) are printed as
None.
Note: If two problems are the same except that one minimizes
an objective
f(
x) and the other maximizes −
f(
x), their solutions
will be the same but the signs of the dual variables π
i and the
reduced gradients
dj will be reversed.
The ROWS section
General linear constraints take the form
l ≤
Ax ≤
u. The
ith
constraint is therefore of the form
α ≤ aT x ≤ β,
and the value of
aT x is called the
row activity.
Internally, the linear constraints take the form
Ax −
s = 0, where
the slack variables
s should satisfy the bounds
l ≤
s ≤
u.
For the
ith “row", it is the slack variable
si that is
directly available, and it is sometimes convenient to refer to its
state. Slacks may be basic or nonbasic (but not superbasic).
Nonlinear constraints α ≤
Fi(
x) +
aT x ≤ β are
treated similarly, except that the row activity and degree of
infeasibility are computed directly from
Fi(
x) +
aT x rather
than from
si.
-
Label
- Description
- Number
-
The value n+i. This is the internal number used to refer
to the ith slack in the iteration log.
- Row
-
The name of the ith row.
- State
-
The state of the ith row relative to the bounds α
and β. The various states possible are as follows.
- State = LL
- The row is at its lower limit, α.
- State = UL
- The row is at its upper limit, β.
- State = EQ
- The limits are the same (α = β).
- State = BS
- The constraint is not binding. si is basic.
-
-
A key is sometimes printed before the State to give some
additional information about the state of the slack variable.
- State key = A
- Alternative optimum possible. The
slack is nonbasic, but its reduced gradient is
essentially zero. This means that if the slack were
allowed to start moving from its current value, there
would be no change in the objective function.
The values of the basic and superbasic
variables might change, giving a genuine
alternative solution. The values of the dual variables
might also change.
- State key = D
- Degenerate. The slack is basic, but it is
equal to (or very close to) one of its bounds.
- State key = I
- Infeasible. The slack is basic and is
currently violating one of its bounds by more than
the Feasibility tolerance.
- State key = N
- Not precisely optimal. The slack is nonbasic.
Its reduced gradient is larger than the
Optimality tolerance .
-
-
Note: If Scale option > 0, the tests for
assigning A, D, I, N are
made on the scaled problem, since the keys are then
more likely to be meaningful.
- Activity
-
The row value aT x (or Fi(x) + aT x for nonlinear rows).
- Slack activity
-
The amount by which the row differs from its nearest bound.
(For free rows, it is taken to be minus the Activity.)
- Lower limit
-
α, the lower bound on the row.
- Upper limit
-
β, the upper bound on the row.
- Dual activity
-
The value of the dual variable πi, often called the
shadow price (or simplex multiplier) for the ith
constraint. The full vector π always satisfies BT π
= gB, where B is the current basis matrix and gB
contains the associated gradients for the current objective
function.
- I
-
The constraint number, i.
The COLUMNS section
Here we talk about the “column variables"
xj,
j = 1:
n. We
assume that a typical variable has bounds α ≤
xj ≤
β.
-
Label
- Description
- Number
-
The column number, j. This is the internal number used to refer
to xj in the iteration log.
- Column
-
The name of xj.
- State
-
The state of xj relative to the bounds α and
β. The various states possible are as follows.
- State = LL
- xj is nonbasic at its lower limit, α.
- State = UL
- xj is nonbasic at its upper limit, β.
- State = EQ
- xj is nonbasic and fixed at the value α =
β.
- State = FR
- xj is nonbasic at some value strictly between
its bounds: α < xj < β.
- State = BS
- xj is basic. Usually α < xj < β.
- State = SBS
- xj is superbasic. Usually α < xj < β.
-
-
A key is sometimes printed before the State to give some
additional information about the state of xj.
- State key = A
- Alternative optimum possible. The
variable is nonbasic, but its reduced gradient is
essentially zero. This means that if xj were
allowed to start moving from its current value, there
would be no change in the objective function.
The values of the basic and superbasic
variables might change, giving a genuine
alternative solution. The values of the dual variables
might also change.
- State key = D
- Degenerate. xj is basic, but it is
equal to (or very close to) one of its bounds.
- State key = I
- Infeasible. xj is basic and is
currently violating one of its bounds by more than
the Feasibility tolerance.
- State key = N
- Not precisely optimal. xj is nonbasic.
Its reduced gradient is larger than the
Optimality tolerance .
-
-
Note: If Scale option > 0, the tests for
assigning A, D, I, N are
made on the scaled problem, since the keys are then
more likely to be meaningful.
- Activity
-
The value of the variable xj.
- Obj Gradient
-
gj, the jth component of the gradient of the
(linear or nonlinear) objective function.
(If any xj is infeasible, gj is the gradient of the
sum of infeasibilities.)
- Lower limit
-
α, the lower bound on xj.
- Upper limit
-
β, the upper bound on xj.
- Reduced gradnt
-
The reduced gradient dj = gj − πT aj, where aj is
the jth column of the constraint matrix (or the jth
column of the Jacobian at the start of the final major
iteration).
- M+J
-
The value m+j.
6.3.8 The SUMMARY file
If
Summary file > 0, the following information is output to
the SUMMARY file. (It is a brief form of the PRINT file.) All
output lines are less than 72 characters.
| • |
The Begin line from the SPECS file, if any. |
| • |
The basis file loaded, if any. |
| • |
A brief Major iteration log. |
| • |
A brief Minor iteration log. |
| • |
The EXIT condition and a summary of the final solution. |
The following SUMMARY file is from example problem
t6wood
using
Print level 0 and
Major damping parameter 0.5.
==============================
M I N O S 5.51 (Nov 2002)
==============================
Begin t6wood (WOPLANT test problem; optimal obj = -15.55716)
Name WOPLANT
===> Note: row OBJ selected as linear part of objective.
Rows 9
Columns 12
Elements 73
Scale option 2, Partial price 1
Itn 0 -- linear constraints satisfied.
This is problem t6wood. Derivative level = 3
funcon sets 36 out of 50 constraint gradients.
Major minor step objective Feasible Optimal nsb ncon penalty BSwap
1 0T 0.0E+00 0.00000E+00 5.9E-01 1.1E+01 0 4 1.0E+00 0
2 22 5.0E-01 -1.56839E+01 2.7E-01 1.6E+01 3 47 1.0E+00 0
3 10 6.0E-01 -1.51527E+01 1.5E-01 9.9E+00 2 68 1.0E+00 2
4 21 5.7E-01 -1.53638E+01 6.4E-02 3.6E+00 3 113 1.0E+00 1
5 15 1.0E+00 -1.55604E+01 2.7E-02 1.4E-01 3 144 1.0E+00 0
6 5 1.0E+00 -1.55531E+01 6.4E-03 2.2E-01 3 154 1.0E+00 0
7 4 1.0E+00 -1.55569E+01 3.1E-04 7.0E-04 3 160 1.0E-01 0
8 2 1.0E+00 -1.55572E+01 1.6E-08 1.1E-04 3 163 1.0E-02 0
9 1 1.0E+00 -1.55572E+01 5.1E-14 2.2E-06 3 165 1.0E-03 0
EXIT -- optimal solution found
Problem name WOPLANT
No. of iterations 80 Objective value -1.5557160112E+01
No. of major iterations 9 Linear objective -1.5557160112E+01
Penalty parameter 0.000100 Nonlinear objective 0.0000000000E+00
No. of calls to funobj 0 No. of calls to funcon 165
No. of superbasics 3 No. of basic nonlinears 6
No. of degenerate steps 0 Percentage 0.00
Norm of x (scaled) 9.8E-01 Norm of pi (scaled) 1.8E+02
Norm of x 3.2E+01 Norm of pi 1.6E+01
Max Prim inf(scaled) 0 0.0E+00 Max Dual inf(scaled) 1 2.2E-06
Max Primal infeas 0 0.0E+00 Max Dual infeas 1 5.8E-08
Nonlinear constraint violn 5.1E-14
Solution printed on file 9
funcon called with nstate = 2
Time for MPS input 0.00 seconds
Time for solving problem 0.04 seconds
Time for solution output 0.00 seconds
Time for constraint functions 0.00 seconds
Time for objective function 0.00 seconds
Endrun
« Previous « Start » Next »
 π
π , a
measure of the size of the current π.)
, a
measure of the size of the current π.)d S
is sufficiently small, compute some or all of the reduced costs d N = g N − NTπ to determine if a favorable nonbasic column aq exists. If so, move that column from N into S, expanding R accordingly.
 d S
d S ≤ δopt
≤ δopt π
π and the reduced
costs (component of d N) are all sufficiently positive or
negative, as judged by the same quantity δopt
and the reduced
costs (component of d N) are all sufficiently positive or
negative, as judged by the same quantity δopt π
π .
. ≤
PT2 − P02,
≤
PT2 − P02,
















 π
π ≥ −t or dj /
≥ −t or dj /  π
π ≤ t respectively, and if
|dj| /
≤ t respectively, and if
|dj| /  π
π ≤ t for superbasic variables.
≤ t for superbasic variables. π
π is a measure of the size of the dual
variables. It is included to make the tests independent of a large
scale factor on the objective function. The quantity actually used
is defined by σ = Σi=1m |πi|,
is a measure of the size of the dual
variables. It is included to make the tests independent of a large
scale factor on the objective function. The quantity actually used
is defined by σ = Σi=1m |πi|,  π
π =
max{σ / √m, 1.0} , so that only scale factors larger
than 1.0 are allowed for. If the objective is scaled down to be very
small, the optimality test reduces to comparing dj against
t.
=
max{σ / √m, 1.0} , so that only scale factors larger
than 1.0 are allowed for. If the objective is scaled down to be very
small, the optimality test reduces to comparing dj against
t. p
p are ignored.
are ignored.



 x
x ) /
) /  p
p , and the first evaluation of F(x) is
at the potentially smaller steplength α1 = min(1, β,
β).
, and the first evaluation of F(x) is
at the potentially smaller steplength α1 = min(1, β,
β). ZT g0
ZT g0 . (In fact, the norm is |dj|, the size of the
reduced gradient for the new superbasic variable xj.)
. (In fact, the norm is |dj|, the size of the
reduced gradient for the new superbasic variable xj.) ZT g
ZT g ≤ t ×
≤ t ×
 ZT g0
ZT g0 . (
. ( ZT g
ZT g is the size of the largest
reduced-gradient among the superbasic variables.)
is the size of the largest
reduced-gradient among the superbasic variables.) π
π . Only the tolerance t can be altered at
run-time.
. Only the tolerance t can be altered at
run-time.