« Previous « Start » Next »
7 SQOPT details
7.1 Introduction
TOMVIEW /SQOPT (hereafter referred to as SQOPT ) is a program for solving the
large-scale
linear or quadratic programming problem, which is
assumed to be stated in following form:
where
l and
u are constant lower and upper bounds, and
A is a
sparse matrix and
q(
x) is a linear or quadratic function objective
function that may be specified in a variety of ways, depending upon
the particular problem being solved. The optional parameter
maximize may be used to specify a problem in which
q is
maximized instead of minimized.
Upper and lower bounds are specified for all variables and constraints.
This form allows full generality in specifying various types of
constraint. In particular, the
jth constraint may be defined as
an
equality by setting
lj =
uj. If certain bounds are
not present, the associated elements of
l or
u may be set to
special values that are treated as −∞ or +∞.
The possible forms for the function
q(
x) are summarized in
Table
3. The most general form for
q(
x) is
| q(x) = f + |
|
cj xj
+ |
|
|
|
|
xi Hij xj
= f + cT x + |
|
xT H x,
|
where
f is a constant,
c is a constant
n vector and
H is a
constant symmetric
n×
n matrix with elements {
Hij}. In
this form,
q is a quadratic function of
x and Problem LCQP is
known as a
quadratic program (QP). SQOPT is suitable for
all
convex quadratic programs. The defining feature of a
convex QP is that the matrix
H must be
positive
semidefinite—i.e., it must satisfy
xT H x ≥ 0 for all
x.
If not,
q(
x) is nonconvex and SQOPT will terminate with the
error indicator
inform = 4.
Table 3: Choices for the objective function q(x).
Problem type |
Objective function q |
Hessian matrix |
Quadratic Programming (QP) |
f+cT x+1/2 xT Hx |
Symmetric positive semidefinite |
| Linear Programming (LP) |
f+cT x |
H=0 |
Feasible Point (FP) |
Not Applicable |
f=0, c=0, H=0 |
If
H=0, then
q(
x) =
f +
cT x and the problem is known as a
linear program (LP).
If
H=0,
f=0, and
c=0, there is no objective function and the
problem is a
feasible point problem (FP), which is equivalent
to finding a point that satisfies the constraints on
x. In the
situation where no feasible point exists, several options are
available for finding a point that minimizes the constraint
violations (see the optional parameter
Elastic option).
SQOPT is suitable for large LPs and QPs in which the matrix
A is
sparse—i.e., when there are sufficiently many zero elements
in
A to justify storing them implicitly.
SQOPT exploits structure or sparsity in
H by requiring
H to be defined
implicitly in a subroutine
that computes the product
Hx for any given vector
x. In many
cases, the product
Hx can be computed very efficiently for any
given
x—e.g.,
H may be a sparse matrix, or a sum of matrices
of rank-one.
7.2 Brief description of the method
Here we briefly describe some features of the algorithm used in
SQOPT and introduce some terminology used in the description of
the subroutine and its arguments. For further details, see
§
7.6.
7.2.1 Formulation of the problem
The upper and lower bounds on the
m components of
Ax are said to
define the
general constraints of the problem. Internally
SQOPT converts the general constraints to equalities by
introducing a set of
slack variables s, where
s = (
s1,
s2,...,
sm)
T. For example, the linear constraint 5 ≤ 2
x1 +
3
x2 ≤ +∞ is replaced by 2
x1 + 3
x2 −
s1 = 0 together
with the bounded slack 5≤
s1 ≤ +∞. Problem LCQP can
therefore be rewritten in the following equivalent form
|
|
|
q(x)
subject to A x − s = 0, l ≤ |

 |
|
|
|

 |
≤ u.
(40) |
Since the slack variables
s are subject to the same upper and
lower bounds as the components of
Ax, they allow us to think of
the bounds on
Ax and
x as simply bounds on the combined vector
(
x,
s). (In order to indicate their special role in problem QP, the
original variables
x are sometimes known as “column variables”,
and the slack variables
s are known as “row variables”)
Each LP or QP is solved using an
active-set method. This is an
iterative procedure with two phases: a
phase 1 (sometimes
called the
feasibility phase), in which the sum of
infeasibilities is minimized to find a feasible point; and a
phase 2 (or
optimality phase), in which
q is
minimized by constructing a sequence of iterations that lies within
the feasible region.
Phase 1 involves solving a linear program of the form
|
|
|
|
|
(vj + wj)
subject to A x − s = 0, l ≤ |

 |
|
|
|

 |
−v + w ≤ u, v ≥ 0, w ≥ 0
(41) |
which is equivalent to minimizing the sum of the constraint
violations. If the constraints are feasible (i.e., at least one
feasible point exists), eventually a point will be found at which
both
v and
w are zero. The associated value of (
x,
s) satisfies
the original constraints and is used as the starting point for the
phase 2 iterations for minimizing
q.
If the constraints are infeasible (i.e.,
v 0 or
w 0 at
the end of phase 1), no solution exists for Problem LCQP and the
user has the option of either terminating or continuing in so-called
elastic mode (see the discussion of the optional parameter
Elastic option). In elastic mode, a “relaxed” or
“perturbed” problem is solved in which
q(
x) is minimized while
allowing some of the bounds to become “elastic”—i.e., to change
from their specified values. Variables subject to elastic bounds
are known as
elastic variables. An elastic variable is free
to violate one or both of its original upper or lower bounds.
To make the relaxed problem meaningful, SQOPT minimizes
q while
(in some sense) finding the “smallest” violation of the elastic
variables. In the situation where all the variables are elastic,
the relaxed problem has the form
|
|
|
q(x) + γ |
|
(vj + wj)
subject to A x − s = 0, l ≤ |

 |
|
|
|

 |
−v + w ≤ u, v ≥ 0, w ≥ 0
(42) |
where γ is a nonnegative parameter known as the
elastic
weight, and
q(
x) + γΣ
j(
vj +
wj) is called the
composite objective. In the more general situation where only
a subset of the bounds are elastic, the
v's and
w's for the
non-elastic bounds are fixed at zero.
The
elastic weight can be chosen to make the composite objective
behave like either the original objective
q(
x) or the sum of
infeasibilities. If γ = 0, SQOPT will attempt to minimize
q subject to the (true) upper and lower bounds on the nonelastic
variables (and declare the problem infeasible if the nonelastic
variables cannot be made feasible). At the other extreme, choosing
γ sufficiently large, will have the effect of minimizing the
sum of the violations of the elastic variables subject to the
original constraints on the non-elastic variables. Choosing a large
value of the elastic weight is useful for defining a
“least-infeasible” point for an infeasible problem.
In phase 1 and elastic mode, all calculations involving
v and
w
are done implicitly in the sense that an elastic variable
xj is
allowed to violate its lower bound (say) and an explicit value of
v can be recovered as
vj =
lj −
xj.
7.2.2 The main iteration
A constraint is said to be
active or
binding at
x if
the associated component of either
x or
Ax is equal to one of
its upper or lower bounds. Since an active constraint in
Ax has
its associated slack variable at a bound, we can neatly describe the
status of both simple and general upper and lower bounds in terms of
the status of the variables (
x,
s). A variable is said to be
nonbasic if it is temporarily fixed at its upper or lower
bound. It follows that regarding a general constraint as being
active is equivalent to thinking of its associated slack as
being
nonbasic.
At each iteration of an active-set method, the constraints
A x −
s = 0 are (conceptually) partitioned into the form
Bx B +
Sx S +
N
x N = 0, where
x N comprises the nonbasic components of (
x,
s)
and the
basis matrix B is square and nonsingular. The
elements of
x B and
x S are called the
basic and
superbasic variables respectively; with
x N they are a
permutation of the elements of
x and
s. At a QP solution, the
basic and superbasic variables will lie somewhere between their
bounds, while the nonbasic variables will be equal to one of their
upper or lower bounds. At each iteration,
x S is regarded as a
set of independent variables that are free to move in any desired
direction, namely one that will improve the value of the QP
objective (or sum of infeasibilities). The basis variables are then
adjusted in order to ensure that (
x,
s) continues to satisfy
Ax −
s = 0. The number of superbasic variables (
n S say) therefore
indicates the number of degrees of freedom remaining after the
constraints have been satisfied. In broad terms,
n S is a measure
of
how nonlinear the problem is. In particular,
n S will
always be zero for FP and LP problems.
If it appears that no improvement can be made with the current
definition of
B,
S and
N, a nonbasic variable is selected to
be added to
S, and the process is repeated with the value of
n S
increased by one. At all stages, if a basic or superbasic variables
encounters one of its bounds, the variable is made nonbasic and the
value of
n S is decreased by one.
Associated with each of the
m equality constraints
A x −
s = 0
is a
dual variable π
i. Similarly, each variable in
(
x,
s) has an associated
reduced gradient dj (also known
as a
reduced cost). The reduced gradients for the variables
x are the quantities
g −
ATπ, where
g is the
gradient of the QP objective; and the reduced gradients for the
slacks
s are the dual variables π. The QP subproblem is
optimal if
dj ≥ 0 for all nonbasic variables at their lower
bounds,
dj ≤ 0 for all nonbasic variables at their upper
bounds, and
dj = 0 for all superbasic variables. In practice, an
approximate QP solution is found by slightly relaxing these
conditions on
dj (see the
Optimality tolerance described in
§
7.3.2).
The process of computing and comparing reduced gradients is known as
pricing (a term first introduced in the context of the
simplex method for linear programming). To “price” a nonbasic
variable
xj means that the reduced gradient
dj associated with
the relevant active upper or lower bound on
xj is computed via
the formula
dj =
gj −
ajT π, where
aj is the
jth column
of (
A −
I ). (The variable selected by the price, and its
corresponding value of
dj (i.e., its reduced gradient) are
printed in the columns marked
+SBS and
dj in the
Print file output.) If
A has significantly more columns than
rows (i.e.,
n≫
m), pricing can be computationally expensive. In
this case, a strategy known as
partial pricing can be used to
compute and compare only a subset of the
dj's.
7.3 The SPECS file
The performance of SQOPT is controlled by a number of parameters
or “options". These are normally set in
Prob.SOL.optPar. Each
option has a default value that should be appropriate for most
problems. (The defaults are given in the next section.) For special
situations it is possible to specify non-standard values for some or
all of the options, using data in the following general form:
Begin SQOPT options
Iterations limit 500
Feasibility tolerance 1.0e-7
Scale all variables
End SQOPT options
We shall call such data a SPECS file, since it
specifies various options. The file starts with the keyword
Begin and ends with
End. The file is in free format. Each
line specifies a single option, using one or more items as follows:
-
A keyword (required for all options).
- A phrase (one or more words) that qualifies the keyword
(only for some options).
- A number that specifies an integer or real value
(only for some options). Such numbers may be up to 16
contiguous characters in Fortran 77's I, F, E
or D formats, terminated by a space.
The items may be entered in upper or lower case or a mixture of
both. Some of the keywords have synonyms, and certain abbreviations
are allowed, as long as there is no ambiguity. Blank lines and
comments may be used to improve readability. A comment begins with
an asterisk (
*), which may appear anywhere on a line. All
subsequent characters on the line are ignored.
It may be useful to include a comment on the first (
Begin) line
of the file. This line is echoed to the SUMMARY file.
Most of the options described in the next section should be left at
their default values for any given model. If experimentation is
necessary, we recommend changing just one option at a time.
7.3.1 SPECS File Checklist and Defaults
The following example SPECS file shows all valid
keywords
and their
default values. The keywords are grouped according
to the function they perform.
Some of the default values depend on є, the relative
precision of the machine being used. The values given here
correspond to double-precision arithmetic on most current machines
(є ≈ 2.22× 10
−16). Similar values would
apply to any machine having about 15 decimal digits of precision.
BEGIN checklist of SPECS file parameters and their default values
* Printing
Print level 1 * 1-line iteration log
Print file 15 *
Summary file 6 * typically the screen
Print frequency 1 * iterations log on PRINT file
Summary frequency 1 * iterations log on SUMMARY file
Solution Yes * on the PRINT file
* Suppress options listing * default: options are listed
* Convergence Tolerances
Feasibility tolerance 1.0e-6 * for satisfying the simple bounds
Optimality tolerance 1.0e-6 * target value for reduced gradients
* Scaling
Scale option 2 * All constraints and variables
Scale tolerance 0.9 *
* Scale Print * default: scales are not printed
* Other Tolerances
Crash tolerance 0.1 *
LU factor tolerance 10.0 * limits size of multipliers in
L
LU update tolerance 10.0 * the same during updates
LU singularity tolerance 2.0e-6 *
Pivot tolerance 3.7e-11 * є
2/3
* LP/QP problems
Crash option 0 * all slack initial basis
Elastic weight 1.0 * used only during elastic mode
Iterations limit 10000 * or
m if that is more
Minimize * (opposite of
Maximize)
Partial price 1 * 10 for large LPs
Superbasics limit 500 * or
n1+1 if that is less
Reduced Hessian dimension 500 * or
Superbasics limit
Unbounded step size 1.0e+18 *
* Infeasible problems
Elastic weight 100 * used only during elastic mode
Elastic mode 1 * use elastic mode when infeasible
Elastic objective 2 * infinite weight on the elastics
* Frequencies
Check frequency 60 * test row residuals
 Ax
Ax −
s
Expand frequency 10000 * for anti-cycling procedure
Factorization frequency 100 *
Save frequency 100 * save basis map
7.3.2 Description of the optional parameters
The following is an alphabetical list of the options that may appear
in the SPECS file, and a description of their effect.
Option: Check frequency k 60
Every
kth iteration after the most recent basis factorization, a
numerical test is made to see if the current solution
x satisfies
the general constraints. The constraints are of the form
Ax −
s =
0, where
s is the set of slack variables. To perform the
numerical test, the residual vector
r =
s −
Ax is computed. If
the largest component of
r is judged to be too large, the current
basis is refactorized and the basic variables are recomputed to
satisfy the general constraints more accurately.
Check frequency 1 is useful for debugging purposes, but
otherwise this option should not be needed.
Option: Crash option i 0
Option: Crash tolerance r 0.1
Except on restarts, a CRASH procedure is used to select an
initial basis from certain rows and columns of the constraint matrix
(
A −
I ). The
Crash option i determines which rows and
columns of
A are eligible initially, and how many times CRASH
is called. Columns of −
I are used to pad the basis where
necessary.
-
i Meaning
- 0 The initial basis contains only slack variables: B = I.
- 1 CRASH is called once, looking for a triangular basis in
all rows and columns of the matrix A.
- 2 CRASH is called once, looking for a triangular basis in linear rows.
- 3 CRASH is called twice. The two calls treat linear
equalities and linear inequalities separately.
If
i ≥ 1, certain slacks on inequality rows are selected for the
basis first. (If
i ≥ 2, numerical values are used to exclude
slacks that are close to a bound.) CRASH then makes several
passes through the columns of
A, searching for a basis matrix that
is essentially triangular. A column is assigned to “pivot" on a
particular row if the column contains a suitably large element in a
row that has not yet been assigned. (The pivot elements ultimately
form the diagonals of the triangular basis.) For remaining
unassigned rows, slack variables are inserted to complete the basis.
The
Crash tolerance r allows the starting procedure CRASH
to ignore certain “small" nonzeros in each column of
A. If
amax is the largest element in column
j, other nonzeros
aij in the column are ignored if |
aij| ≤
amax
×
r. (To be meaningful,
r should be in the range 0 ≤
r <
1.)
When
r > 0.0, the basis obtained by CRASH may not be strictly
triangular, but it is likely to be nonsingular and almost
triangular. The intention is to obtain a starting basis containing
more columns of
A and fewer (arbitrary) slacks. A feasible
solution may be reached sooner on some problems.
For example, suppose the first
m columns of
A form the matrix
shown under
LU factor tolerance; i.e., a tridiagonal matrix with
entries −1, 4, −1. To help CRASH choose all
m columns for
the initial basis, we would specify
Crash tolerance r for some
value of
r > 1/4.
Option: Elastic mode i 1
This parameter determines if (and when) elastic mode is to be
started. Three elastic modes are available as follows:
-
i Meaning
- 0 Elastic mode is never invoked. SQOPT will terminate as
soon as infeasibility is detected. There may be other points
with significantly smaller sums of infeasibilities.
- 1 Elastic mode is invoked only if the constraints are found
to be infeasible (the default). If the constraints are
infeasible, continue in elastic mode with the composite
objective determined by the values of Elastic objective
and Elastic weight.
- 2 The iterations start and remain in elastic mode. This
option allows you to minimize the composite objective
function directly without first performing phase-1
iterations.
The success of this option will depend critically on your
choice of Elastic weight. If Elastic weight is
sufficiently large and the constraints are feasible, the
minimizer of the composite objective and the solution of the
original problem are identical. However, if the Elastic
weight is not sufficiently large, the minimizer of the
composite function may be infeasible, even though a feasible
point for the constraints may exist.
Option: Elastic objective i 2
This option determines the form of the composite objective. Three
types of composite objectives are available.
-
i Meaning
- 0 Include only the true objective q(x) in the composite
objective. This option sets γ = 0 in the composite
objective and will allow SQOPT to ignore the elastic bounds
and find a solution that minimizes q subject to the
nonelastic constraints. This option is useful if there are
some “soft” constraints that you would like to ignore if
the constraints are infeasible.
- 1 Use a composite objective defined with γ determined
by the value of Elastic weight. This value is intended to
be used in conjunction with Elastic mode = 2.
- 2 Include only the elastic variables in the composite
objective. The elastics are weighted by γ = 1. This
choice minimizes the violations of the elastic variable at
the expense of possibly increasing the true objective. This
option can be used to find a point that minimizes the sum of
the violations of a subset of constraints determined by the
parameter helast.
Option: Elastic weight r 1.0
This keyword defines the value of γ in the composite
objective.
Option: Expand frequency i 10000
This option is part of the EXPAND anti-cycling procedure
[
3] designed to make progress even on highly degenerate
problems.
The strategy is to force a positive step at every iteration, at the
expense of violating the bounds on the variables by a small amount.
Suppose that the
Feasibility tolerance is δ. Over a
period of
i iterations, the tolerance actually used by SQOPT
increases from 0.5δ to δ (in steps of 0.5δ/
i).
Increasing
i helps reduce the number of slightly infeasible nonbasic
basic variables (most of which are eliminated during a resetting
procedure). However, it also diminishes the freedom to choose a
large pivot element (see
Pivot tolerance).
Option: Factorization Frequency k 100 (LP) or 50 (QP)
At most
k basis changes will occur between factorizations of the
basis matrix.
-
With linear programs, the basis factors are usually updated
every iteration. The default k is reasonable for typical
problems. Higher values up to k=100 (say) may be
more efficient on problems that are extremely sparse and well
scaled.
- When the objective function is quadratic, fewer basis
updates will occur as an optimum is approached. The number
of iterations between basis factorizations will therefore
increase. During these iterations a test is made regularly
(according to the Check frequency) to ensure that the
general constraints are satisfied. If necessary the basis
will be refactorized before the limit of k updates is
reached.
Option: Feasibility tolerance t 1.0E−6
A
feasible problem is one in which all variables satisfy
their upper and lower bounds to within the absolute tolerance
t.
(This includes slack variables. Hence, the general constraints are
also satisfied to within
t.)
-
SQOPT attempts to find a feasible point for the non-elastic
constraints before optimizing the objective. If the sum of the
infeasibilities of these constraints cannot be reduced to zero,
the problem is declared INFEASIBLE. If sInf is quite
small, it may be appropriate to raise t by a factor of 10 or
100. Otherwise, some error in the data should be suspected.
- Note: if sInf is not small and you have not asked
SQOPT to minimize the violations of the elastic variables
(i.e., you have not specified Elastic objective =
2, there may be other points that have a significantly
smaller sum of infeasibilities. SQOPT will not attempt
to find the solution that minimizes the sum unless
Elastic objective = 2.
- If scale is used, feasibility is defined in terms of the
scaled problem (since it is then more likely to be
meaningful).
Option: Infinite Bound Size r 1.0E+20
If
r > 0,
r defines the “infinite” bound
BigBnd in the
definition of the problem constraints. Any upper bound greater than
or equal to
BigBnd will be regarded as plus infinity (and
similarly for a lower bound less than or equal to −
BigBnd).
If
r ≤ 0, the default value is used.
Option: Iterations Limit k 3*
m
This is the maximum number of iterations of the simplex method or
the QP reduced-gradient algorithm allowed.
-
Itns is an alternative keyword.
- k = 0 is valid. Both feasibility and optimality are checked.
Option: Log Frequency k 1
Option: see Print Frequency
Option: LU factor tolerance r1 100.0
Option: LU update tolerance r2 10.0
These tolerances affect the stability and sparsity of the basis
factorization
B =
LU during refactorization and updating,
respectively. They must satisfy
r1,
r2 ≥ 1.0. The matrix
L
is a product of matrices of the form
where the multipliers μ satisfy |μ| ≤
ri. Smaller values
of
ri favor stability, while larger values favor sparsity. The
default values usually strike a good compromise.
-
For large and relatively dense problems, r1 = 10.0 or 5.0
(say) may give a useful improvement in stability without impairing
sparsity to a serious degree.
- For certain very regular structures (e.g., band matrices) it may
be necessary to reduce r1 and/or r2 in order to achieve
stability. For example, if the columns
of A include a submatrix of the form







 |
|
| 4 |
−1 |
| −1 |
4 |
−1 |
| |
−1 |
4 |
−1 |
| |
|
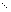 |
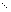 |
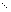 |
| |
|
|
−1 |
4 |
−1 |
| |
|
|
|
−1 |
4 |
|
|







 |
, |
Option: LU singularity tolerance r_3 є^2/3
This tolerance should satisfy
r3 ≤ є
1/4 ≈
10
−4. It helps guard against ill-conditioned basis matrices.
When the
LU factors of
B are computed directly (not updated),
the diagonal elements of
U are tested as follows: if |
Ujj| ≤
r3 or |
Ujj| <
r3 max
i |
Uij|, the
j-th column of the
basis is replaced by the corresponding slack variable.
(Replacements are rare because the
LU updating method is stable.
They are most likely to occur during the first factorization.)
Option: LU density tolerance r1 0.6
Option: LU singularity tolerance r2 є
2/3≈ 10
−11
The density tolerance
r1 is used during
LU factorization of the
basis matrix. Columns of
L and rows of
U are formed one at a
time, and the remaining rows and columns of the basis are altered
appropriately. At any stage, if the density of the remaining matrix
exceeds
r1, the Markowitz strategy for choosing pivots is altered
to reduce the time spent searching for each remaining pivot.
Raising the density tolerance towards 1.0 may give slightly sparser
LU factors, with a slight increase in factorization time.
The singularity tolerance
r2 helps guard against ill-conditioned
basis matrices. When the basis is refactorized, the diagonal
elements of
U are tested as follows: if |
Ujj| ≤
r2 or
|
Ujj| <
r2 max
i |
Uij|, the
jth column of the basis is
replaced by the corresponding slack variable. (This is most likely
to occur after a restart, or at the start of a major iteration.)
Option: Minimize
Option: Maximize
This specifies the required direction of optimization. It applies
to both linear and quadratic terms in the objective.
Option: Optimality tolerance t 1.0e−6
This is used to judge the size of the reduced gradients
dj =
gj−π
T aj, where
gj is the
jth component of the gradient,
aj is the associated column of the constraint matrix
tmatA−
I, and π is the set of dual variables.
Option: Partial Price i 10 (LP) or 1 (QP)
This parameter is recommended for large problems that have
significantly more variables than constraints. It reduces the work
required for each “pricing" operation (when a nonbasic variable is
selected to become superbasic).
-
When i=1, all columns of the constraint matrix ( A −I )
are searched.
- Otherwise, A and I are partitioned to give i roughly
equal segments Aj, Ij (j = 1 to i). If the previous
pricing search was successful on Aj, Ij, the next
search begins on the segments Aj+1, Ij+1. (All
subscripts here are modulo i.)
- If a reduced gradient is found that is larger than some
dynamic tolerance, the variable with the largest such reduced
gradient (of appropriate sign) is selected to become
superbasic. If nothing is found, the search continues on the
next segments Aj+2, Ij+2, and so on.
- Partial price t (or t/2 or t/3) may be appropriate
for time-stage models having t time periods.
Option: Pivot Tolerance r є
2/3
Broadly speaking, the pivot tolerance is used to prevent columns
entering the basis if they would cause the basis to become almost
singular.
-
When x changes to x + α p for some search
direction p, a “ratio test" is used to determine which component
of x reaches an upper or lower bound first. The corresponding
element of p is called the pivot element.
- For linear problems, elements of p are ignored (and therefore
cannot be pivot elements) if they are smaller than the pivot
tolerance r.
- It is common for two or more variables to reach a bound at
essentially the same time. In such cases, the Feasibility tolerance (say t) provides some freedom to
maximize the pivot element and thereby improve numerical
stability. Excessively small values of t should
therefore not be specified.
- To a lesser extent, the Expand frequency (say f) also
provides some freedom to maximize the pivot element.
Excessively large values of f should therefore not be
specified.
Option: Print frequency k 1
One line of the iteration log will be printed every
kth iteration.
A value such as
k=
10 is suggested for those interested only
in the final solution.
Option: Print level k 1
This controls the amount of printing produced by SQOPT as
follows.
-
≥0 No output except error messages. If you want to
suppress all output, set Print file = 0.
- ≥ 1 The set of selected options (including workspace limits),
problem statistics, summary of the scaling procedure, information about
the initial basis resulting from a CRASH or a BASIS file. A single
line of output each iteration (controlled by Print frequency), and
the exit condition with a summary of the final solution.
- ≥ 10 Basis factorization statistics.
Option: Save frequency k 100
If a NEW BASIS file has been specified, a basis map describing the
current solution will be saved on the appropriate file every
kth
iteration. A BACKUP BASIS file will also be saved if specified.
Option: Scale option i 2 (LP) or 1 (QP)
Option: Scale tolerance r 0.9
Option: Scale Print
Three scale options are available as follows:
-
i Meaning
- 0 No scaling. This is recommended if it is known that x and
the constraint matrix never have very large elements (say,
larger than 1000).
- 1 The constraints and variables are scaled by an iterative
procedure that attempts to make the matrix coefficients as close
as possible to 1.0 (see Fourer [11]). This will
sometimes improve the performance of the solution procedures.
- 2 The constraints and variables are scaled by the iterative
procedure. Also, a certain additional scaling is performed that
may be helpful if the right-hand side b or the solution x is
large. This takes into account columns of ( A −I ) that
are fixed or have positive lower bounds or negative upper
bounds.
Scale tolerance affects how many passes might be needed through the
constraint matrix. On each pass, the scaling procedure computes the
ratio of the largest and smallest nonzero coefficients in each
column:
| ρj = |
|
|aij| / |
|
|aij| (aij 0).
|
If max
j ρ
j is less than
r times its previous value,
another scaling pass is performed to adjust the row and column
scales. Raising
r from 0.9 to 0.99 (say) usually increases the
number of scaling passes through
A. At most 10 passes are made.
Scale Print causes the row-scales
r(
i) and column-scales
c(
j) to be printed. The scaled matrix coefficients are
3
aij =
aij c(
j) /
r(
i), and the scaled bounds on the
variables and slacks are
2
lj =
lj /
c(
j), 3
uj =
uj /
c(
j),
where
c(
j) ≡
r(
j−
n) if
j>
n.
Option: Solution Yes
Option: Solution No
Option: Solution If Optimal, Infeasible, or Unbounded
Option: Summary file f 6
Option: Summary frequency k 100
If
f>0, a brief log will be output to file
f, including one line
of information every
kth iteration. In an interactive
environment, it is useful to direct this output to the terminal, to
allow a run to be monitored on-line. (If something looks wrong, the
run can be manually terminated.) Further details are given in
§
7.5.1.
Option: Superbasics limit i min{500,
n1+1}
This places a limit on the storage allocated for superbasic
variables. Ideally,
i should be set slightly larger than the
“number of degrees of freedom" expected at an optimal solution.
For linear programs, an optimum is normally a basic solution with no
degrees of freedom. (The number of variables lying strictly between
their bounds is no more than
m, the number of general
constraints.) The default value of
i is therefore 1.
For quadratic problems, the number of degrees of freedom is often
called the “number of independent variables".
-
Normally, i need not be greater than ncolH+1, where
ncolH is the number of leading nonzero columns of H.
- For many problems, i may be considerably smaller than
ncolH. This will save storage if ncolH is very
large.
- This parameter also sets the Reduced Hessian dimension,
unless the latter is specified explicitly (and conversely).
Option: Unbounded Step Size α
max 1.0E+18
This parameter is intended to detect unboundedness in a quadratic
problem. (It may or may not achieve that purpose!) During a line
search,
q is evaluated at points of the form
x + α
p, where
x and
p are fixed and α varies. if α exceeds
α
max, iterations are terminated with the exit message
problem is unbounded.
Note that unboundedness in
x is best avoided by placing finite
upper and lower bounds on the variables.
7.4 File Output
The following information is output to the PRINT file during the
solution of each problem referred to in the SPECS file.
-
A listing of the relevant part of the SPECS file.
- A listing of the parameters that were or could have been set in the
SPECS file.
- An estimate of the amount of working storage needed, compared to
how much is available.
- Some statistics about the problem.
- The amount of storage available for the LU factorization
of the basis matrix.
- A summary of the scaling procedure, if Scale was specified.
- Notes about the initial basis resulting from a CRASH procedure
or a BASIS file.
- The iteration log.
- Basis factorization statistics.
- The EXIT condition and some statistics about the solution
obtained.
- The printed solution, if requested.
The last four items are described in the following sections. Further
brief output may be directed to the SUMMARY file, as discussed in
§
7.5.1.
7.4.1 The iteration Log
If
Print level > 0, one line of information is output to the
PRINT file every
kth iteration, where
k is the specified
Print frequency (default
k=
1). A heading is printed
before the first such line following a basis factorization. The
heading contains the items described below. In this description, a
PRICE operation is defined to be the process by which one or more
nonbasic variables are selected to become superbasic (in addition to
those already in the superbasic set). The variable selected will be
denoted by
jq. If the problem is purely linear, variable
jq
will usually become basic immediately (unless it should happen to
reach its opposite bound and return to the nonbasic set).
If
Partial price is in effect, variable
jq is selected from
App or
Ipp, the
ppth segments of the
constraint matrix (
A −
I ).
-
Label
-
Description
- Itn
-
The current iteration number.
- pp
-
The Partial Price indicator. The variable selected by the
last PRICE operation came from the ppth partition of A
and −I. pp is set to zero when the basis is refactored.
- dj
-
This is dj, the reduced cost (or reduced gradient) of the
variable jq selected by PRICE at the start of the present
iteration. Algebraically, dj is dj=gj − πT aj for
j=jq, where gj is the gradient of the current
objective function, π is the vector of dual variables, and
aj is the jth column of the constraint matrix
( A −I ).
Note that dj is the norm of the reduced-gradient vector at
the start of the iteration, just after the PRICE operation.
- +SBS
-
The variable jq selected by PRICE to be added to the
superbasic set.
- -SBS
-
The variable chosen to leave the set of superbasics. It has become
basic if the entry under -B is nonzero; otherwise it has become
nonbasic.
- -BS
-
The variable removed from the basis (if any) to become nonbasic.
- -B
-
The variable removed from the basis (if any) to swap with a
slack variable made superbasic by the latest PRICE. The swap
is done to ensure that there are no superbasic slacks.
- Step
-
The step length α taken along the current search
direction p. The variables x have just been changed to x
+ α p. If a variable is made superbasic during the
current iteration (i.e., +SBS is positive), Step will
be the step to the nearest bound. During phase 2, the step can
be greater than one only if the reduced Hessian is not positive
definite.
- Pivot
-
If column aq replaces the rth column of the basis B,
Pivot is the rth element of a vector y satisfying
By = aq. Wherever possible, Step is chosen to avoid
extremely small values of Pivot (since they cause the
basis to be nearly singular). In rare cases, it may be
necessary to increase the Pivot tolerance to exclude very
small elements of y from consideration during the computation
of Step.
- L
-
The number of nonzeros representing the basis factor L.
Immediately after a basis factorization B = LU, this is
lenL, the number of subdiagonal elements in the columns of a
lower triangular matrix. Further nonzeros are added to L
when various columns of B are later replaced. (Thus, L
increases monotonically.)
- U
-
The number of nonzeros in the basis factor U. Immediately
after a basis factorization, this is lenU, the number of
diagonal and superdiagonal elements in the rows of an
upper-triangular matrix. As columns of B are replaced, the
matrix U is maintained explicitly (in sparse form). The value
of U may fluctuate up or down; in general it will tend to
increase.
- ncp
-
The number of compressions required to recover storage in the
data structure for U. This includes the number of
compressions needed during the previous basis factorization.
Normally ncp should increase very slowly. If not, the
amount of integer and real workspace available to SQOPT should
be increased by a significant amount. As a suggestion, the work
arrays iw(*) and rw(*) should be extended by
L+U elements.
- nInf
-
The number of infeasibilities before the present
iteration. This number will not increase unless the iterations
are in elastic mode.
- Sinf,Objective
-
If nInf>0, this is sInf, the sum of infeasibilities
before the present iteration. (It will usually decrease at
each nonzero Step, but if nInf decreases by 2 or more,
sInf may occasionally increase. However, in elastic mode,
it will decrease monotonically.)
Otherwise, it is the value of the current objective function
after the present iteration.
Note: If Elastic mode = 2, the heading is Composite
Obj.
The following items are printed if the problem is a QP or
if the superbasic set is non-empty (i.e., if the current solution is
nonbasic).
-
Label
-
Description
- Norm rg
-
This quantity is rg, the norm of the reduced-gradient
vector at the start of the iteration. (It is the Euclidean norm
of the vector with elements dj for variables j in the
superbasic set. During phase 2 this norm will be approximately
zero after a unit step.
- nS
-
The current number of superbasic variables.
- Cond Hz
-
An estimate of the condition number of the reduced Hessian. It
is the square of the ratio of the largest and smallest
diagonals of the upper triangular matrix R. This constitutes
a lower bound on the condition number of the reduced Hessian
RTR.
To guard against high values of cond Hz, attention should
be given to the scaling of the variables and the constraints.
7.4.2 Basis Factorization Statistics
When
Print Level≥ 20 and
Print file > 0, the
following lines of intermediate printout (< 120 characters) are
produced on the unit number specified by
Print file whenever the
matrix
B or
BS = (
B S )
T is factorized. Gaussian
elimination is used to compute an
LU factorization of
B or
BS, where
PLPT is a lower triangular matrix and
PUQ is an
upper triangular matrix for some permutation matrices
P and
Q.
This factorization is stabilized in the manner described under
LU
factor tolerance in §
7.3.2.
-
Label
-
Description
- Factorize
-
The number of factorizations since the start of the run.
- Demand
-
A code giving the reason for the present factorization.
- Demand Code
-
Meaning
- Demand = 0
-
First LU factorization.
- Demand = 1
-
Number of updates reached the value of the optional parameter
Factorization Frequency.
- Demand = 2
-
Excessive non-zeros in updated factors.
- Demand = 7
-
Not enough storage to update factors.
- Demand = 10
-
Row residuals too large (see the description for Check
Frequency).
- Demand = 11
-
Ill-conditioning has caused inconsistent results.
- Iteration
-
The current iteration number.
- Infeas
-
The number of infeasibilities at the start of the previous
iteration.
- Objective
-
If Infeas>0, this is the sum of infeasibilities at
the start of the previous iteration.
If Infeas=0, this is the value of the objective
function after the previous iteration.
- Nonlinear
-
The number of nonlinear variables in the current basis B.
(not printed if B S is factorized).
- Linear
-
The number of linear variables in B.
(not printed if B S is factorized).
- Slacks
-
The number of slack variables in B. (not printed if B S is
factorized).
- Elems
-
The number of nonzero matrix elements in B. (not printed if
B S is factorized).
- Density
-
The percentage nonzero density of B, 100×
Elems/(m×m), where m is the number
of rows in the problem (m = Linear +
Slacks).
- Comprssns
-
The number of times the data structure holding the partially
factored matrix needed to be compressed, to recover unused
storage. Ideally this number should be zero. If it is more
than 3 or 4, the amount of workspace available to SQOPT should
be increased for efficiency.
- Merit
-
The average Markowitz merit count for the elements chosen to be
the diagonals of PUQ. Each merit count is defined to be
(c−1)(r−1) where c and r are the number of nonzeros in the
column and row containing the element at the time it is selected
to be the next diagonal. Merit is the average of m
such quantities. It gives an indication of how much work was
required to preserve sparsity during the factorization.
- lenL
-
The number of nonzeros in L. On most machines, each nonzero
is represented by one eight-byte REAL and two two-byte
integer data types.
- lenU
-
The number of nonzeros in U. The storage required for each
nonzero is the same as for the nonzeros of L.
- Increase
-
The percentage increase in the number of nonzeros in L and U
relative to the number of nonzeros in B; i.e.,
100×(lenL + lenU − Elems)/Elems.
- m
-
is the number of rows in the problem. Note that m =
Ut+ Lt+ bp.
- Ut
-
is the number of triangular rows of B at the top of U.
- d1
-
is the number of columns remaining when the density of the
basis matrix being factorized reached 0.3.
- Lmax
-
The maximum subdiagonal element in the columns of L. This
will be no larger than the LU factor tolerance.
- Bmax
-
The maximum nonzero element in B.
- Umax
-
The maximum nonzero element in U, excluding elements of B
that remain in U unaltered. (For example, if a slack variable
is in the basis, the corresponding row of B will become a row
of U without alteration. Elements in such rows will not
contribute to Umax. If the basis is strictly triangular,
none of the elements of B will contribute, and Umax
will be zero.)
Ideally, Umax should not be substantially larger than
Bmax. If it is several orders of magnitude larger, it may
be advisable to reduce the LU factor tolerance to some value
nearer 1.0. (The default value is 10.0.)
Umax is not printed if BS is factorized.
- Umin
-
The smallest diagonal element of PUQ in absolute
magnitude.
- Growth
-
The ratio Umax / Bmax, which should not be too
large (see above).
As long as Lmax is not large (say 10.0 or less), the ratio
max{ Bmax, Umax } / Umin gives an
estimate of the condition number of B. If this number is
extremely large, the basis is nearly singular and some
numerical difficulties could conceivably occur. (However, an
effort is made to avoid near-singularity by using slacks to
replace columns of B that would have made Umin extremely
small. Messages are issued to this effect, and the modified
basis is refactored.)
- Lt
-
is the number of triangular columns of B at the beginning of
L.
- bp
-
is the size of the “bump” or block to be factorized
nontrivially after the triangular rows and columns have been
removed.
- d2
-
is the number of columns remaining when the density of the
basis matrix being factorized reached 0.6.
7.4.3 Crash statistics
When
Print Level≥ 20 and
Print file > 0, the
following CRASH statistics (< 120 characters) are produced on
the unit number specified by
Print file whenever
Start =
'Cold' (see §
7.3.2). They refer to the
number of columns selected by the CRASH procedure during each of
several passes through
A, whilst searching for a triangular basis
matrix.
-
Label
-
Description
- Slacks
-
is the number of slacks selected initially.
- Free cols
-
is the number of free columns in the basis.
- Preferred
-
is the number of “preferred” columns in the basis (i.e.,
hs(j) = 3 for some j ≤ n).
- Unit
-
is the number of unit columns in the basis.
- Double
-
is the number of double columns in the basis.
- Triangle
-
is the number of triangular columns in the basis.
- Pad
-
is the number of slacks used to pad the basis.
7.4.4 EXIT conditions
For each problem in the SPECS file, a message of the form
EXIT – message is printed to summarize the final result. Here
we describe each message and suggest possible courses of action.
A number is associated with each message below. It is the final value
assigned to the integer variable
inform.
| The following messages arise when the SPECS file is found to contain no further problems. |
Otherwise, the SPECS file may be empty, or cards containing the
keywords
Skip or
Endrun may imply that all problems should
be ignored (see §
7.3).
-1. ENDRUN
This message is printed at the end of a run if
SQOPT terminates of its own accord. Otherwise, the operating
system will have intervened for one of many possible reasons (excess
time, missing file, arithmetic error in the user routine, etc.).
| The following messages arise when optimization terminates gracefully. |
The final point seems
to be a unique solution of LCQP. This means that
x is
feasible (it satisfies the constraints to the accuracy
requested by the
Feasibility tolerance), the reduced gradient is
negligible, the reduced costs are optimal, and
R is nonsingular.
1. EXIT – the problem is infeasible
Feasibility is
measured with respect to the upper and lower bounds on the
variables. The message tells us that among all the points
satisfying the general constraints
Ax −
s = 0, there is apparently
no point that satisfies the bounds on
x and
s. Violations as
small as the
Feasibility tolerance are ignored, but at least one
component of
x or
s violates a bound by more than the tolerance.
Note: Although the objective function is the sum of infeasibilities
(when
nInf > 0), this sum will usually not have been
minimized when SQOPT recognizes the situation and exits.
There may exist other points that have a significantly lower sum of
infeasibilities.
2. EXIT – the problem is unbounded (or badly scaled)
For linear problems, unboundedness is detected by the simplex method
when a nonbasic variable can apparently be increased or decreased by
an arbitrary amount without causing a basic variable to violate a
bound. A message prior to the EXIT message will give the index of
the nonbasic variable. Consider adding an upper or lower bound to
the variable. Also, examine the constraints that have nonzeros in
the associated column, to see if they have been formulated as
intended.
Very rarely, the scaling of the problem could be so poor that
numerical error will give an erroneous indication of unboundedness.
Consider using the
Scale option.
3. EXIT – iteration limit exceeded
The
Iterations limit
was exceeded before the required solution could be found.
Check the iteration log to be sure that progress was being made. If
so, restart the run using a basis file that was saved (or
should have been saved!) at the end of the run.
4. EXIT – QP Hessian appears to be indefinite
The
problem appears to be nonconvex and cannot be solved using this
version of SQOPT. The matrix
H cannot be positive semidefinite,
i.e., there must exist a vector
y such that
yT Hy <0.
5. EXIT – the superbasics limit is too small: nnn
The problem appears to be more nonlinear than anticipated. The
current set of basic and superbasic variables have been optimized as
much as possible and a PRICE operation is necessary to continue,
but there are already
nnn superbasics (and no room for any
more).
In general, raise the
Superbasics limit s by a reasonable
amount, bearing in mind the storage needed for the reduced Hessian.
(The
Hessian dimension h will also increase to
s unless
specified otherwise, and the associated storage will be about 1/2
s2 words.) In extreme cases you may have to set
h<
s to conserve
storage, but beware that the rate of convergence will probably fall
off severely.
6. EXIT – weak solution found
The final point is a
weak minimizer. (The objective value is a global optimum,
but it may be achieved by an infinite set of points
x.)
This exit will occur when (i) the problem is feasible, (ii) the
reduced gradient is negligible, (iii) the Lagrange multipliers are
optimal, and (iv) the reduced Hessian is singular or there are some
very small multipliers. This exit cannot occur if
H is positive
definite (i.e.,
q(
x) is strictly convex).
10. EXIT – cannot satisfy the general constraints
An
LU
factorization of the basis has just been obtained and used to
recompute the basic variables
x B, given the present values of the
superbasic and nonbasic variables. A single step of “iterative
refinement" has also been applied to increase the accuracy of
x B.
However, a row check has revealed that the resulting solution does
not satisfy the current constraints
Ax −
s = 0 sufficiently well.
This probably means that the current basis is very ill-conditioned.
Request the
Scale option if there are any linear constraints and
variables.
For certain highly structured basis matrices (notably those with band
structure), a systematic growth may occur in the factor
U. Consult
the description of
Umax,
Umin and
Growth in
§
7.4.2, and set the
LU factor tolerance to
2.0 (or possibly even smaller, but not less than 1.0).
| If the following exits occur during the first basis
factorization, the basic variables x_Bwill have certain
default values that may not be particularly meaningful, and the
dual vector πwill be zero. |
An estimate of the additional storage required is given in messages
preceding the exit.
21. EXIT – error in basis package
A preceding message
will describe the error in more detail. One such message says that
the current basis has more than one element in row
i and column
j.
22. EXIT – singular basis after nnn factorization attempts
This exit is highly unlikely to occur. The first
factorization attempt will have found the basis to be structurally
or numerically singular. (Some diagonals of the triangular matrix
PUQ were respectively zero or smaller than a certain tolerance.)
The associated variables are replaced by slacks and the modified
basis is refactorized. The ensuing singularity must mean that the
problem is badly scaled, or the
LU factor tolerance is too high.
32. EXIT – system error. Wrong no. of basic variables: nnn
This exit should never happen. If it does, something is
seriously awry in the SQOPT source code.
| The following messages arise if additional storage is
needed to
allow optimization to begin. The problem is abandoned. |
7.5 Solution Output
At the end of a run, the final solution will be output to the
PRINT file. Some header information appears first to identify the
problem and the final state of the optimization procedure. A ROWS
section and a COLUMNS section then follow, giving one line of
information for each row and column. The format used is similar to
that seen in commercial systems, though there is no rigid industry
standard.
The ROWS section
The general constraints take the form
l ≤
Ax ≤
u. The
ith
constraint is therefore of the form
α ≤ aT x ≤ β.
Internally, the constraints take the form
Ax −
s = 0, where
s is the set of slack variables (which happen to satisfy the
bounds
l ≤
s ≤
u). For the
ith constraint it is the slack
variable
si that is directly available, and it is sometimes
convenient to refer to its state. To reduce clutter, a “ ”
is printed for any numerical value that is exactly zero.
-
Label
-
Description
- Number
-
The value n+i. This is the internal number used to refer to
the ith slack in the iteration log.
- Row
-
The name of the ith row.
- State
-
The state of the ith row relative to the bounds α
and β. The various states possible are as follows.
- State = LL
-
The row is at its lower limit, α.
- State = UL
-
The row is at its upper limit, β.
- State = EQ
-
The lower and upper limit are the same, α = β.
- State = BS
-
The constraint is not binding. si is basic.
- State = SBS
-
The constraint is not binding. si is superbasic.
-
-
A key is sometimes printed before the State to give some
additional information about the state of the slack variable.
- State key = A
-
Alternative optimum possible. The
slack is nonbasic, but its reduced gradient is
essentially zero. This means that if the slack were
allowed to start moving away from its bound, there
would be no change in the value of the objective
function. The values of the basic and superbasic
variables might change, giving a genuine
alternative solution. However, if there are any
degenerate variables (labelled D), the actual
change might prove to be zero, since one of them
could encounter a bound immediately. In either
case, the values of dual variables might also
change.
- State key = D
-
Degenerate. The slack is basic or
superbasic, but it is equal to (or very close to)
one of its bounds.
- State key = I
-
Infeasible. The slack is basic or
superbasic and it is currently violating one of its
bounds by more than the Feasibility tolerance.
- State key = N
-
Not precisely optimal. The slack is
nonbasic or superbasic. If the Optimality
tolerance were tightened by a factor of 10 (e.g.,
if it were reduced from 10−5 to 10−6), the
solution would not be declared optimal because the
reduced gradient for the slack would not be
considered negligible. (If a loose tolerance has
been used, or if the run was terminated before
optimality, this key might be helpful in deciding
whether or not to restart the run.)
Note: If Scale is specified, the tests for
assigning the A, D, I, N keys are
made on the scaled problem, since the keys are then
more likely to be correct.
- Activity
-
The row value; i.e., the value of aT x.
- Slack activity
-
The amount by which the row differs from its nearest bound.
(For free rows, it is taken to be minus the Activity.)
- Lower limit
-
α, the lower bound on the row.
- Upper limit
-
β, the upper bound on the row.
- Dual activity
-
The value of the dual variable πi, often called the
shadow price (or simplex multiplier) for the ith
constraint. The full vector π always satisfies BT π
= gB, where B is the current basis matrix and gB
contains the associated gradients for the current objective
function.
- I
-
The constraint number, i.
The COLUMNS section
Here we talk about the “column variables"
x. For convenience we
let the
jth component of
x be the variable
xj and assume that
it satisfies the bounds α ≤
xj ≤ β. A “ ”
is printed for any numerical value that is exactly zero.
-
Label
-
Description
- Number
-
The column number, j. This is the internal number used to refer
to xj in the iteration log.
- Column
-
The name of xj.
- State
-
The state of xj relative to the bounds α and
β. The various states possible are as follows.
- State = LL
-
xj is nonbasic at its lower limit, α.
- State = UL
-
xj is nonbasic at its upper limit, β.
- State = EQ
-
xj is nonbasic and fixed at the value α = β.
- State = FR
-
xj is nonbasic and currently zero, even though
it is free to take any value. (Its bounds are α =
−∞, β = +∞. Such variables are normally
basic.)
- State = BS
-
xj is basic.
- State = SBS
-
xj is superbasic.
A key is sometimes printed before the State to give some
additional information about the state of xj. The possible
keys are A, D, I and N. They have the same
meaning as described above (for the ROWS section of the
solution), but the words “the slack" should be replaced by
“xj".
- Activity
-
The value of the variable xj.
- Obj Gradient
-
gj, the jth component of the linear and quadratic
objective function q(x) + cT x. (We define gj=0 if
the current solution is infeasible.)
- Lower limit
-
α, the lower bound on xj.
- Upper limit
-
β, the upper bound on xj.
- Reduced gradnt
-
The reduced gradient dj = gj − πT aj, where aj is
the jth column of the constraint matrix (or the jth
column of the Jacobian at the start of the final major
iteration).
- M+J
-
The value m+j.
An example of the printed solution is given in
§
7.4. Infinite
Upper and
Lower limits are
output as the word
None. Other real values are output with
format
f16.5. The maximum record length is 111 characters,
including the first (carriage-control) character.
Note: If two problems are the same except that one minimizes
q(
x) and the other maximizes −
q(
x), their solutions will be the
same but the signs of the dual variables π
i and the reduced
gradients
dj will be reversed.
7.5.1 The SUMMARY file
If
Summary file f is specified certain brief information will
be output to file
f. For batch jobs a disk file should be used,
to retain a concise log of each run if desired. (A SUMMARY file
is more easily perused than the associated PRINT file).
A SUMMARY file (like the PRINT file) is not rewound after a
problem has been processed. It can therefore accumulate a log for
every problem in the SPECS file, if each specifies the same file.
The maximum record length is 72 characters, including a
carriage-control character in column 1.
The following information is included:
-
The Begin card from the SPECS file.
- The status of the solution after each basis factorization (whether
feasible; the objective value; the number of function calls so far).
- The same information every kth iteration, where k is the specified
Summary frequency (default k = 100).
- Warnings and error messages.
- The exit condition and a summary of the final solution.
Item 4 is preceded by a blank line, but item 5 is not.
All items are illustrated below, where we give the SUMMARY file
for the first problem in the example program (
Summary frequency =
1).
==============================
S Q O P T 5.3 (Oct 97)
==============================
Begin sqmain (Example program for sqopt)
Scale option 2, Partial price 1
----------------------------------------------------------------
Itn 0: Phase 1A -- making the linear equality rows feasible
Itn dj Step nInf SumInf Objective
0 0.0E+00 0.0E+00 1 8.868E+01 0.00000000E+00
1 0.0E+00 3.3E+01 0 0.000E+00 0.00000000E+00
Itn 1: Feasible linear equality rows
Itn 1: Phase 1B -- making all linear rows feasible
Itn dj Step nInf SumInf Objective Norm rg nS
1 0.0E+00 0.0E+00 2 5.317E+01 0.00000000E+00 3.4E+00 3
2 0.0E+00 0.0E+00 2 5.317E+01 0.00000000E+00 4.6E-01 2
3 0.0E+00 4.7E+02 1 2.896E+01 0.00000000E+00 4.8E-02 1
4 0.0E+00 9.2E+02 1 2.681E+01 0.00000000E+00 0.0E+00 0
This is problem sqmain. ncolH = 5
5 6.4E-02 6.5E+03 0 0.000E+00 -1.46750000E+06 0.0E+00 0
Itn 5: Feasible linear rows
6 -4.1E+03 2.1E-01 0 0.000E+00 -1.78368567E+06 0.0E+00 0
7 1.4E+03 1.0E+00 0 0.000E+00 -1.98453602E+06 1.4E-12 1
8 -6.3E+02 9.8E-01 0 0.000E+00 -2.04366386E+06 1.3E+01 1
9 0.0E+00 1.0E+00 0 0.000E+00 -2.04366504E+06 1.1E-12 1
EXIT -- optimal solution found
Problem name sqdat1..
No. of iterations 9 Objective value -2.0436650381E+06
No. of Hessian products 8 Linear objective 0.0000000000E+00
Quadratic objective -2.0436650381E+06
No. of superbasics 1 No. of basic nonlinears 2
No. of degenerate steps 1 Percentage 11.11
Norm of xs (scaled) 3.5E+03 Norm of pi (scaled) 8.9E+03
Norm of xs 1.6E+03 Norm of pi 1.1E+04
Max Prim inf(scaled) 0 0.0E+00 Max Dual inf(scaled) 6 2.0E-12
Max Primal infeas 0 0.0E+00 Max Dual infeas 3 9.6E-13
Solution printed on file 9
7.6 Algorithmic Details
SQOPT is based on an inertia-controlling method that maintains a
Cholesky factorization of the reduced Hessian (see below). The
method follows Gill and Murray [
14] and is described in
[
21]. Here we briefly summarize the main features of the
method. Where possible, explicit reference is made to items listed
in the printed output, and to the names of the relevant optional
parameters.
SQOPT's method has a
feasibility phase (also known as
phase 1), in which a feasible point is found by minimizing
the sum of infeasibilities, and an
optimality phase (or
phase 2), in which the quadratic objective is minimized
within the feasible region. The computations in both phases are
performed by the same subroutines, with the change of phase being
characterized by the objective changing from the sum of
infeasibilities (the printed quantity
sInf) to the quadratic
objective (the printed quantity
Objective).
In general, an iterative process is required to solve a quadratic
program. Given an iterate (
x,
s) in both the original variables
x and the slack variables
s, a new iterate (2.8
x,
s) is
defined by
where the
step length α is a non-negative scalar, and
p is called the
search direction. (For simplicity, we
shall consider a typical iteration and avoid reference to the index
of the iteration.) Once an iterate is feasible (i.e., satisfies the
constraints), all subsequent iterates remain feasible.
7.6.2 Definition of the working set
At each iterate (
x,
s), a
working set of constraints is
defined to be a linearly independent subset of the constraints that
are satisfied “exactly” (to within the value of the
Feasibility
tolerance). The working set is the current prediction of the
constraints that hold with equality at a solution of the LP or QP.
Let
mw denote the number of constraints in the working set
(including bounds), and let
W denote the associated
mw×(
n+
m)
working-set matrix consisting of the
mw
gradients of the working-set constraints.
The search direction is defined so that constraints in the working
set remain
unaltered for any value of the step length. It
follows that
p must satisfy the identity
W p = 0. This
characterization allows
p to be computed using any
n×
n Z
full-rank matrix
Z that spans the null space of
W. (Thus,
n Z
=
n −
mw and
W Z =0.) The null-space matrix
Z is defined from
a sparse
LU factorization of part of
W; see
(
44)–(
45) below). The direction
p will
satisfy
W p = 0 if
p =
Z p Z for any
n Z-vector
p Z.
The working set contains the constraints
Ax −
s = 0 and a subset
of the upper and lower bounds on the variables (
x,
s). Since the
gradient of a bound constraint
xj ≥
lj or
xj ≤
uj is a
vector of all zeros except for ± 1 in position
j, it follows
that the working-set matrix contains the rows of
( A −
I ) and
the unit rows associated with the upper and lower bounds in the
working set.
The working-set matrix
W can be represented in terms of a certain
column partition of the matrix
( A −
I ). As in
§
7.2 we partition the constraints
Ax −
s =
0 so that
BxB + SxS + NxN = 0,
where
B is a square non-singular basis and
xB,
xS and
xN
are the basic, superbasic and nonbasic variables respectively. The
nonbasic variables are equal to their upper or lower bounds at
(
x,
s), and the superbasic variables are independent variables that
are chosen to improve the value of the current objective. The number
of superbasic variables is
n S, which is printed as the quantity
nS. Given values of
x N and
x S, the basic variables
x B
are adjusted so that (
x,
s) satisfies
BxB +
SxS +
NxN = 0.
If
P is a permutation such that
( A −
I ) P =
( B S N ),
then the working-set matrix
W satisfies
where
I N is the identity matrix with the same number of columns
as
N.
The null-space matrix
Z is defined from a sparse
LU
factorization of part of
W. In particular,
Z is maintained in
“reduced-gradient" form, using the package LUSOL
[
2] to maintain sparse
LU factors of the basis matrix
B that alters as the working set
W changes. Given the
permutation
P, the null-space basis is given by
This matrix is used only as an operator, i.e., it is never computed
explicitly. Products of the form
Zv and
ZT g are obtained by
solving with
B or
BT. This choice of
Z implies that
n Z,
the number of “degrees of freedom” at (
x,
s), is the same as
n S, the number of superbasic variables.
Let
g Z and
H Z denote the
reduced gradient and
reduced Hessian:
g Z =
ZT g and
H Z =
ZT H Z,
(46)
where
g is the objective gradient at (
x,
s). Roughly
speaking,
g Z and
H Z describe the first and second derivatives
of an
n S-dimensional
unconstrained problem for the
calculation of
p Z. (The quantity
Cond Hz printed in the
summary-file output is a condition estimator of
H Z.)
At each iteration, an upper-triangular factor
R is available such
that
H Z =
RT R. Normally,
R is computed from
RT R =
ZT HZ
at the start of phase 2 and is then updated as the QP working set
changes. For efficiency the dimension of
R should not be
excessive (say,
n S ≤ 1000). This is guaranteed if the number
of nonlinear variables is “moderate”.
If the QP contains linear variables,
H is positive semi-definite
and
R may be singular with at least one zero diagonal. However,
an inertia-controlling active-set strategy is used to ensure that
only the last diagonal of
R can be zero. (See [
21]
for discussion of a similar strategy for indefinite quadratic
programming.)
If the initial
R is singular, enough variables are fixed at their
current value to give a nonsingular
R. This is equivalent to
including temporary bound constraints in the working set.
Thereafter,
R can become singular only when a constraint is
deleted from the working set (in which case no further constraints
are deleted until
R becomes nonsingular).
7.6.3 The main iteration
If the reduced gradient is zero, (
x,
s) is a constrained
stationary point on the working set. During phase 1, the reduced
gradient will usually be zero only at a vertex (although it may be
zero elsewhere in the presence of constraint dependencies). During
phase 2, a zero reduced gradient implies that
x minimizes the
quadratic objective when the constraints in the working set are
treated as equalities. At a constrained stationary point, Lagrange
multipliers λ are defined from the equations
WTλ =
g(
x). A Lagrange multiplier λ
j corresponding to an
inequality constraint in the working set is said to be
optimal if λ
j ≤ σ when the associated
constraint is at its
upper bound, or if λ
j ≥ −
σ when the associated constraint is at its
lower bound,
where σ depends on the
Optimality tolerance. If a
multiplier is non-optimal, the objective function (either the true
objective or the sum of infeasibilities) can be reduced by
continuing the minimization with the corresponding constraint
excluded from the working set (this step is sometimes referred to as
“deleting” a constraint from the working set). If optimal
multipliers occur during the feasibility phase but the sum of
infeasibilities is not zero, there is no feasible point.
The special form (
44) of the working set allows the
multiplier vector λ, the solution of
WTλ =
g, to be
written in terms of the vector
|
d = |

 |
|
|
|

 |
− ( A −I )Tπ
= |

 |
|
|
|

 |
,
(47) |
where π satisfies the equations
BTπ =
g B, and
g B
denotes the basic components of
g. The components of π are
the Lagrange multipliers λ
j associated with the equality
constraints
Ax −
s = 0. The vector
d N of nonbasic components
of
d consists of the Lagrange multipliers λ
j associated
with the upper and lower bound constraints in the working set. The
vector
d S of superbasic components of
d is the reduced gradient
g Z (
46). The vector
d B of basic components of
d is zero, by construction. (The Euclidean norm of
d S, and the
final values of
d S,
g and π are the quantities
norm rg,
Reduced Gradnt,
Obj Gradient and
Dual Activity in the
PRINT file output.)
If the reduced gradient is not zero, Lagrange multipliers need not
be computed and the search direction is given by
p =
Z Z p Z,
where
p Z is defined below. The step length is chosen to maintain
feasibility with respect to the satisfied constraints.
There are two possible choices for
p Z, depending on whether or
not
H Z is singular. If
H Z is nonsingular,
R is nonsingular
and
p Z is computed from the equations,
where
g Z is the reduced gradient at
x. In this case, (
x,
s) +
p is the minimizer of the objective function subject to the
working-set constraints being treated as equalities. If (
x,
s)+
p is
feasible, α is defined to be one. In this case, the reduced
gradient at (2.8
x,
s) will be zero, and Lagrange multipliers
are computed at the next iteration. Otherwise, α is set to
α
N, the step to the boundary of the “nearest” constraint
along
p. This constraint is added to the working set at the next
iteration.
If
H Z is singular, then
R must also be singular, and an
inertia-controlling strategy is used to ensure that only the last
diagonal element of
R is zero. (See [
21] for discussion
of a similar strategy for indefinite quadratic programming.) In
this case,
p Z satisfies
p ZT H Z p Z = 0 and
g ZT p Z ≤ 0,
which allows the objective function to be reduced by any step of the
form (
x,
s) + α
p, α > 0. The vector
p =
Zp Z is a
direction of unbounded descent for the QP in the sense that the QP
objective is linear and decreases without bound along
p. If no
finite step of the form (
x,
s) + α
p (α>0) reaches a
constraint not in the working set, the QP is unbounded and SQOPT
terminates at (
x,
s) and declares the problem to be unbounded.
Otherwise, α is defined as the maximum feasible step along
p and a constraint active at (
x,
s) + α
p is added to the
working set for the next iteration.
7.6.4 Miscellaneous
If the basis matrix is not chosen carefully, the condition of the
null-space matrix
Z (
45) could be arbitrarily high. To
guard against this, SQOPT implements a “basis repair" feature in
the following way. LUSOL is used to compute the rectangular
factorization
returning just the permutation
P that makes
PLPT unit lower
triangular. The pivot tolerance is set to require |
PLPT|
ij ≤
2, and the permutation is used to define
P in (
44).
It can be shown that
 Z
Z
is likely to be little more than 1.
Hence,
Z should be well-conditioned
regardless of the
condition of W.
This feature is applied at the beginning of the optimality phase if
a potential
B-
S ordering is known.
The EXPAND procedure (see Gill
et al. [
3]) is used to
reduce the possibility of cycling at a point where the active
constraints are nearly linearly dependent. Although there is no
absolute guarantee that cycling will not occur, the probability of
cycling is extremely small (see Hall and McKinnon [
22]). The
main feature of expand is that the feasibility tolerance is
increased at every iteration, perhaps at the expense of violating
the bounds on (
x,
s) by a simple amount.
Suppose that the value of
Feasibility tolerance is
δ. Over a period of
K iterations (where
K is the value of
the optional parameter
Expand frequency, the feasibility
tolerance used in SQOPT (i.e., the working feasibility tolerance)
increases from 1/2δ to δ in steps of
1/2δ/
K.
At certain stages, the following “resetting procedure” is used to
remove small constraint infeasibilities. First, all nonbasic
variables are moved exactly onto their bounds. A count is kept of
the number of non-trivial adjustments made. If the count is nonzero,
the basic variables are recomputed. Finally, the working feasibility
tolerance is reinitialized to 1/2δ.
If a problem requires more than
K iterations, the resetting
procedure is invoked and a new cycle of iterations is started. (The
decision to resume phase 1 or phase 2 is based on comparing any
constraint infeasibilities with δ.)
The resetting procedure is also invoked if when SQOPT reaches an
apparently optimal, infeasible, or unbounded solution, unless this
situation has already occurred twice. If any non-trivial adjustments
are made, iterations are continued.
The EXPAND procedure not only allows a positive step to be taken at
every iteration, but also provides a potential
choice of
constraint to be added to the working set. All constraints at a
distance α (α ≤ α
N) along
p from the current
point are then viewed as acceptable candidates for inclusion in the
working set. The constraint whose normal makes the biggest angle
with the search direction is added to the working set. This
strategy helps keep the basis matrix
B well-conditioned.
« Previous « Start » Next »












 Ax − s
Ax − s




















 π
π  ≥ −t or
dj /
≥ −t or
dj /  π
π  ≤ t
≤ t
 π
π  ≤ t for
superbasic variables.
≤ t for
superbasic variables. π
π  is a measure of the
size of the dual variables. It is included to make the
tests independent of a scale factor on the objective
function.
is a measure of the
size of the dual variables. It is included to make the
tests independent of a scale factor on the objective
function. π
π  actually used is defined by
actually used is defined by
 π
π = max{σ / √
= max{σ / √ Z
Z is likely to be little more than 1.
Hence, Z should be well-conditioned regardless of the
condition of W.
is likely to be little more than 1.
Hence, Z should be well-conditioned regardless of the
condition of W.