« Previous « Start » Next »
5 Algorithmic description
5.1 Overview
Classical methods for the solution of MINLP problems decompose the
problem by separating the nonlinear part from the integer part. This
approach is largely due to the existence of packaged software for
solving Nonlinear Programming (NLP) and Mixed Integer Linear
Programming problems.
In contrast, an integrated approach to solving MINLP problems is
considered here. This new algorithm is based on branch-and-bound,
but does not require the NLP problem at each node to be solved to
optimality. Instead, branching is allowed after each iteration of
the NLP solver. In this way, the nonlinear part of the MINLP problem
is solved whilst searching the tree. The nonlinear solver that is
considered in this manual is a Sequential Quadratic Programming
solver.
A numerical comparison of the new method with nonlinear
branch-and-bound is presented and a factor of up to 3
improvement over branch-and-bound is observed.
5.2 Introduction
This manual considers the solution of Mixed Integer Nonlinear Programming
(MINLP) problems. Problems of this type arise when some of the
variables are required to take integer values. Applications of MINLP
problems include the design of batch plants (e.g. [
17]
and [
22]), the synthesis of processes
(e.g. [
7]), the design of distillation sequences
(e.g. [
29]), the optimal positioning of products in a
multi-attribute space (e.g. [
7]), the minimization of
waste in paper cutting [
28] and the optimization
of core reload patterns for nuclear reactors [
1].
For a comprehensive survey of applications of MINLP applications see
Grossmann and Kravanja [
16].
MINLP problems can be modelled in the following form
| (P) |
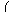


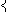


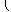 |
|
f(x,y) |
| subject to |
g(x,y) ≤ 0 |
| |
x  X, y X, y  Y integer, Y integer, |
|
|
where
y are the integer variables modelling for instance decisions
(
y 
{ 0 , 1 }), numbers of equipment (
y 
{ 0, 1, … ,
N })
or discrete sizes and
x are the continuous variables.
Classical methods for the solution of (
P) “decompose” the problem
by separating the nonlinear part from the integer part. This
approach is made possible by the existence of packaged
software for solving Nonlinear Programming (NLP) and Mixed Integer
Linear Programming (MILP) problems. The decomposition is even more
apparent in Outer Approximation ([
7] and
[
10]) and Benders Decomposition ([
15] and
[
13]) where an alternating sequence of MILP master
problems and NLP subproblems obtained by fixing the integer
variables is solved (see also the recent monograph of Floudas
[
14]). The recent branch-and-cut method for 0-1 convex
MINLP of Stubbs and Mehrotra [
27] also separates the
nonlinear
(lower bounding and cut generation) and integer part of the problem.
@percentBranch-and-bound [
6] can also be
viewed as a “decomposition” in which the tree-search (integer
part) is largely separated from solving the NLP problems at each
node (nonlinear part).
In contrast to these approaches, we considers an
integrated approach to MINLP problems. The algorithm developed here
is based on branch-and-bound, but instead of solving an NLP problem
at each node of the tree, the tree-search and the iterative solution
of the NLP are interlaced. Thus the nonlinear part of (
P) is
solved whilst searching the tree. The nonlinear solver that is
considered in this manual is a Sequential Quadratic Programming
(SQP) solver. SQP solves an NLP problem via a sequence of quadratic
programming (QP) problem approximations.
The basic idea underlying the new approach is to branch early –
possibly after a single QP iteration of the SQP solver. This idea
was first presented by Borchers and Mitchell [
4]. The
present algorithm improves on their idea in a number of ways:
-
In order to derive lower bounds needed in branch-and-bound
Borchers and Mitchell propose to evaluate the Lagrangian dual. This
is effectively an unconstrained nonlinear optimization problem. In
Section 5.4 it is shown that there is no need to compute a
lower bound if the linearizations in the SQP solver are interpreted as
cutting planes.
- In [4] two QP problems are solved before
branching. This restriction is due to the fact that a packaged
SQP solver is used. By using our own solver we are able to remove
this unnecessary restriction, widening the scope for early branching.
- A new heuristic for deciding when to branch early is introduced
which does not rely on a fixed parameter, but takes the
second order rate of convergence of the SQP solver into account
when deciding whether to branch or continue with the SQP iteration.
The ideas presented here have a similar motivation as a
recent algorithm by Quesada and Grossmann [
26]. Their
algorithm is related to outer approximation but avoids the
re-solution of related MILP master problems by interrupting the MILP
branch-and-bound solver each time an integer node is encountered. At
this node an NLP problem is solved (obtained by fixing all integer
variables) and new outer approximations are added to all problems on
the MILP branch-and-bound tree. Thus the MILP is updated and the
tree-search resumes. The difference to the approach considered here
is that Quesada and Grossmann still solve NLP problems at some
nodes, whereas the new solver presented here usually solves one
quadratic programming (QP) problem at each node.
The algorithmic description is organized as follows. Section
5.3 briefly
reviews the SQP method and branch-and-bound. In
Section
5.4 the new algorithm is developed for the
special case of convex MINLP problems. Section
5.4.4
introduces a heuristic for handling nonconvex MINLP problems.
Finally, Section
5.5 presents a comparison of the new
method with nonlinear branch-and-bound. These results are very
encouraging, often improving on branch-and-bound by a factor of up
to 3.
5.3 Background
5.3.1 Sequential Quadratic Programming
A popular iterative method for solving NLP problems is Sequential
Quadratic Programming (SQP). The basic form of SQP methods date back
to Wilson [
30] and were popularized by
Han [
19] and Powell [
25], see
Fletcher [
9, Chapter 12.4] and Conn, Gould and
Toint [
3] for a selection of other references. In
its basic form, SQP solves an NLP problem via a sequence of
quadratic programming (QP) approximations obtained by replacing the
nonlinear constraints by a linear first order Taylor series
approximation and the nonlinear objective by a second order Taylor
series approximation augmented by second order information from the
constraints. It can be shown under certain conditions that the SQP
method converges quadratically near a solution.
It is well known that the SQP method may fail to converge if it is
started far from a local solution. In order to induce convergence,
many popular methods use a
penalty function which is a
linear combination of the objective function
f and some measure of
the constraint violation. A related idea is an
augmented
Lagrangian function in which a weighted penalty term is added to
a Lagrangian function. A step in an SQP method is then accepted when
it produces a sufficient decrease in the penalty function.
Two frameworks exist which enforce sufficient decrease, namely
line-search in the direction of the QP solution or a trust-region
that limits the QP step that is computed (see e.g. [
9, Chapter
12.4] and references therein). In our implementation global
convergence is promoted through the use of a trust-region and the
new concept of a “filter” [
11] which accepts a trial
point whenever the objective or the constraint violation is improved
compared to all previous iterates. The size of the trust-region is
reduced if the step is rejected and increased if it is accepted.
5.3.2 Branch-and-bound
Branch-and-bound dates back to Land and Doig [
23]. The
first reference to nonlinear branch-and-bound can be found in
Dakin [
6]. It is most conveniently explained in terms of a
tree-search.
Initially, all integer restrictions are relaxed and the resulting NLP
relaxation is solved. If all integer variables take an integer value
at the solution then this solution also solves the MINLP. Usually,
some integer variables take a non-integer value. The algorithm then
selects one of those integer variables which take a non-integer
value, say
yi with value
yi, and branches on it. Branching generates two new NLP problems
by adding simple bounds
yi ≤ [
yi ] and
yi ≥ [
yi ] + 1 respectively to the NLP relaxation (where
[
a] is the largest integer not greater than
a).
One of the two new NLP problems is selected and solved next. If the
integer variables take non-integer values then branching is
repeated, thus generating a branch-and-bound tree whose nodes
correspond to NLP problems and where an edge indicates the addition
of a branching bound. If one of the following fathoming rules is
satisfied, then no branching is required, the corresponding node has
been fully explored (fathomed) and can be abandoned. The fathoming
rules are
-
FR1
- An infeasible node is detected. In this case the whole subtree
starting at this node is infeasible and the node has been
fathomed.
- FR2
- An integer feasible node is detected. This provides an upper
bound on the optimum of the MINLP; no branching is possible
and the node has been fathomed.
- FR3
- A lower bound on the NLP solution of a node is greater or equal
than the current upper bound. In this case the node is fathomed,
since this NLP solution provides a lower bound for all
problems in the corresponding sub-tree.
Once a node has been fathomed the algorithm backtracks to another
node which has not been fathomed until all nodes are fathomed.
Many heuristics exist for selecting a branching variable and for
choosing the next problem to be solved after a node has been
fathomed (see surveys by Gupta and Ravindran [
18] and
Volkovich et.al. [
24]).
Branch-and-bound can be inefficient in practice since it
requires the solution of one NLP problem per node which is usually
solved iteratively through a sequence of quadratic programming
problems. Moreover, a large number of NLP problems are solved which
have often no physical meaning if the integer variables do not take
integer values.
5.4 Integrating SQP and branch-and-bound
An alternative to nonlinear branch-and-bound for
convex MINLP
problems is due to Borchers and Mitchell [
4]. They observe that it
is not necessary to solve the NLP at each node to optimality before branching
and propose an
early branching rule, which
branches on an integer variable before the NLP has converged. Borchers and
Mitchell implement this approach and report encouraging numerical results
compared to Outer Approximation [
5]. In their implementation the
SQP solver is interrupted after two QP solves
(Ideally one would prefer to interrupt the SQP method after each QP
solve. Borchers and Mitchell use an SQP method from the NAG library
which does not allow this.)
and branching is done on an integer variable which is more than a given
tolerance away from integrality.
The drawback of the
early branching rule is that since the
NLP problems are
not solved to optimality, there is no
guarantee that the current value of
f(
x,
y) is a lower bound. As a
consequence, bounding (fathoming rule
FR3) is no longer
applicable. Borchers and Mitchell seek to overcome this difficulty
by evaluating the Lagrangian dual for a given set of multiplier
estimates, λ. The evaluation of the Lagrangian dual amounts
to solving
| |
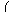

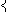

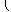 |
|
f(x,y) + λT g(x,y) |
| subject to |
x  X, y X, y  Y Y |
|
|
where the
Y ⊂
Y now also includes bounds that have
been added during the branching.
Note that this evaluation requires the solution of a bound constrained
nonlinear optimization problem. In order to diminish the costs of
these additional calculations, Borchers and Mitchell only evaluate
the dual every sixth QP solve.
Clearly, it would be desirable to avoid the solution of this problem and
at the same time obtain a lower bounding property at each QP solve.
In the remainder of this section it is shown how this can be
achieved by integrating the iterative NLP solver with the tree
search.
Throughout this section it is assumed that both
f and
g are
smooth,
convex functions. The nonconvex case is discussed in
Section
5.4.4 where a simple heuristic is proposed.
The ideas are first presented in the context of a basic SQP method
without globalization strategy. Next this basic algorithm is
modified to allow for the use of a line-search or a trust-region. It
is then shown how the early branching rule can take account of the
quadratic rate of convergence of the SQP method. Finally, a simple
heuristic for nonconvex MINLP problems is suggested.
5.4.1 The basic SQP algorithm
This section shows how the solution of the Lagrangian dual can be avoided
by interpreting the constraints of the QP approximation as
supporting hyperplanes. If
f and
g are convex, then the linear
approximations of the QP are outer approximations and this property
is exploited to replace the lower bounding.
Consider an NLP problem at a given node of the branch-and-bound tree,
| (P) |
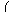


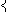


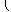 |
|
f(x,y) |
| subject to |
g(x,y) ≤ 0 |
| |
x  X, y X, y  Y , Y , |
|
|
where the integer restrictions have been relaxed and
Y
⊂
Y contains bounds that have been added by the branching.
Let
f denote the solution of (
P).
Applying the SQP method to (
P) results in solving a sequence
of QP problems of the form
| (QPk) |
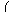


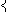


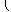 |
|
f(k) +  f(k)T d
+ f(k)T d
+ |
|
dT W(k) d |
|
| subject to |
g(k) +  g(k)T d ≤ 0 g(k)T d ≤ 0 |
| |
xk + dx  X, yk + dy X, yk + dy  Y . Y . |
|
|
where
f(k) =
f(
x(k),
y(k)) etc. and
W(k) 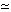
 2 L(k)
2 L(k)
=
 2 f(k)
2 f(k) +
Σλ
i  2 gi(k)
2 gi(k)
approximates the Hessian of the Lagrangian,
where λ
i is the Lagrange multiplier of
gi(
x,
y) ≤
0.
Unfortunately, the solution of (
QPk) does not underestimate
f,
even if all functions are assumed to be convex. This implies that
fathoming rule
FR3 cannot be used if early branching is
employed. However, it turns out that it is not necessary to compute
an underestimator explicitly. Instead, a mechanism is needed of
terminating the sequence of (
QPk) problems once such an
underestimator would become greater than the current upper bound,
U, of the branch-and-bound process. This can be achieved by adding
the
objective cut
f(k) +
 f(k)T d
f(k)T d ≤
U − є
to (
QPk), where є > 0 is the optimality tolerance of
branch-and-bound. Denote the new QP with this objective cut by
(
QPck).
| (QPck) |




 |
|
f(k) +  f(k)T d
+ f(k)T d
+ |
|
dT W(k) d |
|
| subject to |
g(k) +  g(k)T d ≤ 0 g(k)T d ≤ 0 |
| |
f(k) +  f(k)T d ≤ U − є f(k)T d ≤ U − є |
| |
xk + dx  X, yk + dy X, yk + dy  Y . Y . |
|
|
Note that (
QPck) is the QP that is generated by the SQP method when
applied to the following NLP problem
| |




 |
|
f(x,y) |
| subject to |
g(x,y) ≤ 0 |
| |
f(x,y) ≤ U − є |
| |
x  X, y X, y  Y , Y , |
|
|
where a nonlinear objective cut has been added to (
P). This
NLP problem is infeasible, if fathoming rule
FR3 holds at the
solution to (
P).
It is now possible to replace fathoming rule
FR3 applied to
(
P) by a test for feasibility of (
QPck) (replacing the
bounding in branch-and-bound). This results in the following lemma.
Lemma _under
Let f and g be smooth, convex functions. A sufficient condition
for fathoming rule FR3 applied to (P) to be satisfied
is that any QP problem (QPck) generated by the SQP method in
solving (P) is infeasible.
Proof: If (
QPck) is infeasible, then it follows
that there exists no step
d such that
|
|
f(k) +  f(k)T d f(k)T d |
≤ |
U − є |
(11) |
g(k) +  g(k)T d g(k)T d |
≤ |
0 .
|
(12) |
|
Since (
12) is an outer approximation of the nonlinear
constraints of (
P) and (
11) underestimates
f,
it follows that there exists no point (
x,
y)
 X
X
×
Y such that
f(x,y) ≤ U − є .
Thus any lower bound on
f at the present node has to be larger
than
U − є. Thus to within the tolerance є,
f ≥
U and
fathoming rule
FR3 holds.
q.e.d.
In practice, an SQP method would use a primal active set QP solver
which establishes feasibility first and then optimizes. Thus the
test of Lemma
1 comes at no extra cost. The basic
integrated SQP and branch-and-bound algorithm can now be stated.
Algorithm 1: Basic SQP and
branch-and-bound
Initialization: Place the continuous relaxation of
(
P) on the tree
and set
U = ∞.
| while (there are pending nodes in the tree) do |
|
Select an unexplored node. |
|
repeat (SQP iteration) |
|
|
1. Solve (QPck) for a step d(k) of the SQP method. |
|
|
2. if ((QPck) infeasible) then fathom
node, exit |
|
|
3. Set (x(k+1), y(k+1)) = (x(k), y(k))
+ (dx(k), dy(k)). |
|
|
4. if ((x(k+1), y(k+1)) NLP optimal)
then |
|
|
|
if (y(k+1) integral) then |
|
|
|
|
Update current best point by setting |
|
|
|
|
(x*,y*) = (x(k+1), y(k+1)),
f* = f(k+1) and U = f*. |
|
|
|
else |
|
|
|
|
Choose a non-integral yi(k+1) and branch. |
|
|
|
endif |
|
|
|
exit |
|
|
4. endif |
|
|
5. Compute the integrality gap
θ = maxi | yi(k+1)
− anint(yi(k+1)) |. |
|
|
6. if (θ > τ) then |
|
|
|
Choose a non-integral yi(k+1) and branch,
exit |
|
|
6. endif |
| end while
|
Here anint(
y) is the nearest integer to
y. Step 2 implements
the fathoming rule of Lemma
1 and Step 6 is the early
branching rule. In [
4] a value of τ = 0.1 is
suggested for the early branching rule and this value has also been
chosen here.
A convergence proof for this algorithm is given in the next section where
it is shown how the algorithm has to be modified if a line-search or
a trust-region is used to enforce global convergence for SQP. The
key idea in the convergence proof is that (as in nonlinear
branch-and-bound), the union of the child problems that are
generated by branching is equivalent to the parent problem. The
fact, that only a single QP has been solved in the parent problem
does not alter this equivalence. Finally, the new fathoming rule
implies
FR3 and hence, any node that has been fathomed by
Algorithm 1 can also be considered as having been fathomed by
nonlinear branch-and-bound. Thus convergence follows from the
convergence of branch-and-bound.
Algorithm 1 has two important advantages over the work in [
4].
Firstly, the lower bounding can be implemented at no additional cost
(compared to the need to solve the Lagrangian dual in
[
4]). Secondly, the lower bounding is available at
all nodes of the branch-and-bound tree
(rather than at every sixth node).
@percent Note that if no further branching is
possible at a node, then the algorithm resorts to normal SQP at that
node.
5.4.2 The globalized SQP algorithm
It is well known that the basic SQP method may fail to converge if
started far from a solution. In order to obtain a globally
convergent SQP method, descent in some merit function has to be
enforced. There are two concepts which enforce descent: a
line-search and a trust-region. This section describes how the basic
algorithm of the previous section has to be modified to accommodate
these global features.
The use of a line-search requires only to replace
d(k) by
α
(k) d(k), where α
(k) is the step-length chosen in
the line-search. Similarly a Levenberg-Marquardt approach would
require minimal change to the algorithm.
An alternative to using a line-search is to use a trust region.
Trust-region SQP methods usually possess stronger convergence
properties and this leads us to explore this approach. In this type
of approach the step that is computed in (
QPck) is restricted
to lie within a trust-region. Thus the QP that is being solved at
each iteration becomes
| (QPc,∞k) |



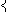



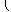 |
|
f(k) +  f(k)T d
+ f(k)T d
+ |
|
dT W(k) d |
|
| subject to |
g(k) +  g(k)T d ≤ 0 g(k)T d ≤ 0 |
| |
f(k) +  f(k)T d ≤ U − є f(k)T d ≤ U − є |
| |
 d d  ∞ ≤ ρk ∞ ≤ ρk |
| |
xk + dx  X, yk + dy X, yk + dy  Y Y |
|
|
where ρ
k is the trust-region radius which is adjusted
according to how well the quadratic model of (
QPc,∞k)
agrees with the true function (see [
9, Chapter 14.5] for
details).
The drawback of using a trust-region in the present context
is that the trust-region may cause (
QPc,∞k) to be
infeasible even though the problem without a trust-region (
QPck)
has a non-empty feasible region. Thus Lemma
1 is no
longer valid. However, if (
QPc,∞k) is infeasible and
the trust-region is inactive, then the argument of
Lemma
1 still holds and the node can be fathomed.
@percent Otherwise, the
feasibility
restoration phase has to be entered and this part of the SQP
method is briefly described next. The aim of the restoration phase
is to get closer to the feasible region by minimizing the violation
of the constraints in some norm, subject to the linear constraints
x  X
X,
y  Y
Y.
| (F) |
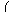

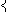

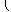 |
|
 h+(x,y) h+(x,y)  |
| subject to |
x  X, y X, y  Y, Y, |
|
|
where
and the operation
a+ = max( 0 ,
a ) is taken componentwise.
@percent In this phase, an SQP algorithm
is applied to minimize (
F). Methods for solving this problem
include Yuan [
31] for the
l∞ norm, El-Hallabi
and Tapia [
8] for the
l2 norm and Dennis, El-Alem
and Williamson [
21] for the
l1 norm. These
methods converge under mild assumptions similar to those needed for
the convergence of SQP methods. The details of the restoration phase
are beyond the scope of this manual and we concentrate instead on
the interaction between this phase and branch-and-bound. In the
remainder it will be assumed that this phase converges.
In order to obtain an efficient MINLP solver it is important to also
integrate the restoration phase with the tree-search. After each QP
in the restoration phase four possible outcomes arise.
-
(QPc,∞k) is feasible. In this case the solver exits the
restoration phase and resumes SQP and early branching.
- (QPc,∞k) is not feasible and a step d(k) is
computed for which the trust-region is inactive (
 d(k)
d(k)  < ρk).
This indicates that the current node can be fathomed by Lemma 1.
< ρk).
This indicates that the current node can be fathomed by Lemma 1.
- The feasibility restoration converges to a minimum of the constraint
violation (x*,y*) with
 h+(x*,y*)
h+(x*,y*)  > 0. This is taken
as an indication that (P) has no feasible point with an objective
that is lower than the current upper bound and the corresponding node can
be fathomed. Note that convergence of the feasibility SQP ensures that
the trust-region will be inactive at (x*,y*).
> 0. This is taken
as an indication that (P) has no feasible point with an objective
that is lower than the current upper bound and the corresponding node can
be fathomed. Note that convergence of the feasibility SQP ensures that
the trust-region will be inactive at (x*,y*).
- The feasibility restoration SQP continues if none of the above occur.
Thus the feasibility restoration can be terminated before convergence,
if 1 or 2 hold above. In the first case early branching resumes and
in the second case, the node can be fathomed.
The modifications required to make Algorithm 1 work for trust-region
SQP methods are given below.
Algorithm 2: Trust-region SQP and
branch-and-bound
Only steps 1. and 2. need to be changed to:
|
|
1'. Compute an acceptable step d(k) of the trust-region
SQP method. |
|
|
2'. if ((QPc,∞k) infeasible
and  d(k) d(k) ∞ < ρk) then ∞ < ρk) then |
|
|
|
fathom node exit |
|
|
2'.
elseif ((QPc,∞k) infeasible
and  d(k) d(k) ∞ = ρk) then ∞ = ρk) then |
|
|
|
Enter feasibility restoration phase: |
|
|
|
repeat (SQP iteration for feasibility restoration) |
|
|
|
|
(a) Compute a step of the feasibility restoration. |
|
|
|
|
(b) if ( d(k) d(k) ∞ < ρk)
then fathom node, exit ∞ < ρk)
then fathom node, exit |
|
|
|
|
(c) if ((QPc,∞k) feasible)
then return to normal SQP, exit |
|
|
|
|
(d) if (min g+(x,y) g+(x,y) > 0) then
fathom node, exit > 0) then
fathom node, exit |
|
|
2'. endif
|
The following theorem shows that Algorithm 2 converges under standard
assumptions (e.g.[
7] or [
10]).
Theorem _SQP_conv
If f and g are smooth and convex functions, if X and Y
are convex sets, if Y integer is finite and if the
underlying trust-region SQP method is globally convergent, then
Algorithm 2 terminates after visiting a finite number of nodes at
the solution (x*, y*) of (P).
Proof: The finiteness of
Y integer implies that
the branch-and-bound
tree is finite. Thus the algorithm must terminate after visiting a
finite number of nodes. Nodes are only fathomed if they are infeasible,
integer feasible or if the lower bounding of Lemma
1 holds.
Thus an optimal node must eventually be solved and convergence follows
from the convergence of the trust-region SQP method.
q.e.d.
5.4.3 Quadratic convergence and early branching
When implementing Algorithm 2 the following adverse
behaviour has been observed on some problems.
-
Some integer variables converge to a non-integral solution, namely
yi(k) → yi but θ
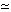 0.02 < τ,
i.e. the integrality gap remains bounded away from zero.
0.02 < τ,
i.e. the integrality gap remains bounded away from zero.
- The SQP solver converges at second order rate during this time and
θ ≫
 d(k)
d(k)  ∞ → 0.
∞ → 0.
In other words the early branching heuristic is not activated during
the second order convergence of the SQP method so that no early
branching takes
place in the final stages of the SQP solver (as τ = 0.1 is too large).
@percent One way to avoid this would be to reduce
τ, but this would simply repeat the problem at a smaller
threshold. Choosing τ to be of the order of the tolerance of
the SQP solver on the other hand would trigger early branching more
often which could duplicate the work to be done if integer variables
are converging to an integral solution.
These observations lead to a new early branching heuristic which takes
the quadratic rate of convergence of the SQP method into account.
Steps 5. and 6. of Algorithm 2 are replaced by
|
|
5'. Compute the integrality gap
θ = maxi | yi(k+1)
− anint(yi(k+1)) | |
|
|
5'. and the experimental order of convergence
p := ln( d(k) d(k)  ∞)
/ ln( ∞)
/ ln( d(k−1) d(k−1)  ∞). ∞). |
|
|
6'. if (θ > τ or (p > 1.5
and  d(k) d(k) ∞ < θ ))
then ∞ < θ ))
then |
|
|
|
Choose a non-integral yi(k+1) and branch,
exit |
|
|
6'. endif |
For a quadratically convergent method one expects that
p 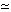
2
and once quadratic convergence sets in, that
 d(k+1)
d(k+1) ∞
∞
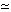
 d(k)
d(k) ∞p
∞p. Thus if
 d(k)
d(k) ∞
∞ < θ, one cannot expect to reduce the integrality
gap to zero in the remaining SQP iterations.
The new early branching rule resulted in a small but consistent reduction
in the number of QP problems solved (roughly a 5% reduction)
compared to the original heuristic.
5.4.4 Nonconvex MINLP problems
In practice many MINLP problems are nonconvex. In this case, the
underestimating property of Lemma
1 no longer holds, as
linearizations of nonconvex functions are not necessarily
underestimators. Thus it may be possible that a node is wrongly
fathomed on account of Lemma
1 and this could prevent
the algorithm from finding the global minimum.
A rigorous way of extending Algorithm 2 to classes of nonconvex MINLP
problems would be to replace the linearizations by linear
underestimators (e.g. Horst and Tuy [
20, Chapter VI]).
However, it is not clear what effect this would have on the
convergence properties of the SQP method. Instead the following
heuristic is proposed, which consists of replacing 2'. by 2”:
|
|
2”. if ((QPc,∞k) infeasible) then |
|
|
|
Enter feasibility restoration phase: |
|
|
|
repeat (SQP iteration) |
|
|
|
|
(a) Compute a step of the feasibility restoration. |
|
|
|
|
(c) if ((QPc,∞k) feasible)
then return to normal SQP, exit |
|
|
|
|
(d) if (min g+(x,y) g+(x,y) > 0) then
fathom node, exit > 0) then
fathom node, exit |
|
|
2”. endif
|
The main difference between 2'. and 2”. is that a node is no longer
fathomed if the QP problem is infeasible and the step lies strictly
inside the trust-region (
 d
d 
< ρ). Instead a feasibility
problem has to be solved to optimality (Step
(d) above) or
until a feasible QP problem is encountered (Step
(b) above).
This heuristic is motivated by the success of nonlinear
branch-and-bound in solving some nonconvex MINLP problems. It
ensures that a node is only fathomed if it
would have been fathomed by nonlinear branch-and-bound.
@percent Clearly, there is no guarantee that the
feasibility problem is solved to
global optimality if the
constraints or the objective are nonconvex.
5.5 Numerical Experience
Nonlinear branch-and-bound and Algorithm 2 have been implemented in
Fortran 77 using
filterSQP [
12] as the underlying
NLP solver. The implementation of Algorithm 2 uses a callback
routine that is invoked after each step of the SQP method. This
routine manages the branch-and-bound tree stored on a stack, decides
on when to branch and which problem to solve next. The use of this
routine has kept the necessary changes to
filterSQP to a
minimum.
|
| Header |
Description |
|
| problem |
The SIF name of the problem being solved. |
| n |
Total number of variables of the problem. |
| ni |
Number of integer variables of the problem. |
| m |
The total number of constraints (excl. simple bounds). |
| mn |
Number of nonlinear constraints. |
| k |
The dimension of the null–space at the solution. |
| # NLPs |
Number of NLP problems solved (branch-and-bound). |
| # nodes |
Number of nodes visited by Algorithm 2. |
| # QPs |
Total number of QP (and LP) problems solved. |
| # f-QPs |
Number of QPs in feasibility restoration. |
| CPU |
Seconds of CPU time needed for the solve. |
|
Table 3: Description of headers of the result tables
The test problems are from a wide range of backgrounds. Their
characteristics are displayed in Table
4. The SYNTHES*
problems are small process synthesis problems [
7].
OPTPRLOC is a problem arising from the optimal positioning of a
product in a multi-attribute space [
7]. BATCH is a
batch plant design problem that has been transformed to render it
convex [
22]. FEEDLOC is a problem arising from the
optimal sizing and feed tray location of a distillation column
[
29], TRIMLOSS is a trim loss optimization problem that
arises in the paper industry [
28] and TRIMLON4 is
an equivalent nonconvex formulation of the same problem. All
problems are input as SIF files [
2] plus an
additional file to identify the integer variables. The test-problems
are available at
http://www.mcs.dundee.ac.uk:8080/~
sleyffer/MINLP_TP/.
| problem |
n |
ni |
m |
mn |
Description |
| SYNTHES1 |
6 |
3 |
6 |
2 |
Process synthesis |
| SYNTHES2 |
11 |
5 |
14 |
3 |
Process synthesis |
| SYNTHES3 |
17 |
8 |
23 |
4 |
Process synthesis |
| OPTPRLOC |
30 |
25 |
30 |
25 |
Optimal product
location |
| BATCH |
49 |
24 |
73 |
1 |
Batch
plant design |
| FEEDLOC |
90 |
37 |
259 |
89 |
Distillation column
design (nonconvex) |
| TRIMLOSS |
142 |
122 |
75 |
4 |
Trimloss optimization |
| TRIMLON4 |
24 |
24 |
27 |
4 |
Trimloss
optimization
(nonconvex) |
Table 4: Problem characteristics of test problems
Table
3 lists a description of the headers of the result
tables. Table
4 list the problem characteristics. The
performance of branch-and-bound and Algorithm 2 is compared in
Table
5. All runs were performed on a SUN SPARC station 4
with 128 Mb memory, using the compiler options
-r8 -O and
SUN's
f77 Fortran compiler. In both algorithms a depth first
search with branching on the most fractional variable was
implemented.
| |
Branch-and-bound |
Algorithm 2 |
| problem |
# NLPs |
# QPs |
(# f-QPs) |
CPU |
# nodes |
# QPs |
(# f-QPs) |
CPU |
| SYNTHES1 |
5 |
18 |
(0) |
0.1 |
5 |
13 |
(0) |
0.1 |
| SYNTHES2 |
17 |
53 |
(0) |
0.4 |
17 |
40 |
(0) |
0.3 |
| SYNTHES3 |
25 |
80 |
(0) |
0.8 |
25 |
64 |
(3) |
0.8 |
| OPTPRLOC |
109 |
491 |
(119) |
8.5 |
112 |
232 |
(28) |
5.3 |
| BATCH |
143 |
371 |
(10) |
8.9 |
181 |
391 |
(11) |
14.8 |
| FEEDLOC |
47 |
340 |
(35) |
70.8 |
55 |
103 |
(4) |
29.0 |
| TRIMLOSS |
1336 |
3820 |
(160) |
254.3 |
944 |
1624 |
(1) |
90.3 |
| TRIMLON4 |
887 |
1775 |
(66) |
19.0 |
566 |
900 |
(112) |
13.3 |
Table 5: Results for branch-and-bound and Algorithm 2
Table
5 shows that branch-and-bound only requires about
2-6 QP solves per node that is solved making it a very efficient
solver. By comparison, Algorithm 2 often visits more nodes in the
branch-and-bound tree. That is not surprising, as the early
termination rule is based on a weaker lower bound than
FR2.
However, the overall number of QP problems that are being solved is
reduced by 20% – 80%. This results in a similar reduction
in terms of CPU time compared to branch-and-bound. For the largest
problem, Algorithm 2 is 3 times faster than nonlinear
branch-and-bound.
@percent
These results are roughly in line with what one might expect taking
into account that branch-and-bound solves between 3 and 5 QPs per
NLP node. They are somewhat better than the results in
[
5].
Even though problem TRIMLON4 is nonconvex, Algorithm 2 terminated with
the global minimum. For the nonconvex problem FEEDLOC, Algorithm 2
did not find an integer feasible point. This behaviour is due to the
fact that the linearization are
not outer approximations in
the nonconvex case and shows that the early termination rule does
not hold for nonconvex MINLP problems. Running Algorithm 2 in
nonconvex mode (see Section
5.4.4) produced the same
minimum as branch-and-bound. As one would expect, the performance of
Algorithm 2 in nonconvex mode is not as competitive as in convex
mode (see Table
6) but still competitive with
branch-and-bound. Better heuristics for nonconvex MINLP problems
remain an open problem.
| |
Branch-and-bound |
Algorithm 2 |
| problem |
# NLPs |
# QPs |
(# f-QPs) |
CPU |
# nodes |
# QPs |
(# f-QPs) |
CPU |
| FEEDLOC |
47 |
340 |
(35) |
70.8 |
65 |
159 |
(75) |
55.9 |
| TRIMLON4 |
887 |
1775 |
(66) |
19.0 |
984 |
1606 |
(259) |
21.9 |
Table 6: Results for Algorithm 2 in nonconvex mode
5.6 Conclusions
We have presented an algorithm for MINLP problems which interlaces the
iterative solution of each NLP node with the branch-and-bound tree search.
@percent The algorithm presented here can also be
interpreted as an improved lower bounding scheme for
branch-and-bound. An implementation of this idea gave a factor of
up to 3 improvement in terms of CPU time compared to
branch-and-bound.
« Previous « Start » Next »
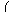


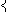


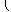
 { 0 , 1 }), numbers of equipment (y
{ 0 , 1 }), numbers of equipment (y  { 0, 1, … ,N })
or discrete sizes and x are the continuous variables.
{ 0, 1, … ,N })
or discrete sizes and x are the continuous variables.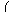

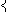

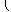
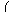


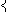


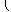
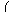


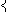


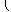
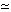
 2 L(k)
=
2 L(k)
=  2 f(k) + Σλi
2 f(k) + Σλi  2 gi(k)
2 gi(k)
 f(k)T d ≤ U − є
f(k)T d ≤ U − є
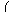


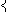


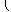
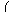


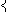


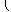
 X
× Y such that
X
× Y such that
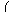



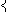



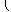
 X, y
X, y  Y.
Y.
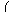

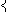

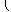




 d(k)
d(k)  < ρk).
This indicates that the current node can be fathomed by Lemma 1.
< ρk).
This indicates that the current node can be fathomed by Lemma 1.
 h+(x*,y*)
h+(x*,y*)  > 0. This is taken
as an indication that (P) has no feasible point with an objective
that is lower than the current upper bound and the corresponding node can
be fathomed. Note that convergence of the feasibility SQP ensures that
the trust-region will be inactive at (x*,y*).
> 0. This is taken
as an indication that (P) has no feasible point with an objective
that is lower than the current upper bound and the corresponding node can
be fathomed. Note that convergence of the feasibility SQP ensures that
the trust-region will be inactive at (x*,y*).
 d(k)
d(k) ∞ < ρk) then
∞ < ρk) then d(k)
d(k) ∞ = ρk) then
∞ = ρk) then d(k)
d(k) ∞ < ρk)
then fathom node, exit
∞ < ρk)
then fathom node, exit g+(x,y)
g+(x,y) > 0) then
fathom node, exit
> 0) then
fathom node, exit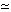 0.02 < τ,
i.e. the integrality gap remains bounded away from zero.
0.02 < τ,
i.e. the integrality gap remains bounded away from zero.
 d(k)
d(k)  ∞ → 0.
∞ → 0.
 d(k)
d(k)  ∞)
/ ln(
∞)
/ ln( d(k−1)
d(k−1)  ∞).
∞). d(k)
d(k) ∞ < θ ))
then
∞ < θ ))
then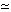 2
and once quadratic convergence sets in, that
2
and once quadratic convergence sets in, that  d(k+1)
d(k+1) ∞
∞
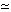
 d(k)
d(k) ∞p. Thus if
∞p. Thus if
 d(k)
d(k) ∞ < θ, one cannot expect to reduce the integrality
gap to zero in the remaining SQP iterations.
∞ < θ, one cannot expect to reduce the integrality
gap to zero in the remaining SQP iterations. g+(x,y)
g+(x,y) > 0) then
fathom node, exit
> 0) then
fathom node, exit d
d  < ρ). Instead a feasibility
problem has to be solved to optimality (Step (d) above) or
until a feasible QP problem is encountered (Step (b) above).
This heuristic is motivated by the success of nonlinear
branch-and-bound in solving some nonconvex MINLP problems. It
ensures that a node is only fathomed if it
would have been fathomed by nonlinear branch-and-bound.
< ρ). Instead a feasibility
problem has to be solved to optimality (Step (d) above) or
until a feasible QP problem is encountered (Step (b) above).
This heuristic is motivated by the success of nonlinear
branch-and-bound in solving some nonconvex MINLP problems. It
ensures that a node is only fathomed if it
would have been fathomed by nonlinear branch-and-bound.