« Previous « Start
8 Other special features
This section describes in more detail some of the most important
features of
Knitro and provides some guidance on which
features to use so that
Knitro runs most efficiently for the
problem at hand.
8.1 First derivative and gradient check options
The default version of
Knitro assumes that the user can
provide exact first derivatives to compute the objective function
gradient (in dense format) and constraint gradients (in sparse
form). It is
highly recommended that the user provide at
least exact first derivatives if at all possible, since using first
derivative approximations may seriously degrade the performance of
the code and the likelihood of converging to a solution. However, if
this is not possible or desirable the following first derivative
approximation options may be used.
Forward finite-differences
This option uses a forward finite-difference approximation of the
objective and constraint gradients. The cost of computing this
approximation is
n function evaluations where
n is the number of
variables. This option can be invoked by choosing
GRADOPT=2.
Centered finite-differences
This option uses a centered finite-difference approximation of the
objective and constraint gradients. The cost of computing this
approximation is 2
n function evaluations where
n is the number
of variables. This option can be invoked by choosing
GRADOPT=3. The centered finite-difference approximation may
often be more accurate than the forward finite-difference
approximation. However, it is more expensive since it requires twice
as many function evaluations to compute.
Gradient Checks
If the user is supplying a routine for computing exact gradients,
but would like to compare these gradients with finite-difference
gradient approximations as an error check this can easily be done in
Knitro. To perform a gradient check with
forward
finite-differences set
GRADOPT=4, and to perform a gradient
check with
centered finite-differences set
GRADOPT=5.
8.2 Second derivative options
The default version of
Knitro assumes that the user can
provide exact second derivatives to compute the Hessian of the
Lagrangian function. If the user is able to do so and the cost of
computing the second derivatives is not overly expensive, it is
highly recommended to provide exact second derivatives. However,
Knitro also offers other options which are described in detail
below.
(Dense) Quasi-Newton BFGS
The quasi-Newton BFGS option uses gradient information to compute a
symmetric,
positive-definite approximation to the Hessian
matrix. Typically this method requires more iterations to converge
than the exact Hessian version. However, since it is only computing
gradients rather than Hessians, this approach may be more efficient
in some cases. This option stores a
dense quasi-Newton
Hessian approximation so it is only recommended for small to medium
problems (
n < 1000). The quasi-Newton BFGS option can be chosen by
setting options value
HESSOPT=2.
(Dense) Quasi-Newton SR1
As with the BFGS approach, the quasi-Newton SR1 approach builds an
approximate Hessian using gradient information. However, unlike the
BFGS approximation, the SR1 Hessian approximation is not restricted
to be positive-definite. Therefore the quasi-Newton SR1
approximation may be a better approach, compared to the BFGS method,
if there is a lot of negative curvature in the problem since it may
be able to maintain a better approximation to the true Hessian in
this case. The quasi-Newton SR1 approximation maintains a
dense Hessian approximation and so is only recommended for
small to medium problems (
n < 1000). The quasi-Newton SR1 option
can be chosen by setting options value
HESSOPT=3.
Finite-difference Hessian-vector product option
If the problem is large and gradient evaluations are not the
dominate cost, then
Knitro can internally compute
Hessian-vector products using finite-differences. Each
Hessian-vector product in this case requires one additional gradient
evaluation. This option can be chosen by setting options value
HESSOPT=4. This option is generally only recommended if the
exact gradients are provided.
NOTE: This option may not be used when
ALG=1.
Exact Hessian-vector products
In some cases the user may have a large, dense Hessian which makes
it impractical to store or work with the Hessian directly, but the
user may be able to provide a routine for evaluating exact
Hessian-vector products.
Knitro provides the user with this
option. This option can be chosen by setting options value
HESSOPT=5.
NOTE: This option may not be used when
ALG=1.
Limited-memory Quasi-Newton BFGS
The limited-memory quasi-Newton BFGS option is similar to the dense
quasi-Newton BFGS option described above. However, it is better
suited for large-scale problems since, instead of storing a dense
Hessian approximation, it only stores a limited number of gradient
vectors used to approximate the Hessian. The number of gradient
vectors used to approximate the Hessian is controlled by user option
LMSIZE which must be between 1 and 100 (10 is the default). A larger
value of LMSIZE may result in a more accurate, but also more
expensive, Hessian approximation. A smaller value may give a less
accurate, but faster, Hessian approximation. When using the limited
memory BFGS approach it is recommended to experiment with different
values of this parameter. In general, the limited-memory BFGS option
requires more iterations to converge than the dense quasi- Newton
BFGS approach, but will be much more efficient on large-scale
problems. This option can be chosen by setting options value
HESSOPT=6.
8.3 Feasible version
Knitro offers the user the option of forcing intermediate
iterates to stay feasible with respect to the
inequality
constraints (it does not enforce feasibility with respect to the
equality constraints however). Given an initial point
which is
sufficiently feasible with respect to all
inequality constraints and selecting
FEASIBLE = 1, forces
all the iterates to strictly satisfy the inequality constraints
throughout the solution process. For the feasible mode to become
active the iterate
x must satisfy
cl +
tol ≤
c(
x) ≤
cu −
tol
(16)
for
all inequality constraints (i.e., for
cl cu).
The tolerance
tol>0 by which an iterate must be strictly feasible
for entering the feasible mode is determined by the parameter
FEASMODETOL which is
1.0e-4 by default. If the initial point
does not satisfy
16 then the default infeasible version
of
Knitro will run until it obtains a point which is
sufficiently feasible with respect to all the inequality
constraints. At this point it will switch to the feasible version
of
Knitro and all subsequent iterates will be forced to
satisfy the inequality constraints.
NOTE: This option may only be used when
ALG=1 or 2.
8.4 Honor Bounds
By default
Knitro does not enforce that the simple bounds on
the variables
1 are satisfied throughout the optimization
process. Rather, satisfaction of these bounds is only enforced at
the solution. In some applications, however, the user may want to
enforce that the initial point and all intermediate iterates satisfy
the bounds
xL ≤
x ≤
xU. This can be enforced by setting
HONORBNDS=1.
8.5 Crossover
Interior point (or barrier) methods are a powerful tool for solving
large-scale optimization problems. However, one drawback of these
methods, in contrast to active-set methods, is that they do not
always provide a clear picture of which constraints are active at
the solution and in general they return a less exact solution and
less exact sensitivity information. For this reason,
Knitro
offers a
crossover feature in which the interior-point
method switches to the active-set method at the interior-point
solution estimate, in order to try to “clean up” the solution and
provide more exact sensitivity and active-set information.
The crossover procedure is controlled by the
MAXCROSSIT
user option. If this parameter is greater than 0, then
Knitro
will attempt to perform
MAXCROSSIT active-set crossover
iterations after the interior-point method has finished, to see if
it can provide a more exact solution. This can be viewed as a form
of post-processing. If
MAXCROSSIT<=0, then no crossover
iterations are attempted. By default, no crossover iterations are
performed.
The crossover procedure will not always succeed in obtaining a more
exact solution compared with the interior-point solution. If
crossover is unable to improve the solution within
MAXCROSSIT crossover iterations, then it will restore the
interior-point solution estimate and terminate. If
PriLevOpt>1,
Knitro will print a message indicating
that it was unable to improve the solution. For example, if
MAXCROSSIT=3, and the crossover procedure did not succeed
within 3 iterations, the message will read:
Crossover mode unable to improve solution within 3 iterations.
In this case, you may want to increase the value of
MAXCROSSIT and try again. If it appears that the crossover
procedure will not succeed, no matter how many iterations are tried,
then a message of the form
Crossover mode unable to improve solution.
will be printed.
The extra cost of performing crossover is problem dependent. In
most small or medium scale problems, the crossover cost should be a
small fraction of the total solve cost. In these cases it may be
worth using the crossover procedure to obtain a more exact solution.
On some large scale or difficult degenerate problems, however, the
cost of performing crossover may be significant. It is recommended
to experiment with this option to see whether the improvement in the
exactness of the solution is worth the additional cost.
8.6 Multi-start
Nonlinear optimization problems are often nonconvex due to the
objective function, constraint functions, or both. When this is
true, there may be many points that satisfy the local optimality
conditions described in section
5. Default
Knitro behavior is to return the first locally optimal point found.
Knitro offers a simple
multi-start feature that
searches for a better optimal point by restarting
Knitro from
different initial points. The feature is enabled by setting
MULTISTART=1.
The multi-start procedure generates new start points by randomly
selecting
x components that satisfy the variable bounds.
The number of start points to try is specified with the option
MSMAXSOLVES.
Knitro finds a local optimum from each
start point using the same problem definition and user options. The
solution returned is the local optimum with the best objective
function value. If
PriLevOpt is greater than 3, then
Knitro prints details of each local optimum.
The multi-start option is convenient for conducting a simple search
for a better solution point. It can also save execution and memory
overhead by internally managing the solve process from successive
start points.
In most cases the user would like to obtain the
global
optimum; that is, the local optimum with the very best objective
function value.
Knitro cannot guarantee that mult-start will
find the global optimum. The probability of finding a better point
improves if more start points are tried, but so does the execution
time. Search time can be improved if the variable bounds are made as
tight as possible. Minimally,
all variables need to be given
finite upper and lower bounds.
8.7 Solving Systems of Nonlinear Equations
Knitro is quite effective at solving systems of nonlinear
equations. To solve a square system of nonlinear equations using
Knitro one should specify the nonlinear equations using
clsAssign in TOMLAB. The same applies for least squares
problems described below.
8.8 Solving Least Squares Problems
There are two ways of using
Knitro for solving problems in which the objective
function is a sum of squares of the form
If the value of the objective function at the solution is not close to zero
(the large residual case), the least squares structure of
f can be ignored and the
problem can be solved as any other optimization problem. Any of the
Knitro
options can be used.
On the other hand, if the optimal
objective function value is expected to be small (small residual case) then
Knitro can implement the Gauss-Newton or Levenberg-Marquardt methods which
only require first derivatives of the residual functions,
rj(
x),
and yet converge rapidly.
To do so, the user need only define the Hessian
of
f to be
 2 f
2 f(
x) =
J(
x)
TJ(
x),
where
The actual Hessian is given by
 2 f(x) = J(x)T J(x) + 2 f(x) = J(x)T J(x) + |
|
rj(x)  2 rj(x); 2 rj(x);
|
the Gauss-Newton and Levenberg-Marquardt approaches consist of
ignoring the last term in the Hessian.
Knitro will behave like a Gauss-Newton method by setting
ALG=1, and will be very similar to the classical
Levenberg-Marquardt method when
ALG=2.
8.9 Mathematical programs with equilibrium constraints (MPECs)
A mathematical program with equilibrium (or complementarity)
constraints (also know as an MPEC or MPCC) is an optimization
problem which contains a particular type of constraint referred to
as a complementarity constraint. A complementarity constraint is a
constraint which enforces that two variables are
complementary
to each other, i.e., the variables
x1 and
x2 are complementary
if the following conditions hold
x1 ×
x2 = 0,
x1 ≥ 0,
x2 ≥ 0.
(17)
The condition above, is sometimes expressed more compactly as
0 ≤ x1 ⊥ x2 ≥ 0.
One could also have more generally, that a particular constraint is
complementary to another constraint or a constraint is complementary
to a variable. However, by adding slack variables, a
complementarity constraint can always be expressed as two variables
complementary to each other, and
Knitro requires that you
express complementarity constraints in this form. For example, if
you have two constraints
c1(
x) and
c2(
x) which are
complementary
c1(x) × c2(x) = 0, c1(x) ≥ 0, c2(x) ≥ 0,
you can re-write this as two equality constraints and two
complementary variables,
s1 and
s2 as follows:
|
|
| s1 |
= |
c1(x) |
(18) |
| s2 |
= |
c2(x) |
(19) |
| s1 × s2 |
= |
0, s1 ≥ 0, s2 ≥ 0.
|
(20) |
|
Intuitively, a complementarity constraint is a way to model a
constraint which is combinatorial in nature since, for example, the
conditions in
17 imply that either
x1 or
x2 must
be 0 (both may be 0 as well). Without special care, these type of
constraints may cause problems for nonlinear optimization solvers
because problems which contain these types of constraints fail to
satisfy constraint qualifications which are often assumed in the
theory and design of algorithms for nonlinear optimization. For
this, reason we provide a special interface in
Knitro for
specifying complementarity constraints. In this way,
Knitro
can recognize these constraints and apply some special care to them
internally.
Assume we want to solve the following MPEC with
Knitro.
|
|
|
|
f(x) = (x0 − 5)2 + (2 x1 + 1)2 |
(21) |
| subject to |
|
c0(x) = 2(x1 − 1) − 1.5 x0 + x2 − 0.5
x3 + x4 = 0 |
(22) |
| |
|
c1(x) = 3 x0 − x1 − 3 ≥ 0 |
(23) |
| |
|
c2(x) = −x0 + 0.5 x1 + 4 ≥ 0 |
(24) |
| |
|
c3(x) = −x0 − x1 + 7 ≥ 0 |
(25) |
| |
|
xi ≥ 0, i=0..4 |
(26) |
| |
|
c1(x) x2 = 0 |
(27) |
| |
|
c2(x) x3 = 0 |
(28) |
| |
|
c3(x) x4 = 0 .
|
(29) |
|
It is easy to see that the last 3 constraints (along with the
corresponding non-negativity conditions) represent complementarity
constraints. Expressing this in compact notation, we have:
|
|
|
|
f(x) = (x0 − 5)2 + (2 x1 + 1)2 |
(30) |
| subject to |
|
c0(x) = 0 |
(31) |
| |
|
0 ≤ c1(x) ⊥ x2 ≥ 0 |
(32) |
| |
|
0 ≤ c2(x) ⊥ x3 ≥ 0 |
(33) |
| |
|
0 ≤ c3(x) ⊥ x4 ≥ 0 |
(34) |
| |
|
x0 ≥ 0, x1 ≥ 0 .
|
(35) |
|
Since
Knitro requires that complementarity constraints be
written as two variables complementary to each other, we must
introduce slack variables
x5,
x6,
x7 and re-write problem
8.9 as
|
|
|
|
f(x) = (x0 − 5)2 + (2 x1 + 1)2 |
(36) |
| subject to |
|
c0(x) = 2(x1 − 1) − 1.5 x0 + x2 − 0.5
x3 + x4 = 0 |
(37) |
| |
|
c1(x) = 3 x0 − x1 − 3 − x5 = 0 |
(38) |
| |
|
c2(x) = −x0 + 0.5 x1 + 4 − x6 = 0 |
(39) |
| |
|
c3(x) = −x0 − x1 + 7 − x7 = 0 |
(40) |
| |
|
xi ≥ 0, i=0..7 |
(41) |
| |
|
x2 ⊥ x5 |
(42) |
| |
|
x3 ⊥ x6 |
(43) |
| |
|
x4 ⊥ x7 .
|
(44) |
|
In order to create MPEC problems with TOMLAB the
lcpAssign ,
qpcAssign and
mcpAssign routines should be used. The
additional slack variables are automatically handled when using
these.
8.10 Global optimization
Knitro is designed for finding locally optimal solutions of
continuous optimization problems. A local solution is a feasible
point at which the objective function value at that point is as good
or better than at any “nearby” feasible point. A globally optimal
solution is one which gives the best (i.e., lowest if minimizing)
value of the objective function out of all feasible points. If the
problem is
convex all locally optimal solutions are also
globally optimal solutions. The ability to guarantee convergence to
the global solution on large-scale
nonconvex problems is a
nearly impossible task on most problems unless the problem has some
special structure or the person modeling the problem has some
special knowledge about the geometry of the problem. Even finding
local solutions to large-scale, nonlinear, nonconvex problems is
quite challenging.
Although
Knitro is unable to guarantee convergence to global
solutions it does provide a
multi-start heuristic which
attempts to find multiple local solutions in the hopes of locating
the global solution. See section
8.6 for information on
trying to find the globally optimal solution using the
Knitro
multi-start feature.
« Previous « Start
 2 f(x) = J(x)TJ(x),
2 f(x) = J(x)TJ(x),
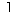
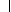
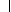
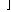
 2 f(x) = J(x)T J(x) +
2 f(x) = J(x)T J(x) +  2 rj(x);
2 rj(x);