« Previous « Start » Next »
14 Linear Semi-Definite w LMI
In
sdp_prob there is 1 linear semi-definite programming test problem with linear matrix inequalities
with 3 variables.
In order to define this problem and solve it execute the following in Matlab:
Prob = probInit('spd_prob',1);
Result = tomRun('',Prob);
An example of a problem of this class,
(that is also found in the TOMLAB quickguide) is glbQG:
|
|
|
f(x) = cTx |
| |
|
| s/t |
xL |
≤ |
x |
≤ |
xU |
| |
bL |
≤ |
Ax |
≤ |
bU |
| |
| Q0i + |
|
n Qkixk 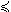 0, i=1,…,m. 0, i=1,…,m. |
|
|
(16) |
where
c,
x,
xL,
xU  Rn
Rn,
A  Rml
× n
Rml
× n,
bL,
bU  Rml
Rml and
Qki are
symmetric matrices of similar dimensions in each constraint
i.
If there are several LMI constraints, each may have it's own
dimension.
The following file is required to define a problem of this category in TOMLAB.
File: tomlab/quickguide/sdpQG.m
The following file illustrates how to define and solve a problem
of this category in TOMLAB.
This problem appears to be infeasible.
% sdpQG is a small example problem for defining and solving
% semi definite programming problems with linear matrix
% inequalities using the TOMLAB format.
Name = 'sdp.ps example 2';
% Objective function
c = [1 2 3]';
% Two linear constraints
A = [ 0 0 1 ; 5 6 0 ];
b_L = [-Inf; -Inf];
b_U = [ 3 ; -3 ];
x_L = -1000*ones(3,1);
x_U = 1000*ones(3,1);
% Two linear matrix inequality constraints. It is OK to give only
% the upper triangular part.
SDP = [];
% First constraint
SDP(1).Q{1} = [2 -1 0 ; 0 2 0 ; 0 0 2];
SDP(1).Q{2} = [2 0 -1 ; 0 2 0 ; 0 0 2];
SDP(1).Qidx = [1; 3];
% Second constraint
SDP(2).Q{1} = diag( [0 1] );
SDP(2).Q{2} = diag( [1 -1] );
SDP(2).Q{3} = diag( [3 -3] );
SDP(2).Qidx = [0; 1; 2];
x_0 = [];
Prob = sdpAssign(c, SDP, A, b_L, b_U, x_L, x_U, x_0, Name);
Result = tomRun('pensdp', Prob, 1);
« Previous « Start » Next »
 Rn, A
Rn, A  Rml
× n, bL,bU
Rml
× n, bL,bU  Rml and Qki are
symmetric matrices of similar dimensions in each constraint i.
If there are several LMI constraints, each may have it's own
dimension.
Rml and Qki are
symmetric matrices of similar dimensions in each constraint i.
If there are several LMI constraints, each may have it's own
dimension.