« Previous « Start » Next »
32 Drug Displacement Problem
ITERATIVE DYNAMIC PROGRAMMING, REIN LUUS
12.4.3 Example 3: The desired level of two drugs, warfarin and phenylbutazone, must be reached in a patients bloodstream in minimum time.
CHAPMAN & HALL/CRC Monographs and Surveys in Pure and Applied Mathematics
32.1 Problem Formulation
Find u over t in [0; t ] to minimize
subject to:
| = g1*(g4*(0.02−x1)+46.4*x1*(u−2*x2)) |
| = g1*(g3*(u−2*x2)+46.4*(0.02−x1)) |
x1 is the concentration of warfarin, and x2 of phenylbutazone. The initial and final condition are:
Reference: [25]
32.2 Problem setup
toms t
toms t_f
p = tomPhase('p', t, 0, t_f, 50);
setPhase(p);
tomStates x1 x2
tomControls u
% Initial guess
x0 = {t_f == 300
icollocate({
x1 == 0.02; x2 == 2*t/t_f})
collocate(u == 8-8*t/t_f)};
% Box constraints
cbox = { 1 <= t_f <= 500
0 <= collocate(u) <= 8};
% Boundary constraints
cbnd = {initial({x1 == 0.02; x2 == 0})
final({x1 == 0.02; x2 == 2})};
% General variables
g2 = 1+0.2*(x1+x2);
g3 = g2.^2+232+46.4*x2;
g4 = g2.^2+232+46.4*x1;
g1 = g2.^2./(g3.*g4-2152.96*x1.*x2);
% ODEs and path constraints
ceq = collocate({
dot(x1) == g1.*(g4.*(0.02-x1)+46.4*x1.*(u-2*x2))
dot(x2) == g1.*(g3.*(u-2*x2)+46.4*(0.02-x1))});
32.3 Solve the problem
options = struct;
options.name = 'Drug Displacement';
% Objective is first parameter
solution = ezsolve(t_f, {cbox, cbnd, ceq}, x0, options);
t = subs(collocate(t),solution);
u = subs(collocate(u),solution);
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Drug Displacement f_k 221.333418113505130000
sum(|constr|) 0.000000061271395437
f(x_k) + sum(|constr|) 221.333418174776540000
f(x_0) 300.000000000000000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 14 ConJacEv 14 Iter 10 MinorIter 256
CPU time: 0.140625 sec. Elapsed time: 0.140000 sec.
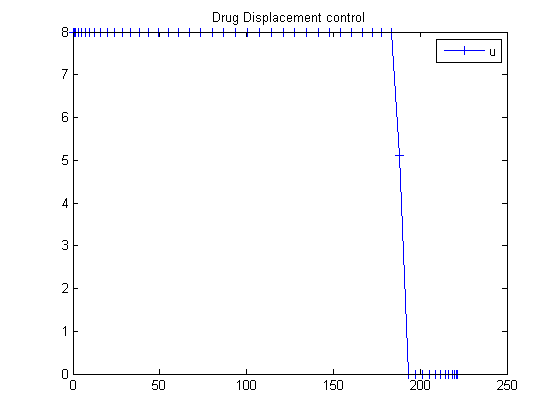
32.4 Plot result
figure(1)
plot(t,u,'+-');
legend('u');
title('Drug Displacement control');
« Previous « Start » Next »