« Previous « Start » Next »
94 Time-optimal Trajectories for Robot Manipulators
Users Guide for dyn.Opt, Example 2
Dissanayake, M., Goh, C. J., & Phan-Thien, N., Time-optimal Trajectories for Robot Manipulators, Robotica, Vol. 9, pp. 131-138, 1991.
94.1 Problem Formulation
Find u over t in [0; t_F ] to minimize
subject to:
| H11 = Eye1 + Eye2 + m1*el12 + m2*(L12+el22+2.0*L1*el2*cos(x2)); |
| H12 = Eye2 + m2*el22 + m2*L1*el2*cos(x2); |
| = delta*(2.0*h*H22*x3*x4+h*H22*x42 + h*H12*x32+H22*u1−H12*u2); |
| = delta*(−2.0*h*H12*x3*x4−h*H11*x32− h*H12*x42+H11*u2−H12*u1); |
Reference: [16]
94.2 Problem setup
toms t
toms t_f
tfopt = 7;
x1opt = 1*t/t_f;
x2opt = -2+1*t/t_f;
x3opt = 2;
x4opt = 4;
u1opt = 10-20*t/t_f;
u2opt = -10+20*t/t_f;
94.3 Solve the problem, using a successively larger number collocation points
for n=[30 60]
p = tomPhase('p', t, 0, t_f, n);
setPhase(p);
tomStates x1 x2 x3 x4
tomControls u1 u2
% Initial guess
x0 = {t_f == tfopt
icollocate({
x1 == x1opt
x2 == x2opt
x3 == x3opt
x4 == x4opt})
collocate({
u1 == u1opt
u2 == u2opt})};
% Box constraints
cbox = {
0.1 <= t_f <= 50
-10 <= collocate(u1) <= 10
-10 <= collocate(u2) <= 10};
% Boundary constraints
cbnd = {initial({x1 == 0; x2 == -2
x3 == 0; x4 == 0})
final({x1 == 1; x2 == -1
x3 == 0; x4 == 0})};
% ODEs and path constraints
L_1 = 0.4; L_2 = 0.4;
m_1 = 0.5; m_2 = 0.5;
Eye_1 = 0.1; Eye_2 = 0.1;
el_1 = 0.2; el_2 = 0.2;
H_11 = Eye_1 + Eye_2 + m_1*el_1^2+ ...
m_2*(L_1^2+el_2^2+2.0*L_1*el_2*cos(x2));
H_12 = Eye_2 + m_2*el_2^2 + m_2*L_1*el_2*cos(x2);
H_22 = Eye_2 + m_2*el_2^2;
h = m_2*L_1*el_2*sin(x2);
delta = 1.0./(H_11.*H_22-H_12.^2);
ceq = collocate({
dot(x1) == x3
dot(x2) == x4
dot(x3) == delta.*(2.0*h.*H_22.*x3.*x4 ...
+h.*H_22.*x4.^2+h.*H_12.*x3.^2+H_22.*u1-H_12.*u2)
dot(x4) == delta.*(-2.0*h.*H_12.*x3.*x4 ...
-h.*H_11.*x3.^2-h.*H_12.*x4.^2+H_11.*u2-H_12.*u1)});
% Objective
objective = t_f;
94.4 Solve the problem
options = struct;
options.name = 'Robot Manipulators';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
% Optimal x, y, and speed, to use as starting guess
% in the next iteration
tfopt = subs(final(t), solution);
x1opt = subs(x1, solution);
x2opt = subs(x2, solution);
x3opt = subs(x3, solution);
x4opt = subs(x4, solution);
u1opt = subs(u1, solution);
u2opt = subs(u2, solution);
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Robot Manipulators f_k 0.391698237386178260
sum(|constr|) 0.000063099634834817
f(x_k) + sum(|constr|) 0.391761337021013070
f(x_0) 7.000000000000000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 68 ConJacEv 68 Iter 26 MinorIter 437
CPU time: 0.421875 sec. Elapsed time: 0.437000 sec.
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Robot Manipulators f_k 0.391820155673056890
sum(|constr|) 0.000000000017635038
f(x_k) + sum(|constr|) 0.391820155690691950
f(x_0) 0.391698237386178260
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 16 ConJacEv 16 Iter 12 MinorIter 440
CPU time: 0.515625 sec. Elapsed time: 0.547000 sec.
end
t = subs(collocate(t),solution);
x1 = subs(collocate(x1opt),solution);
x2 = subs(collocate(x2opt),solution);
x3 = subs(collocate(x3opt),solution);
x4 = subs(collocate(x4opt),solution);
u1 = subs(collocate(u1opt),solution);
u2 = subs(collocate(u2opt),solution);
94.5 Plot result
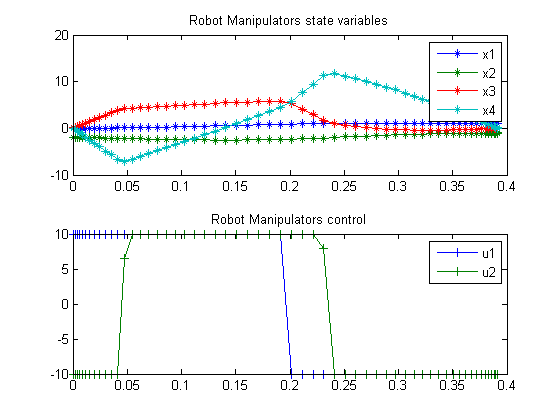
subplot(2,1,1)
plot(t,x1,'*-',t,x2,'*-',t,x3,'*-',t,x4,'*-');
legend('x1','x2','x3','x4');
title('Robot Manipulators state variables');
subplot(2,1,2)
plot(t,u1,'+-',t,u2,'+-');
legend('u1','u2');
title('Robot Manipulators control');
« Previous « Start » Next »