« Previous « Start » Next »
48 Hang Glider Control
Benchmarking Optimization Software with COPS Elizabeth D. Dolan and Jorge J. More ARGONNE NATIONAL LABORATORY
48.1 Problem Formulation
Find u(t) over t in [0; t_F ] to maximize
subject to:
| = | | *(−L*sin(neta)−D*cos(neta)) |
| = | | *(L*cos(neta)−D*sin(neta)) − g |
| D = | | *(c0+c1**cL2)*rho*S*v2 |
cL is the control variable.
Reference: [14]
48.2 Problem setup
toms t
toms t_f
for n=[10 80]
p = tomPhase('p', t, 0, t_f, n, [], 'cheb');
setPhase(p);
tomStates x dx y dy
tomControls cL
% Initial guess
% Note: The guess for t_f must appear in the list before
% expression involving t.
if n == 10
x0 = {t_f == 105
icollocate({
dx == 13.23; x == dx*t
dy == -1.288; y == 1000+dy*t
})
collocate(cL==1.4)};
else
x0 = {t_f == tf_opt
icollocate({
dx == dx_opt; x == x_opt
dy == dy_opt; y == y_opt
})
collocate(cL == cL_opt)};
end
% Box constraints
cbox = {
0.1 <= t_f <= 200
0 <= icollocate(x)
0 <= icollocate(dx)
0 <= collocate(cL) <= 1.4};
% Boundary constraints
cbnd = {initial({x == 0; dx == 13.23
y == 1000; dy == -1.288})
final({dx == 13.23; y == 900; dy == -1.288})};
% Various constants and expressions
m = 100; g = 9.81;
uc = 2.5; r0 = 100;
c0 = 0.034; c1 = 0.069662;
S = 14; rho = 1.13;
r = (x/r0-2.5).^2;
u = uc*(1-r).*exp(-r);
w = dy-u;
v = sqrt(dx.^2+w.^2);
sinneta = w./v;
cosneta = dx./v;
D = 1/2*(c0+c1*cL.^2).*rho.*S.*v.^2;
L = 1/2*cL.*rho.*S.*v.^2;
% ODEs and path constraints
ceq = collocate({
dot(x) == dx
dot(dx) == 1/m*(-L.*sinneta-D.*cosneta)
dot(y) == dy
dot(dy) == 1/m*(L.*cosneta-D.*sinneta)-g
dx.^2+w.^2 >= 0.01});
% Objective
objective = -final(x);
48.3 Solve the problem
options = struct;
options.name = 'Hang Glider';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Hang Glider f_k -1281.388593956430400000
sum(|constr|) 0.000000000082304738
f(x_k) + sum(|constr|) -1281.388593956348100000
f(x_0) -1389.149999999999600000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 55 ConJacEv 55 Iter 37 MinorIter 191
CPU time: 0.250000 sec. Elapsed time: 0.250000 sec.
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Hang Glider f_k -1305.253702077266800000
sum(|constr|) 0.000000045646790482
f(x_k) + sum(|constr|) -1305.253702031619900000
f(x_0) -1281.388593956420700000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 80 ConJacEv 80 Iter 67 MinorIter 801
CPU time: 4.468750 sec. Elapsed time: 4.547000 sec.
48.4 Extract optimal states and controls from solution
x_opt = subs(x,solution);
dx_opt = subs(dx,solution);
y_opt = subs(y,solution);
dy_opt = subs(dy,solution);
cL_opt = subs(cL,solution);
tf_opt = subs(t_f,solution);
end
48.5 Plot result
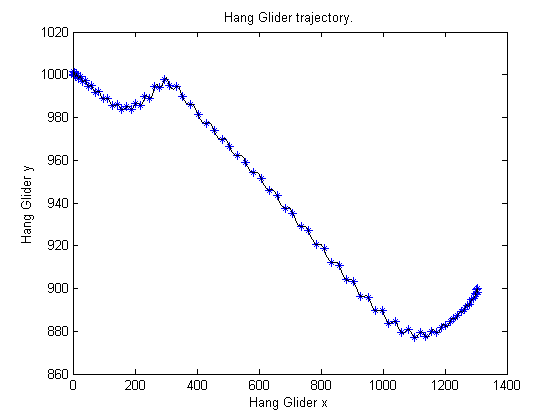
figure(1)
ezplot(x,y);
xlabel('Hang Glider x');
ylabel('Hang Glider y');
title('Hang Glider trajectory.');
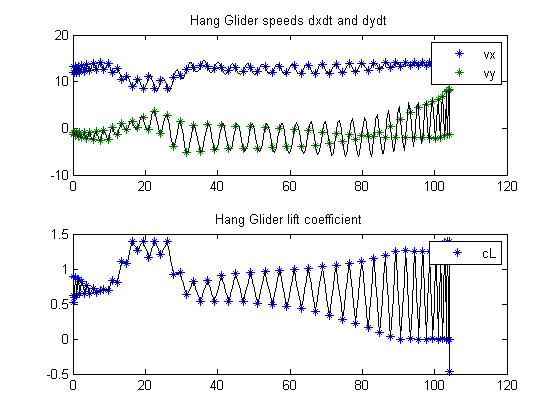
figure(2)
subplot(2,1,1)
ezplot([dx; dy]);
legend('vx','vy');
title('Hang Glider speeds dxdt and dydt');
subplot(2,1,2)
ezplot(cL);
legend('cL');
title('Hang Glider lift coefficient');
« Previous « Start » Next »