« Previous « Start » Next »
3 Problem Types and Solver Routines
Section
3.1 defines all problem types in TOMLAB . Each
problem definition is accompanied by brief suggestions on suitable
solvers. This is followed in Section
3.2 by a complete
list of the available solver routines in TOMLAB and the various
available extensions, such as /SOL and /CGO.
3.1 Problem Types Defined in TOMLAB
The
unconstrained optimization (
uc) problem is defined as
where
x,
xL,
xU  Rn
Rn and
f(
x)
 R
R. For unbounded variables, the corresponding elements of
xL,
xU may be set to ± ∞.
Recommended solvers:
TOMLAB /KNITRO and TOMLAB /SNOPT.
The TOMLAB Base Module routine
ucSolve includes several of
the most popular search step methods for unconstrained
optimization. Bound constraints are treated as described in Gill
et. al. [
31]. The search step methods for
unconstrained optimization included in
ucSolve are: the
Newton method, the quasi-Newton BFGS and DFP method, the
Fletcher-Reeves and Polak-Ribiere conjugate-gradient method, and
the Fletcher conjugate descent method. The quasi-Newton methods
may either update the inverse Hessian (standard) or the Hessian
itself. The Newton method and the quasi-Newton methods updating
the Hessian use a subspace minimization technique to handle rank
problems, see Lindström [
56]. The quasi-Newton
algorithms also use safe guarding techniques to avoid rank problem
in the updated matrix.
Another TOMLAB Base Module solver suitable for unconstrained
problems is the structural trust region algorithm
sTrustr ,
combined with an initial trust region radius algorithm. The code
is based on the algorithms in [
15] and [
70],
and treats partially separable functions. Safeguarded BFGS or DFP
are used for the quasi-Newton update, if the analytical Hessian is
not used. The set of constrained nonlinear solvers could also be
used for unconstrained problems.
The
quadratic programming (
qp) problem is defined as
|
|
|
|
| |
|
| s/t |
| xL |
≤ |
x |
≤ |
xU, |
| bL |
≤ |
A x |
≤ |
bU |
|
|
(2) |
where
c,
x,
xL,
xU  Rn
Rn,
F  Rn × n
Rn × n,
A  Rm1 × n
Rm1 × n, and
bL,
bU  Rm1
Rm1.
Recommended solvers:
TOMLAB /KNITRO, TOMLAB /SNOPT and
TOMLAB /MINLP.
A positive semidefinite
F-matrix gives a convex QP, otherwise
the problem is nonconvex. Nonconvex quadratic programs are solved
with a standard active-set method [
57], implemented in
the TOM routine
qpSolve .
qpSolve explicitly treats
both inequality and equality constraints, as well as lower and
upper bounds on the variables (simple bounds). It converges to a
local minimum for indefinite quadratic programs.
In TOMLAB
MINOS in the general or the QP-version
(
QP-MINOS ), or the dense QP solver
QPOPT may be
used. In the TOMLAB /SOL extension the
SQOPT solver is
suitable for both dense and large, sparse convex QP and
SNOPT works fine for dense or sparse nonconvex QP.
For very large-scale problems, an interior point solver is
recommended, such as TOMLAB /KNITRO or TOMLAB /BARNLP.
TOMLAB /CPLEX, TOMLAB /Xpress and TOMLAB /XA should always be
considered for large-scale QP problems.
The
constrained nonlinear optimization problem (
con)
is defined as
|
|
|
f(x) |
| |
|
| s/t |
| xL |
≤ |
x |
≤ |
xU, |
| bL |
≤ |
A x |
≤ |
bU |
| cL |
≤ |
c(x) |
≤ |
cU |
|
|
(3) |
where
x,
xL,
xU  Rn
Rn,
f(
x)
 R
R,
A
 Rm1 × n
Rm1 × n,
bL,
bU  Rm1
Rm1
and
cL,
c(
x),
cU  Rm2
Rm2.
Recommended solvers:
TOMLAB /SNOPT, TOMLAB /NPSOL and
TOMLAB /KNITRO.
For general constrained nonlinear optimization a sequential
quadratic programming (SQP) method by Schittkowski [
72]
is implemented in the TOMLAB Base Module solver
conSolve .
conSolve also includes an implementation of the Han-Powell
SQP method. There are also a TOMLAB Base Module routine
nlpSolve implementing the Filter SQP by Fletcher and
Leyffer presented in [
24].
Another constrained solver in TOMLAB is the structural trust region
algorithm
sTrustr , described above. Currently,
sTrustr only solves problems where the feasible region,
defined by the constraints, is convex. TOMLAB /MINOS solves
constrained nonlinear programs. The TOMLAB /SOL extension gives an
additional set of general solvers for dense or sparse problems.
sTrustr ,
pdco and
pdsco in TOMLAB Base Module handle
nonlinear problems with
linear constraints only.
There are many other options for large-scale nonlinear
optimization to consider in TOMLAB . TOMLAB /CONOPT, TOMLAB /BARNLP,
TOMLAB /MINLP, TOMLAB /NLPQL and TOMLAB /SPRNLP.
The
box-bounded global optimization (
glb) problem is defined as
where
x,
xL,
xU  Rn
Rn,
f(
x)
 R
R, i.e.
problems of the form (
1) that have finite simple bounds on
all variables.
Recommended solvers:
TOMLAB /LGO and TOMLAB /CGO with
TOMLAB /SOL.
The TOM solver
glbSolve implements the DIRECT
algorithm [
16], which is a modification of the standard
Lipschitzian approach that eliminates the need to specify a
Lipschitz constant. In
glbSolve no derivative information
is used. For global optimization problems with expensive function
evaluations the TOMLAB /CGO routine
ego implements the
Efficient Global Optimization (EGO) algorithm
[
18]. The idea of the EGO algorithm is to first
fit a response surface to data collected by evaluating the
objective function at a few points. Then, EGO balances
between finding the minimum of the surface and improving the
approximation by sampling where the prediction error may be high.
The
global mixed-integer nonlinear programming (
glc)
problem is defined as
|
|
|
f(x) |
| |
|
| s/t |
| −∞ < |
xL |
≤ |
x |
≤ |
xU |
< ∞ |
| |
bL |
≤ |
A x |
≤ |
bU |
|
| |
cL |
≤ |
c(x) |
≤ |
cU, |
xj  N N  j j  I, I, |
|
|
(5) |
where
x,
xL,
xU  Rn
Rn,
f(
x)
 R
R,
A
 Rm1 × n
Rm1 × n,
bL,
bU  Rm1
Rm1
and
cL,
c(
x),
cU  Rm2
Rm2.
The variables
x  I
I, the index subset of 1,...,
n, are restricted to be
integers.
Recommended solvers:
TOMLAB /OQNLP.
The TOMLAB Base Module solver
glcSolve implements an
extended version of the DIRECT algorithm [
55],
that handles problems with both nonlinear and integer constraints.
The
linear programming (
lp) problem is defined as
|
|
|
f(x) = cT x |
| |
|
| s/t |
| xL |
≤ |
x |
≤ |
xU, |
| bL |
≤ |
A x |
≤ |
bU |
|
|
(6) |
where
c,
x,
xL,
xU  Rn
Rn,
A  Rm1 × n
Rm1 × n, and
bL,
bU  Rm1
Rm1.
Recommended solvers:
TOMLAB /CPLEX, TOMLAB /Xpress and
TOMLAB /XA.
The TOMLAB Base Module solver
lpSimplex implements a simplex
algorithm for
lp problems.
When a dual feasible point is known in (
6) it is
efficient to use the dual simplex algorithm implemented in the
TOMLAB Base Module solver
DualSolve . In TOMLAB /MINOS the LP
interface to
MINOS , called
LP-MINOS is efficient for
solving large, sparse LP problems. Dense problems are solved by
LPOPT . The TOMLAB /SOL extension gives the additional
possibility of using
SQOPT to solve large, sparse LP.
The recommended solvers normally outperforms all other solvers.
The
mixed-integer programming problem
(
mip)
is defined as
|
|
|
f(x) = cT x |
| |
|
| s/t |
| xL |
≤ |
x |
≤ |
xU, |
| bL |
≤ |
A x |
≤ |
bU,
xj  N N  j j  I I |
|
|
(7) |
where
c,
x,
xL,
xU  Rn
Rn,
A  Rm1
× n
Rm1
× n, and
bL,
bU  Rm1
Rm1. The variables
x
 I
I, the index subset of 1,...,
n are restricted to be
integers. Equality constraints are defined by setting the lower
bound equal to the upper bound, i.e. for constraint
i:
bL(
i)
=
bU(
i).
Recommended solvers:
TOMLAB /CPLEX, TOMLAB /Xpress and
TOMLAB /XA.
Mixed-integer programs can be solved using the TOMLAB Base Module
routine
mipSolve that implements a standard branch-and-bound
algorithm, see Nemhauser and Wolsey [
61, chap. 8]. When
dual feasible solutions are available, mipSolve is using the TOMLAB
dual simplex solver DualSolve to solve subproblems, which is
significantly faster than using an ordinary linear programming
solver, like the TOMLAB lpSimplex.
mipSolve also implements
user defined priorities for variable selection, and different tree
search strategies. For 0/1 - knapsack problems a round-down primal
heuristic is included. Another TOMLAB Base Module solver is the
cutting plane routine
cutplane , using Gomory cuts. It is
recommended to use
mipSolve with the LP version of
MINOS with warm starts for the subproblems, giving great
speed improvement. The TOMLAB /Xpress extension gives access to the
state-of-the-art LP, QP, MILP and MIQP solver Xpress-MP. For many
MIP problems, it is necessary to use such a powerful solver, if the
solution should be obtained in any reasonable time frame. TOMLAB
/CPLEX is equally powerful as TOMLAB /Xpress and also includes a
network solver.
The
linear least squares (
lls) problem
is defined as
|
|
|
|
| |
|
| s/t |
| xL |
≤ |
x |
≤ |
xU, |
| bL |
≤ |
A x |
≤ |
bU |
|
|
(8) |
where
x,
xL,
xU  Rn
Rn,
d  RM
RM,
C  RM × n
RM × n,
A  Rm1 × n
Rm1 × n,
bL,
bU  Rm1
Rm1
and
cL,
c(
x),
cU  Rm2
Rm2.
Recommended solvers:
TOMLAB /LSSOL.
Tlsqr solves unconstrained sparse
lls problems.
lsei solves the general dense problems.
Tnnls is a
fast and robust replacement for the Matlab nnls. The general
least squares solver
clsSolve may also be used. In the
TOMLAB /NPSOL or TOMLAB /SOL extension the
LSSOL solver is
suitable for dense linear least squares problems.
The
constrained nonlinear least squares (
cls) problem
is defined as
|
|
|
|
| |
|
| s/t |
| xL |
≤ |
x |
≤ |
xU, |
| bL |
≤ |
A x |
≤ |
bU |
| cL |
≤ |
c(x) |
≤ |
cU |
|
|
(9) |
where
x,
xL,
xU  Rn
Rn,
r(
x)
 RM
RM,
A  Rm1 × n
Rm1 × n,
bL,
bU  Rm1
Rm1
and
cL,
c(
x),
cU  Rm2
Rm2.
Recommended solvers:
TOMLAB /NLSSOL.
The TOMLAB Base Module nonlinear least squares solver
clsSolve treats problems with bound constraints in a
similar way as the routine
ucSolve . This strategy is
combined with an active-set strategy to handle linear equality and
inequality constraints [
7].
clsSolve includes four optimization methods for nonlinear
least squares problems: the Gauss-Newton method, the
Al-Baali-Fletcher [
2] and the Fletcher-Xu
[
22] hybrid method, and the Huschens TSSM method
[
53]. If rank problems occur, the solver uses subspace
minimization. The line search algorithm used is the same as for
unconstrained problems.
Another fast and robust solver is
NLSSOL , available in the
TOMLAB /NPSOL or the TOMLAB /SOL extension toolbox.
One important utility routine is the TOMLAB Base Module line search
algorithm
LineSearch , used by the solvers
conSolve ,
clsSolve and
ucSolve . It implements a modified
version of an algorithm by Fletcher [
23, chap. 2]. The
line search algorithm uses quadratic and cubic interpolation, see
Section
12.9.
Another TOMLAB Base Module routine,
preSolve , is running a
presolve analysis on a system of linear equalities, linear
inequalities and simple bounds. An algorithm by Gondzio
[
39], somewhat modified, is implemented in
preSolve . See [
7] for a more detailed
presentation.
The
linear semi-definite programming problem with linear matrix inequalities
(
sdp) is defined as
|
|
|
f(x) = cTx |
| |
|
| s/t |
xL |
≤ |
x |
≤ |
xU |
| |
bL |
≤ |
Ax |
≤ |
bU |
| |
| Q0i + |
|
n Qkixk 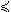 0, i=1,…,m. 0, i=1,…,m. |
|
|
(10) |
where
c,
x,
xL,
xU  Rn
Rn,
A  Rml
× n
Rml
× n,
bL,
bU  Rml
Rml and
Qki are
symmetric matrices of similar dimensions in each constraint
i.
If there are several LMI constraints, each may have it's own dimension.
Recommended solvers:
TOMLAB /PENSDP and TOMLAB /PENBMI.
The
linear semi-definite programming problem with bilinear
matrix inequalities (
bmi) is defined similarly to but with
the matrix inequality
|
|
Q0i + |
|
n Qkixk + |
|
n |
|
n xkxlKkli 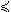 0 (11) 0 (11) |
The MEX solvers
pensdp and
penbmi treat
sdp and
bmi problems, respectively. These are available in the
TOMLAB /PENSDP and TOMLAB /PENBMI toolboxes.
The MEX-file solver
pensdp available in the TOMLAB /PENSDP toolbox
implements a penalty method aimed at large-scale dense and sparse
sdp problems. The interface to the solver allows for data
input in the sparse SDPA input format as well as a TOMLAB specific
format corresponding to.
The MEX-file solver
penbmi available in the TOMLAB /PENBMI toolbox
is similar to
pensdp , with added support for the bilinear
matrix inequalities.
3.2 Solver Routines in TOMLAB
3.2.1 TOMLAB Base Module
TOMLAB includes a large set of optimization solvers.
Most of them were originally developed by
the Applied Optimization and Modeling group (TOM) [
45].
Since then they have been improved e.g. to handle Matlab sparse
arrays and been further developed.
Table
3.2.1 lists the main set of TOM optimization solvers in all versions of TOMLAB .
|
|
| Function |
Description |
Section |
|
|
| clsSolve |
Constrained nonlinear least squares. Handles
simple bounds and linear equality and inequality constraints using
an active-set strategy. Implements Gauss-Newton, and hybrid
quasi-Newton and Gauss-Newton methods. |
11.1.1 |
|
| conSolve |
Constrained nonlinear minimization solver using
two different sequential quadratic programming methods. |
11.1.2 |
|
| cutplane |
Mixed-integer programming using a cutting plane
algorithm. |
11.1.3 |
| DualSolve |
Solves a linear program with a dual feasible
starting point. |
11.1.4 |
| expSolve |
Solves exponential fitting problems. |
11.1.5 |
| glbFast |
Box-bounded global optimization, using only
function values. Fortran MEX implementation of glbSolve . |
11.1.7 |
| glbSolve |
Box-bounded global optimization, using only
function values. |
11.1.8 |
| glcCluster |
Hybrid algorithm for constrained mixed-integer
global optimization. Uses a combination of glcFast (DIRECT)
and a clustering algorithm. |
11.1.9 |
| glcFast |
Box-bounded global optimization, using only
function values. Fortran MEX implementation of glcSolve . |
11.1.11 |
| glcSolve |
Global mixed-integer nonlinear programming,
using no derivatives. |
11.1.12 |
| infSolve |
Constrained minimax optimization. Reformulates
problem and calls any suitable nonlinear solver. |
11.1.14 |
| lpSimplex |
Linear programming using a simplex algorithm. |
11.1.16 |
| MILPSOLVE |
Mixed-integer programming using branch and bound. |
11.1.18 |
| L1Solve |
Constrained L1 optimization. Reformulates problem
and calls any suitable nonlinear solver. |
11.1.17 |
| mipSolve |
Mixed-integer programming using a
branch-and-bound algorithm. |
11.1.19 |
| nlpSolve |
Constrained nonlinear minimization solver using
a filter SQP algorithm. |
11.1.21 |
| pdco |
Linearly constrained nonlinear minimization solver
using a primal-dual barrier algorithm. |
11.1.22 |
| pdsco |
Linearly constrained nonlinear minimization solver
using a primal-dual barrier algorithm, for separable functions. |
11.1.23 |
| qpSolve |
Non-convex quadratic programming. |
11.1.24 |
| slsSolve |
Sparse constrained nonlinear least squares.
Reformulates problem and calls any suitable sparse nonlinear
solver. |
11.1.25 |
| sTrustr |
Constrained convex optimization of partially
separable functions, using a structural trust region algorithm. |
11.1.26 |
| ucSolve |
Unconstrained optimization with simple bounds on
the parameters. Implements Newton, quasi-Newton and
conjugate-gradient methods. |
11.1.27 |
| |
|
Additional Fortran solvers in TOMLAB v4.0 are listed in
Table
2.
They are
called using a set of MEX-file interfaces developed in TOMLAB .
Table 2: Additional solvers in TOMLAB Base Module v4.0 .
|
| Function |
Description |
Reference |
|
| goalSolve |
Solves sparse multi-objective goal attainment problems |
|
| lsei |
Dense constrained linear least squares |
|
| qld |
Convex quadratic programming |
|
| Tfzero |
Finding a zero to f(x) in an interval, x is one-dimensional. |
[73, 17] |
| Tlsqr |
Sparse linear least squares. |
[63, 62, 71] |
| Tnnls |
Nonnegative constrained linear least squares |
|
| |
|
3.2.2 TOMLAB /BARNLP
The add-on toolbox TOMLAB /BARNLP solves large-scale nonlinear
programming problems using a sparse primal-dual interior point
algorithm, in conjunction with a filter for globalization. The
solver package was developed in co-operation with Boeing Phantom
Works. The TOMLAB /BARNLP package is described in a separate manual
available at
http://tomopt.com.
3.2.3 TOMLAB /CGO
The add-on toolbox TOMLAB /CGO solves costly global optimization
problems. The solvers are listed in Table
3. They are
written in a combination of Matlab and Fortran code, where the
Fortran code is called using a set of MEX-file interfaces
developed in TOMLAB .
Table 3: Additional solvers in TOMLAB /CGO.
|
| Function |
Description |
Reference |
|
| rbfSolve |
Costly constrained box-bounded optimization
using a RBF algorithm. |
[9] |
| ego |
Costly constrained box-bounded optimization using the
Efficient Global Optimization (EGO) algorithm. |
[18] |
|
3.2.4 TOMLAB /CONOPT
The add-on toolbox TOMLAB /CONOPT solves large-scale nonlinear
programming problems with a feasible path GRG method . The solver
package was developed in co-operation with Arki Consulting and
Development A/S. The TOMLAB /CONOPT is described in a separate
manual available at
http://tomopt.com. There is also m-file
help available.
3.2.5 TOMLAB /CPLEX
The add-on toolbox TOMLAB /CPLEX solves large-scale mixed-integer
linear and quadratic programming problems. The solver package was
developed in co-operation with ILOG S.A. The TOMLAB /CPLEX solver
package and interface are described in a manual available at
http://tomopt.com.
3.2.6 TOMLAB /KNITRO
The add-on toolbox TOMLAB /KNITRO solves large-scale nonlinear
programming problems with interior (barrier) point trust-region
methods. The solver package was developed in co-operation with Ziena
Optimization Inc. The TOMLAB /KNITRO manual is available at
http://tomopt.com.
3.2.7 TOMLAB /LGO
The add-on toolbox TOMLAB /LGO solves global nonlinear programming
problems. The LGO solver package is developed by Pintér Consulting
Services, Inc. [
66] The TOMLAB /LGO manual is available
at
http://tomopt.com.
3.2.8 TOMLAB /MINLP
The add-on toolbox TOMLAB /MINLP provides solvers for continuous and
mixed-integer quadratic programming (
qp,
miqp) and
continuous and mixed-integer nonlinear constrained optimization
(
con,
minlp).
All four solvers, written by Roger Fletcher and Sven Leyffer,
University of Dundee, Scotland, are available in sparse and dense
versions. The solvers are listed in Table
4.
The TOMLAB /MINLP manual is available at
http://tomopt.com.
Table 4: Solver routines in TOMLAB /MINLP .
|
| Function |
Description |
Reference |
|
| bqpd |
Quadratic programming using a null-space method. |
bqpdTL.m |
| |
| miqpBB |
Mixed-integer quadratic programming using bqpd as subsolver. |
miqpBBTL.m |
| |
| filterSQP |
Constrained nonlinear minimization using a Filtered Sequential QP method. |
filterSQPTL.m |
| |
| minlpBB |
Constrained, mixed-integer nonlinear minimization using a branch-and-bound
search scheme. filterSQP is used as NLP solver. |
minlpBBTL.m |
|
3.2.9 TOMLAB /MINOS
Another set of Fortran solvers were developed by the Stanford
Optimization Laboratory (SOL). Table
5 lists the
solvers included in TOMLAB /MINOS. The solvers are called using a
set of MEX-file interfaces developed as part of TOMLAB . All
functionality of the SOL solvers are available and changeable in
the TOMLAB framework in Matlab .
Table 5: The SOL optimization solvers in TOMLAB /MINOS .
|
| Function |
Description |
Reference |
Page |
|
| MINOS 5.51 |
Sparse linear and nonlinear programming with
linear and nonlinear constraints. |
[60] |
|
| LP-MINOS |
A special version of the MINOS 5.5
MEX-file interface for sparse linear programming. |
[60] |
|
| QP-MINOS |
A special version of the MINOS 5.5
MEX-file interface for sparse quadratic programming. |
[60] |
|
| LPOPT 1.0-10 |
Dense linear programming. |
[33] |
|
| QPOPT 1.0-10 |
Non-convex quadratic programming with dense
constraint matrix and sparse or dense quadratic matrix. |
[33] |
|
|
3.2.10 TOMLAB /OQNLP
The add-on toolbox Tomlab /OQNLP uses a multistart heuristic
algorithm to find global optima of smooth constrained nonlinear
programs (NLPs) and mixed-integer nonlinear programs (MINLPs). The
solver package was developed in co-operation with Optimal Methods
Inc. The TOMLAB /OQNLP manual is available at
http://tomopt.com.
3.2.11 TOMLAB /NLPQL
The add-on toolbox TOMLAB /NLPQL solves dense nonlinear programming
problems, multi criteria optimization problems and nonlinear fitting
problems. The solver package was developed in co-operation with
Klaus Schittkowski. The TOMLAB /NLPQL manual is available at
http://tomopt.com.
3.2.12 TOMLAB /NPSOL
The add-on toolbox TOMLAB /NPSOL is a sub package of TOMLAB /SOL.
The package includes the MINOS solvers as well as NPSOL, LSSOL and
NLSSOL. The TOMLAB /NPSOL manual is available at
http://tomopt.com.
3.2.13 TOMLAB /PENBMI
The add-on toolbox TOMLAB /PENBMI solves linear semi-definite
programming problems with linear and bilinear matrix inequalities.
The solvers are listed in Table
6. They are written in a
combination of Matlab and C code. The TOMLAB /PENBMI manual is
available at
http://tomopt.com.
Table 6: Additional solvers in TOMLAB /PENSDP.
|
| Function |
Description |
Reference |
Page |
|
| penbmi |
Sparse and dense linear semi-definite programming using a penalty algorithm. |
|
|
| penfeas_bmi |
Feasibility check of systems of
linear matrix inequalities, using penbmi . |
|
|
|
3.2.14 TOMLAB /PENSDP
The add-on toolbox TOMLAB /PENSDP solves linear semi-definite
programming problems with linear matrix inequalities. The solvers
are listed in Table
7. They are written in a combination
of Matlab and C code. The TOMLAB /PENSDP manual is available at
http://tomopt.com.
Table 7: Additional solvers in Tomlab /PENSDP.
|
| Function |
Description |
Reference |
Page |
|
| pensdp |
Sparse and dense linear semi-definite programming using a penalty algorithm. |
|
|
| penfeas_sdp |
Feasibility check of systems of
linear matrix inequalities, using pensdp . |
|
|
|
3.2.15 TOMLAB /SNOPT
The add-on toolbox TOMLAB /SNOPT is a sub package of TOMLAB /SOL.
The package includes the MINOS solvers as well as SNOPT and SQOPT.
The TOMLAB /SNOPT manual is available at
http://tomopt.com.
The extension toolbox TOMLAB /SOL gives access to the complete set of
Fortran solvers developed by the Stanford Systems Optimization
Laboratory (SOL). These solvers are listed in Table
5 and
8.
Table 8: The optimization solvers in the TOMLAB /SOL toolbox.
|
| Function |
Description |
Reference |
Page |
|
| NPSOL 5.02 |
Dense linear and nonlinear programming with
linear and nonlinear constraints. |
[37] |
|
| SNOPT 6.2-2 |
Large, sparse linear and nonlinear
programming with linear and nonlinear constraints. |
[36, 34] |
|
| SQOPT 6.2-2 |
Sparse convex quadratic programming. |
[35] |
|
| NLSSOL 5.0-2 |
Constrained nonlinear least squares. NLSSOL
is based on NPSOL. No reference except for general NPSOL
reference. |
[37] |
|
| LSSOL 1.05-4 |
Dense linear and quadratic programs
(convex), and constrained linear least squares problems. |
[32] |
|
|
3.2.17 TOMLAB /SPRNLP
The add-on toolbox TOMLAB /SPRNLP solves large-scale nonlinear
programming problems. SPRNLP is a state-of-the-art sequential
quadratic programming (SQP) method, using an augmented Lagrangian
merit function and safeguarded line search. The solver package was
developed in co-operation with Boeing Phantom Works. The TOMLAB
/SPRNLP package is described in a separate manual available at
http://tomopt.com.
The add-on toolbox TOMLAB /XA solves large-scale linear, binary,
integer and semi-continuous linear programming problems, as well as
quadratic programming problems. The solver package was developed in
co-operation with Sunset Software Technology. The TOMLAB /XA package
is described in a separate manual available at
http://tomopt.com.
3.2.19 TOMLAB /Xpress
The add-on toolbox TOMLAB /Xpress solves large-scale mixed-integer
linear and quadratic programming problems. The solver package was
developed in co-operation with Dash Optimization Ltd. The TOMLAB
/Xpress solver package and interface are described in the html
manual that comes with the installation package. There is also a
TOMLAB /Xpress manual available at
http://tomopt.com.
3.2.20 Finding Available Solvers
To get a list of all available solvers, including Fortran, C and
Matlab Optimization Toolbox solvers, for a certain
solvType ,
call the routine
SolverList with
solvType as argument.
solvType should either be a string ('uc', 'con' etc.) or the
corresponding
solvType number as given in
Table
2.2.
For example, if wanting a list of all
available solvers of
solvType con, then
SolverList('con')
gives the output
>> SolverList('con');
Tomlab recommended choice for Constrained Nonlinear Programming (NLP)
npsol
Other solvers for NLP
Licensed:
nlpSolve
conSolve
sTrustr
constr
minos
snopt
fmincon
filterSQP
PDCO
PDSCO
Non-licensed:
NONE
Solvers also handling NLP
Licensed:
glcSolve
glcFast
glcCluster
rbfSolve
minlpBB
Non-licensed:
NONE
SolverList also returns two output arguments: all available
solvers as a string matrix and a vector with the corresponding
solvType for each solver.
Note that solvers for a more general problem type
may be used to solve the problem.
In Table
9 an attempt has been made to
classify these relations.
Table 9: The problem classes (probType)
possible to solve with each type of solver (solvType)
is marked with an x. When the solver is in theory
possible to use, but from a practical point of view is probably
not suitable, parenthesis are added (x).
| |
solvType |
| probType |
uc |
qp |
con |
ls |
lls |
cls |
mip |
lp |
glb |
glc |
| uc |
x |
|
x |
|
|
|
|
|
x |
(x) |
|
| qp |
|
x |
x |
|
|
|
|
|
|
(x) |
|
| con |
|
|
x |
|
|
|
|
|
|
(x) |
|
| ls |
|
|
x |
x |
|
x |
|
|
|
(x) |
|
| lls |
|
x |
x |
x |
x |
x |
|
|
|
(x) |
|
| cls |
|
|
x |
|
|
x |
|
|
|
(x) |
|
| mip |
|
|
|
|
|
|
x |
|
|
(x) |
|
| lp |
|
x |
x |
|
|
|
x |
x |
|
(x) |
|
| glb |
|
|
(x) |
|
|
|
|
|
x |
x |
|
| glc |
|
|
(x) |
|
|
|
|
|
|
x |
|
| exp |
x |
|
x |
(x) |
|
x |
|
|
|
(x) |
|
« Previous « Start » Next »
 Rn and f(x)
Rn and f(x)  R. For unbounded variables, the corresponding elements of xL,xU may be set to ± ∞.
R. For unbounded variables, the corresponding elements of xL,xU may be set to ± ∞. Rn, F
Rn, F  Rn × n,
A
Rn × n,
A  Rm1 × n, and bL,bU
Rm1 × n, and bL,bU  Rm1.
Rm1. Rn, f(x)
Rn, f(x)  R, A
R, A
 Rm1 × n, bL,bU
Rm1 × n, bL,bU  Rm1
and cL,c(x),cU
Rm1
and cL,c(x),cU  Rm2.
Rm2. Rn, f(x)
Rn, f(x)  R, i.e.
problems of the form (1) that have finite simple bounds on
all variables.
R, i.e.
problems of the form (1) that have finite simple bounds on
all variables. Rn, f(x)
Rn, f(x)  R, A
R, A
 Rm1 × n, bL,bU
Rm1 × n, bL,bU  Rm1
and cL,c(x),cU
Rm1
and cL,c(x),cU  Rm2.
The variables x
Rm2.
The variables x  I, the index subset of 1,...,n, are restricted to be
integers.
I, the index subset of 1,...,n, are restricted to be
integers. Rn,
A
Rn,
A  Rm1 × n, and bL,bU
Rm1 × n, and bL,bU  Rm1.
Rm1. Rn, A
Rn, A  Rm1
× n, and bL,bU
Rm1
× n, and bL,bU  Rm1. The variables x
Rm1. The variables x
 I, the index subset of 1,...,n are restricted to be
integers. Equality constraints are defined by setting the lower
bound equal to the upper bound, i.e. for constraint i: bL(i)
= bU(i).
I, the index subset of 1,...,n are restricted to be
integers. Equality constraints are defined by setting the lower
bound equal to the upper bound, i.e. for constraint i: bL(i)
= bU(i). Rn, d
Rn, d  RM,
C
RM,
C  RM × n,
A
RM × n,
A  Rm1 × n, bL,bU
Rm1 × n, bL,bU  Rm1
and cL,c(x),cU
Rm1
and cL,c(x),cU  Rm2.
Rm2. Rn, r(x)
Rn, r(x)  RM,
A
RM,
A  Rm1 × n, bL,bU
Rm1 × n, bL,bU  Rm1
and cL,c(x),cU
Rm1
and cL,c(x),cU  Rm2.
Rm2. Rn, A
Rn, A  Rml
× n, bL,bU
Rml
× n, bL,bU  Rml and Qki are
symmetric matrices of similar dimensions in each constraint i.
If there are several LMI constraints, each may have it's own dimension.
Rml and Qki are
symmetric matrices of similar dimensions in each constraint i.
If there are several LMI constraints, each may have it's own dimension.