« Previous « Start » Next »
12 Batch Production
Dynamic optimization of bioprocesses: efficient and robust numerical strategies 2003, Julio R. Banga, Eva Balsa-Cantro, Carmen G. Moles and Antonio A. Alonso
Case Study II: Optimal Control of a Fed-Batch Reactor for Ethanol Production
12.1 Problem description
This case study considers a fed-batch reactor for the production of ethanol, as studied by Chen and Hwang (1990a) and others (Bojkov & Luus 1996, Banga et al. 1997). The (free terminal time) optimal control problem is to maximize the yield of ethanol using the feed rate as the control variable. As in the previous case, this problem has been solved using CVP and gradient based methods, but convergence problems have been frequently reported, something which has been confirmed by our own experience. The mathematical statement of the free terminal time problem is:
Find the feed flow rate u(t) and the final time t_f over t in [t0; t_f ] to maximize
subject to:
where x1, x2 and x3 are the cell mass, substrate and product concentrations (g/L), and x4 is the volume (L). The initial conditions are:
The constraints (upper and lower bounds) on the control variable (feed rate, L/h) are:
and there is an end-point constraint on the volume:
Reference: [3]
12.2 Problem setup
toms t
toms tfs
t_f = 100*tfs;
% initial guesses
tfg = 60;
x1g = 10;
x2g = 150-150*t/t_f;
x3g = 70;
x4g = 200*t/t_f;
ug = 3;
n = [ 20 60 60 60];
e = [0.01 0.002 1e-4 0];
for i = 1:3
p = tomPhase('p', t, 0, t_f, n(i));
setPhase(p);
tomStates x1s x2s x3s x4s
if e(i)
tomStates u
else
tomControls u
end
%tomControls g1 g2
% Create scaled states, to make the numeric solver work better.
x1 = 10*x1s;
x2 = 1*x2s;
x3 = 100*x3s;
x4 = 100*x4s;
% Initial guess
% Note: The guess for t_f must appear in the list before expression involving t.
x0 = {t_f == tfg
icollocate({
x1 == x1g
x2 == x2g
x3 == x3g
x4 == x4g
})
collocate({u==ug})};
% Box constraints
cbox = {
0.1 <= t_f <= 100
mcollocate({
0 <= x1
0 <= x2
0 <= x3
1e-8 <= x4 % Avoid division by zero.
})
0 <= collocate(u) <= 12};
% Boundary constraints
cbnd = {initial({
x1 == 1;
x2 == 150
x3 == 0;
x4 == 10})
final(0 <= x4 <= 200)};
% Various constants and expressions
g1 = (0.408/(1+x3/16))*(x2/(x2+0.22));
g2 = (1/(1+x3/71.5))*(x2/(0.44+x2));
% ODEs and path constraints
ceq = collocate({
dot(x1) == g1*x1 - u*x1/x4
dot(x2) == -10*g1*x1 + u*(150-x2)/x4
dot(x3) == g2*x1 - u*x3/x4
dot(x4) == u});
% Objective
J = final(x3*x4);
if e(i)
% Add cost on oscillating u.
objective = -J/4900 + e(i)*integrate(dot(u)^2);
else
objective = -J/4900;
end
12.3 Solve the problem
options = struct;
options.name = 'Batch Production';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
Problem type appears to be: con
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Batch Production f_k -4.131438264402751400
sum(|constr|) 0.316463714336870480
f(x_k) + sum(|constr|) -3.814974550065881200
f(x_0) 1.259999999999963600
Solver: snopt. EXIT=1. INFORM=32.
SNOPT 7.2-5 NLP code
Major iteration limit reached
FuncEv 4791 GradEv 4789 ConstrEv 4789 ConJacEv 4789 Iter 1000 MinorIter 5646
CPU time: 22.078125 sec. Elapsed time: 22.469000 sec.
Warning: Solver returned ExitFlag = 1
The returned solution may be incorrect.
Problem type appears to be: con
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Batch Production f_k -4.222925108597277000
sum(|constr|) 0.000004304588346354
f(x_k) + sum(|constr|) -4.222920804008930800
f(x_0) -1.781431131250453600
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 517 GradEv 515 ConstrEv 515 ConJacEv 515 Iter 455 MinorIter 988
CPU time: 17.078125 sec. Elapsed time: 17.484000 sec.
Problem type appears to be: con
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Batch Production f_k -4.248461985888144300
sum(|constr|) 0.000062226344424072
f(x_k) + sum(|constr|) -4.248399759543720400
f(x_0) -4.126187662864473400
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 277 GradEv 275 ConstrEv 275 ConJacEv 275 Iter 191 MinorIter 624
CPU time: 7.843750 sec. Elapsed time: 7.985000 sec.
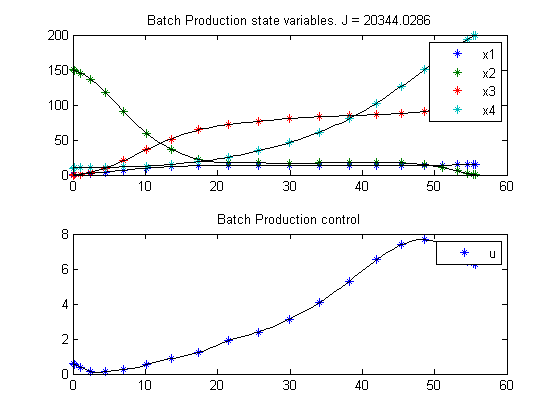
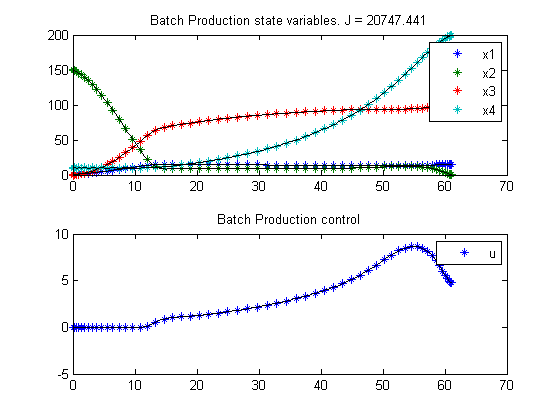
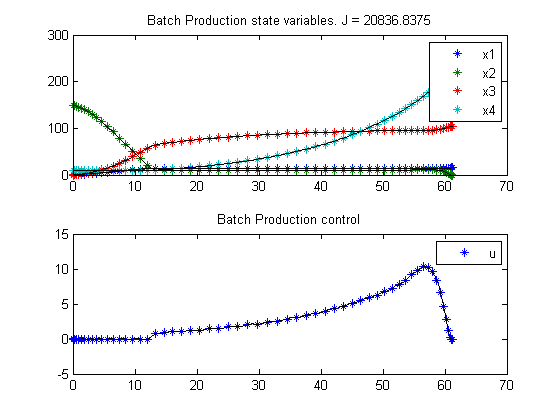
12.4 Plot result
subplot(2,1,1)
ezplot([x1 x2 x3 x4]);
legend('x1','x2','x3','x4');
title(['Batch Production state variables. J = ' num2str(subs(J,solution))]);
subplot(2,1,2)
ezplot(u);
legend('u');
title('Batch Production control');
drawnow
% Copy inital guess for next iteration
tfg = subs(t_f,solution);
x1g = subs(x1,solution);
x2g = subs(x2,solution);
x3g = subs(x3,solution);
x4g = subs(x4,solution);
end
« Previous « Start » Next »