« Previous « Start » Next »
43 Goddard Rocket, Maximum Ascent
Benchmarking Optimization Software with COPS Elizabeth D. Dolan and Jorge J. More ARGONNE NATIONAL LABORATORY
43.1 Problem Formulation
Find u(t) over t in [0; T ] to minimize
subject to:
Reference: [14]
43.2 Problem setup
toms t
toms t_f
43.3 Solve the problem, using a successively larger number collocation points
for n=[20 50 100]
p = tomPhase('p', t, 0, t_f, n);
setPhase(p);
tomStates v h m
tomControls T
% Initial guess
if n==20
x0 = {t_f == 1
icollocate({v == 620; h == 1
m == 1-0.4*t/t_f})
collocate(T == 0)};
else
x0 = {t_f == tfopt
icollocate({v == vopt; h == hopt
m == mopt})
collocate(T == Topt)};
end
% Box constraints
cbox = {0.1 <= t_f <= 1
icollocate({
0 <= v; 1 <= h
0.6 <= m <= 1
0 <= T <= 3.5})};
% Boundary constraints
cbnd = {initial({v == 0; h == 1; m == 1})
final({m == 0.6})};
b = 500;
D = 0.5*620*v.^2.*exp(-b*h);
g = 1./h.^2;
c = 0.5;
% ODEs and path constraints
ceq = collocate({dot(v) == (T-D)./m-g
dot(h) == v; dot(m) == -T/c});
% Objective
objective = -final(h);
43.4 Solve the problem
options = struct;
options.name = 'Goddard Rocket';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
% Optimal v and more to use as starting guess
vopt = subs(v, solution);
hopt = subs(h, solution);
mopt = subs(m, solution);
Topt = subs(T, solution);
tfopt = subs(t_f, solution);
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Goddard Rocket f_k -1.025133414041158100
sum(|constr|) 0.000002519458500791
f(x_k) + sum(|constr|) -1.025130894582657400
f(x_0) -0.999999999999998220
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 41 ConJacEv 41 Iter 23 MinorIter 1196
CPU time: 0.187500 sec. Elapsed time: 0.188000 sec.
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Goddard Rocket f_k -1.025311927458321800
sum(|constr|) 0.000016009289221361
f(x_k) + sum(|constr|) -1.025295918169100400
f(x_0) -1.025133225224282200
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 23 ConJacEv 23 Iter 14 MinorIter 550
CPU time: 0.312500 sec. Elapsed time: 0.312000 sec.
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Goddard Rocket f_k -1.025328777109889600
sum(|constr|) 0.000000000007939354
f(x_k) + sum(|constr|) -1.025328777101950100
f(x_0) -1.025311927458318500
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 12 ConJacEv 12 Iter 7 MinorIter 553
CPU time: 0.765625 sec. Elapsed time: 0.797000 sec.
end
t = subs(collocate(t),solution);
v = subs(collocate(vopt),solution);
h = subs(collocate(hopt),solution);
m = subs(collocate(mopt),solution);
T = subs(collocate(Topt),solution);
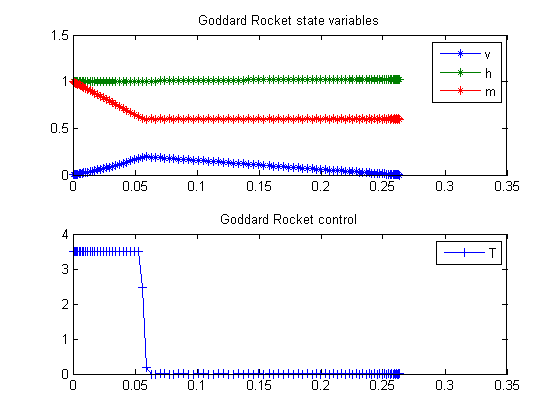
43.5 Plot result
subplot(2,1,1)
plot(t,v,'*-',t,h,'*-',t,m,'*-');
legend('v','h','m');
title('Goddard Rocket state variables');
subplot(2,1,2)
plot(t,T,'+-');
legend('T');
title('Goddard Rocket control');
« Previous « Start » Next »