« Previous « Start » Next »
53 Isometrization of alpha pinene
Benchmarking Optimization Software with COPS Elizabeth D. Dolan and Jorge J. More ARGONNE NATIONAL LABORATORY
53.1 Problem Formulation
Find theta over t in [0; 40000 ] to minimize
subject to:
| = theta2*y1−(theta3+theta4)*y3+theta5*y5 |
| timemeas = [1230 3060 4920 7800 10680 15030 22620 36420] |
| y1meas = [88.35 76.4 65.1 50.4 37.5 25.9 14.0 4.5] |
| y2meas = [7.3 15.6 23.1 32.9 42.7 49.1 57.4 63.1] |
| y3meas = [2.3 4.5 5.3 6.0 6.0 5.9 5.1 3.8] |
| y4meas = [0.4 0.7 1.1 1.5 1.9 2.2 2.6 2.9] |
| y5meas = [1.75 2.8 5.8 9.3 12.0 17.0 21.0 25.7] |
Reference: [14]
53.2 Problem setup
toms t theta1 theta2 theta3 theta4 theta5
53.3 Solve the problem, using a successively larger number collocation points
for n=[20 50]
p = tomPhase('p', t, 0, 40000, n);
setPhase(p);
tomStates y1 y2 y3 y4 y5
% Initial guess
if n == 20
x0 = {theta1 == 0; theta2 == 0
theta3 == 0; theta4 == 0
theta5 == 0; icollocate({
y1 == 100; y2 == 0
y3 == 0; y4 == 0
y5 == 0})};
else
x0 = {theta1 == theta1opt; theta2 == theta2opt
theta3 == theta3opt; theta4 == theta4opt
theta5 == theta5opt; icollocate({
y1 == y1opt; y2 == y2opt
y3 == y3opt; y4 == y4opt
y5 == y5opt})};
end
% Box constraints
cbox = {0 <= theta1; 0 <= theta2; 0 <= theta3
0 <= theta4; 0 <= theta5};
% Boundary constraints
cbnd = initial({y1 == 100; y2 == 0
y3 == 0; y4 == 0; y5 == 0});
y1meas = [88.35; 76.4; 65.1; 50.4; 37.5; 25.9; 14.0; 4.5];
y2meas = [7.3; 15.6; 23.1; 32.9; 42.7; 49.1; 57.4; 63.1];
y3meas = [2.3; 4.5; 5.3; 6.0; 6.0; 5.9; 5.1; 3.8];
y4meas = [0.4; 0.7; 1.1; 1.5; 1.9; 2.2; 2.6; 2.9];
y5meas = [1.75; 2.8; 5.8; 9.3; 12.0; 17.0; 21.0; 25.7];
tmeas = [1230; 3060; 4920; 7800; 10680; 15030; 22620; 36420];
y1err = sum((atPoints(tmeas,y1) - y1meas).^2);
y2err = sum((atPoints(tmeas,y2) - y2meas).^2);
y3err = sum((atPoints(tmeas,y3) - y3meas).^2);
y4err = sum((atPoints(tmeas,y4) - y4meas).^2);
y5err = sum((atPoints(tmeas,y5) - y5meas).^2);
% ODEs and path constraints
ceq = collocate({
dot(y1) == -(theta1+theta2)*y1
dot(y2) == theta1*y1
dot(y3) == theta2*y1-(theta3+theta4)*y3+theta5*y5
dot(y4) == theta3*y3
dot(y5) == theta4*y3-theta5*y5});
% Objective
objective = y1err+y2err+y3err+y4err+y5err;
53.4 Solve the problem
options = struct;
options.name = 'Isometrization of alpha pinene';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
% Optimal y and theta - starting guess in the next iteration
y1opt = subs(y1, solution);
y2opt = subs(y2, solution);
y3opt = subs(y3, solution);
y4opt = subs(y4, solution);
y5opt = subs(y5, solution);
theta1opt = subs(theta1, solution);
theta2opt = subs(theta2, solution);
theta3opt = subs(theta3, solution);
theta4opt = subs(theta4, solution);
theta5opt = subs(theta5, solution);
Problem type appears to be: qpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Isometrization of alpha pinene f_k 19.872166933768312000
sum(|constr|) 0.000000000005482115
f(x_k) + sum(|constr|) 19.872166933773794000
f(x_0) 7569.999999999995500000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 74 ConJacEv 74 Iter 57 MinorIter 239
CPU time: 0.343750 sec. Elapsed time: 0.391000 sec.
Problem type appears to be: qpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Isometrization of alpha pinene f_k 19.872166934168490000
sum(|constr|) 0.000000000010589892
f(x_k) + sum(|constr|) 19.872166934179081000
f(x_0) -38011.572833066202000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 15 ConJacEv 15 Iter 11 MinorIter 263
CPU time: 0.328125 sec. Elapsed time: 0.359000 sec.
end
t = subs(collocate(t),solution);
y1 = collocate(y1opt);
y2 = collocate(y2opt);
y3 = collocate(y3opt);
y4 = collocate(y4opt);
y5 = collocate(y5opt);
53.5 Plot result
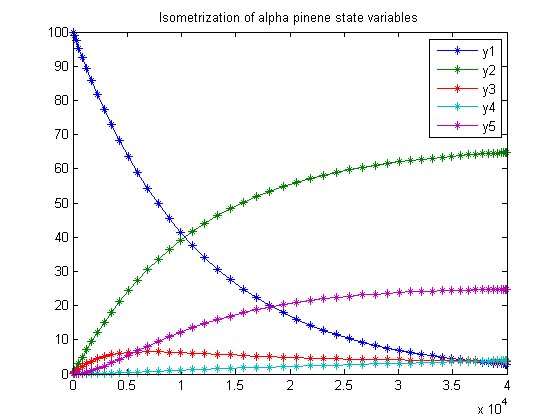
figure(1)
plot(t,y1,'*-',t,y2,'*-',t,y3,'*-',t,y4,'*-',t,y5,'*-');
legend('y1','y2','y3','y4','y5');
title('Isometrization of alpha pinene state variables');
« Previous « Start » Next »