« Previous « Start » Next »

34  Euler Buckling Problem

Problem 4: Miser3 manual

34.1  Problem description

Over t in [0; 1 ], minimize

J = −z1

subject to:

dx1 dt

= x2

dx2 dt

=

−z1*x1 x32

∫

1 0

x3(t) dt − 1 = 0

x1(0) = 0

x1(1) = 0

x2(0) = 1

x3(0) >= 0.5

x3(t) >= 0.5

Reference: [19]

34.2  Problem setup

toms t
toms z1
p = tomPhase('p', t, 0, 1, 40);
setPhase(p);

% States
tomStates x1 x2 x3 x4
% We don't need to introduce any control variables.

% Initial guess
x0 = {icollocate({
    x1 == 0;   x2 == 1
    x3 == 0.5; x4 == t/40})
    z1 == 10};

% Box constraints
cbox = {
    icollocate({-10 <= x1 <= 10
    -10 <= x2 <= 10; 0.5 <= x3 <= 10})
      0 <= z1 <= 500};

% Boundary constraints
cbnd = {initial({x3 >= 0.5; x1 == 0
    x2 == 1; x4 == 0})
    final({x1 == 0; x4 == 1})};

% ODEs and path constraints
ceq = {collocate({
    dot(x1) == x2
    dot(x2) == -z1*x1./x3.^2
    x3 >= 0.5 % Path constr.
     % Integral constr.
    })
    integrate(x3) == 1};

% Objective
objective = z1;

34.3  Solve the problem

options = struct;
options.name = 'Euler Buckling';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

% Extract optimal states and controls from solution
t  = subs(collocate(t),solution);
x1 = subs(collocate(x1),solution);
x2 = subs(collocate(x2),solution);
x3 = subs(collocate(x3),solution);

Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2011-02-05
=====================================================================================
Problem: ---  1: Euler Buckling                 f_k       9.881895688695376400
                                       sum(|constr|)      0.000000016445563739
                              f(x_k) + sum(|constr|)      9.881895705140939500
                                              f(x_0)     10.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv   73 ConJacEv   72 Iter   33 MinorIter  239
CPU time: 0.187500 sec. Elapsed time: 0.188000 sec.

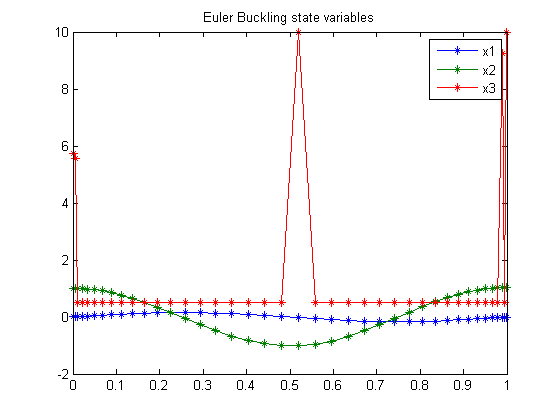
34.4  Plot result

figure(1)
plot(t,x1,'*-',t,x2,'*-',t,x3,'*-');
legend('x1','x2','x3');
title('Euler Buckling state variables');

34.5  Footnote

In the original [Miser3] problem formulation, it is requested to compute "u", equal to x3_t. u is not included in the optimization problem, thereby speeding up the solution process. x3_t can be obtained by simple numeric differentiation of x3.

Note, however, that because there was no constraint on u, and it was not included in the cost function, x3_t looks very strange.

« Previous « Start » Next »