« Previous « Start » Next »
78 Orbit Raising Maximum Radius
78.1 Problem description
Maximize:
subject to the dynamic constraints
the boundary conditions
and the path constraint
The control pitch angel is not being used in this formulation. Instead two control variables (w1,w2) are used to for the thrust direction. A path constraint ensures that (w1,w2) is a unit vector.
Reference: [5]
78.2 Problem setup
t_F = 3.32;
mmu = 1;
m_0 = 1; r_0 = 1; u_0 = 0;
u_f = 0; v_0 = sqrt(mmu/r_0); rmin = 0.9;
rmax = 5; umin = -5; umax = 5;
vmin = -5; vmax = 5; mmax = m_0;
mmin = 0.1;
T = 0.1405;
Ve = 1.8758;
toms t
p1 = tomPhase('p1', t, 0, t_F, 40);
setPhase(p1);
tomStates r u v m
tomControls w1 w2
% Initial guess
x0 = {icollocate({
r == r_0
u == u_0 + (u_f-u_0)*t/t_F
v == v_0
m == m_0})
collocate({w1 == 0; w2 == 1})};
% Boundary constraints
cbnd = {initial({
r == r_0
u == u_0
v == v_0
m == m_0
})
final({u == u_f
v - sqrt(mmu/r) == 0})};
% Box constraints
cbox = {
rmin <= icollocate(r) <= rmax
umin <= icollocate(u) <= umax
vmin <= icollocate(v) <= vmax
mmin <= icollocate(m) <= mmax
-1 <= collocate(w1) <= 1
-1 <= collocate(w2) <= 1};
% ODEs and path constraints
ceq = collocate({
dot(r) == u
dot(u) == v^2/r-mmu/r^2+T*w1/m
dot(v) == -u*v/r+T*w2/m
dot(m) == -T/Ve
w1^2+w2^2 == 1});
% Objective
objective = -final(r);
78.3 Solve the problem
options = struct;
options.name = 'Orbit Raising Problem Max Radius';
options.solver = 'snopt';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Orbit Raising Problem Max Radius f_k -1.518744202740336600
sum(|constr|) 0.000017265841651215
f(x_k) + sum(|constr|) -1.518726936898685300
f(x_0) -0.999999999999991120
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 59 ConJacEv 59 Iter 36 MinorIter 346
CPU time: 0.656250 sec. Elapsed time: 0.656000 sec.
78.4 Plot result
subplot(2,1,1)
ezplot([r u v m]);
legend('r','u','v','m');
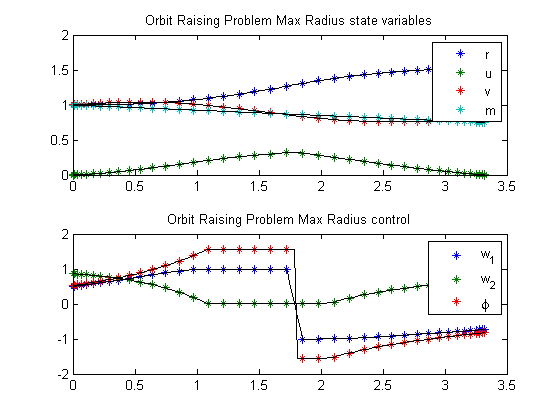
title('Orbit Raising Problem Max Radius state variables');
subplot(2,1,2)
ezplot([w1 w2 atan2(w1,w2)])
legend('w_1', 'w_2', '\phi');
title('Orbit Raising Problem Max Radius control');
« Previous « Start » Next »