« Previous « Start » Next »

15  The Brachistochrone Problem (DAE formulation)

We will now solve the same problem as in brachistochrone.m, but using a DAE formulation for the mechanics.

15.1  DAE formulation

In a DAE formulation we don’t need to formulate explicit equations for the time-derivatives of each state. Instead we can, for example, formulate the conservation of energy.

Ekin =

m 2

dx dt

2 +

dx dt

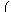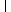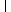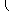2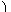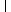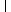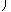

,

Epot = m g y .

The boundary conditions are still A = (0,0), B = (10,-3), and an initial speed of zero, so we have

Ekin + Epot = 0

For complex mechanical systems, this freedom to choose the most convenient formulation can save a lot of effort in modelling the system. On the other hand, computation times may get longer, because the problem can to become more non-linear and the jacobian less sparse.

Reference: [6]

15.2  Problem setup

toms t
toms t_f

p = tomPhase('p', t, 0, t_f, 20);
setPhase(p);

tomStates x y

% Initial guess
x0 = {t_f == 10};

% Box constraints
cbox = {0.1 <= t_f <= 100};

% Boundary constraints
cbnd = {initial({x == 0; y == 0})
    final({x == 10; y == -3})};

% Expressions for kinetic and potential energy
m = 1;
g = 9.81;
Ekin = 0.5*m*(dot(x).^2+dot(y).^2);
Epot = m*g*y;
v = sqrt(2/m*Ekin);

% ODEs and path constraints
ceq = collocate(Ekin + Epot == 0);

% Objective
objective = t_f;

15.3  Solve the problem

options = struct;
options.name = 'Brachistochrone-DAE';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
x  = subs(collocate(x),solution);
y  = subs(collocate(y),solution);
v  = subs(collocate(v),solution);
t  = subs(collocate(t),solution);

Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2011-02-05
=====================================================================================
Problem: ---  1: Brachistochrone-DAE            f_k       1.869963310229847400
                                       sum(|constr|)      0.000000000158881015
                              f(x_k) + sum(|constr|)      1.869963310388728300
                                              f(x_0)     10.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv  168 ConJacEv  168 Iter   93 MinorIter  154
CPU time: 0.203125 sec. Elapsed time: 0.219000 sec.

15.4  Plot the result

To obtain the brachistochrone curve, we plot y versus x.

subplot(2,1,1)
plot(x, y);
title('Brachistochrone, y vs x');

subplot(2,1,2)
plot(t, v);

« Previous « Start » Next »