« Previous « Start » Next »
73 Nonlinear CSTR
Dynamic optimization of chemical and biochemical processes using restricted second-order information 2001, Eva Balsa-Canto, Julio R. Banga, Antonio A. Alonso Vassilios S. Vassiliadis
Case Study III: Nonlinear CSTR
73.1 Problem description
The problem was first introduced by Jensen (1964) and consists of determining the four optimal controls of a chemical reactor in order to obtain maximum economic benefit. The system dynamics describe four simultaneous chemical reactions taking place in an isothermal continuous stirred tank reactor. The controls are the flow rates of three feed streams and an electrical energy input used to promote a photochemical reaction. Luus (1990) and Bojkov, Hansel, and Luus (1993) considered two sub-cases using three and four control variables respectively.
The problem is formulated as follows:Find u1(t), u2(t), u3(t) and u4(t) over t in [t0,t_f] to maximize:
Subject to:
| = u4−q*x1−17.6*x1*x2−23*x1*x6*u3 |
| = u1−q*x2−17.6*x1*x2−146*x2*x3 |
| = −q*x4+35.2*x1*x2−51.3*x4*x5 |
| = −q*x5+219*x2*x3−51.3*x4*x5 |
| = −q*x6+102.6*x4.*x5−23*x1*x6*u3 |
| = 5.8*(q*x1−u4)−3.7*u1−4.1*u2+ |
| q*(23*x4+11*x5+28*x6+35*x7)−5*u32−0.099 |
where:
with the initial conditions:
| x(t0) = [0.1883 0.2507 0.0467 0.0899 0.1804 0.1394 0.1046 0.000]′ |
And the following bounds on the control variables:
The final time is considered fixed as t_f = 0.2.
Reference: [1]
73.2 Problem setup
toms t
73.3 Solve the problem, using a successively larger number collocation points
for n=[5 20 60]
p = tomPhase('p', t, 0, 0.2, n);
setPhase(p);
tomStates x1 x2 x3 x4 x5 x6 x7 x8
tomControls u1 u2 u3 u4
% Interpolate an initial guess for the n collocation points
if n == 5
x0 = {};
else
x0 = {icollocate({x1 == x1opt; x2 == x2opt
x3 == x3opt; x4 == x4opt; x5 == x5opt
x6 == x6opt; x7 == x7opt; x8 == x8opt})
collocate({u1 == u1opt; u2 == u2opt
u3 == u3opt; u4 == u4opt})};
end
% Box constraints
cbox = {icollocate({
0 <= x1; 0 <= x2; 0 <= x3
0 <= x4; 0 <= x5; 0 <= x6
0 <= x7; 0 <= x8})
collocate({
0 <= u1 <= 20; 0 <= u2 <= 6
0 <= u3 <= 4; 0 <= u4 <= 20})};
% Boundary constraints
cbnd = initial({x1 == 0.1883; x2 == 0.2507
x3 == 0.0467; x4 == 0.0899; x5 == 0.1804
x6 == 0.1394; x7 == 0.1064; x8 == 0});
% ODEs and path constraints
% 4.1*u2+(u1+u2.*u4) in another paper, -0.09 instead of -0.099
q = u1+u2+u4;
ceq = collocate({
dot(x1) == (u4-q.*x1-17.6*x1.*x2-23*x1.*x6.*u3)
dot(x2) == (u1-q.*x2-17.6*x1.*x2-146*x2.*x3)
dot(x3) == (u2-q.*x3-73*x2.*x3)
dot(x4) == (-q.*x4+35.2*x1.*x2-51.3*x4.*x5)
dot(x5) == (-q.*x5+219*x2.*x3-51.3*x4.*x5)
dot(x6) == (-q.*x6+102.6*x4.*x5-23*x1.*x6.*u3)
dot(x7) == (-q.*x7+46*x1.*x6.*u3)
dot(x8) == (5.8*(q.*x1-u4)-3.7*u1-4.1*u2+q.*...
(23*x4+11*x5+28*x6+35*x7)-5*u3.^2-0.099)});
% Objective
objective = -final(x8);
73.4 Solve the problem
options = struct;
options.name = 'Nonlinear CSTR';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
% Optimal x and u as starting point
x1opt = subs(x1, solution);
x2opt = subs(x2, solution);
x3opt = subs(x3, solution);
x4opt = subs(x4, solution);
x5opt = subs(x5, solution);
x6opt = subs(x6, solution);
x7opt = subs(x7, solution);
x8opt = subs(x8, solution);
u1opt = subs(u1, solution);
u2opt = subs(u2, solution);
u3opt = subs(u3, solution);
u4opt = subs(u4, solution);
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Nonlinear CSTR f_k -21.841502289865435000
sum(|constr|) 0.000000000210565355
f(x_k) + sum(|constr|) -21.841502289654869000
f(x_0) 0.000000000000000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 53 ConJacEv 53 Iter 41 MinorIter 342
CPU time: 0.453125 sec. Elapsed time: 0.500000 sec.
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Nonlinear CSTR f_k -21.896802275281718000
sum(|constr|) 0.000000001587400641
f(x_k) + sum(|constr|) -21.896802273694316000
f(x_0) -21.841502289865460000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 96 ConJacEv 96 Iter 91 MinorIter 380
CPU time: 1.500000 sec. Elapsed time: 1.547000 sec.
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Nonlinear CSTR f_k -21.887245712594538000
sum(|constr|) 0.000000000445950436
f(x_k) + sum(|constr|) -21.887245712148587000
f(x_0) -21.896802275281658000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 277 ConJacEv 277 Iter 258 MinorIter 1045
CPU time: 40.765625 sec. Elapsed time: 42.203000 sec.
end
t = subs(collocate(t),solution);
x1 = collocate(x1opt);
x2 = collocate(x2opt);
x3 = collocate(x3opt);
x4 = collocate(x4opt);
x5 = collocate(x5opt);
x6 = collocate(x6opt);
x7 = collocate(x7opt);
x8 = collocate(x8opt);
u1 = collocate(u1opt);
u2 = collocate(u2opt);
u3 = collocate(u3opt);
u4 = collocate(u4opt);
73.5 Plot result
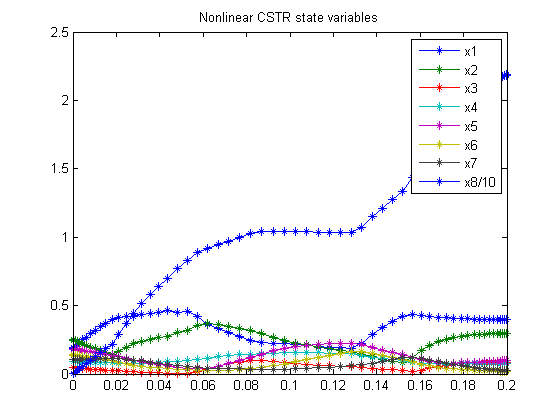
figure(1)
plot(t,x1,'*-',t,x2,'*-',t,x3,'*-',t,x4,'*-' ...
,t,x5,'*-',t,x6,'*-',t,x7,'*-',t,x8/10,'*-');
legend('x1','x2','x3','x4','x5','x6','x7','x8/10');
title('Nonlinear CSTR state variables');
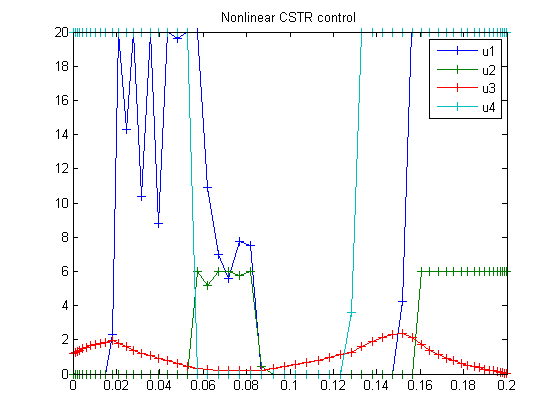
figure(2)
plot(t,u1,'+-',t,u2,'+-',t,u3,'+-',t,u4,'+-');
legend('u1','u2','u3','u4');
title('Nonlinear CSTR control');
« Previous « Start » Next »