« Previous « Start » Next »

81  Parameter Estimation Problem

Example 5: DYNOPT User’s Guide version 4.1.0

M. Cizniar, M. Fikar, M. A. Latifi, MATLAB Dynamic Optimisation Code DYNOPT. User’s Guide, Technical Report, KIRP FCHPT STU Bratislava, Slovak Republic, 2006.

81.1  Problem description

Find p1 and p2 over t in [0; 6 ] to minimize

J =

∑ i=1,2,3,5

( x1(ti) − x1m(ti) )2

subject to:

dx1 dt

= x2

dx2 dt

= 1−2*x2−x1

where

x0 = [p1  p2]

ti = [1  2  3  5]

x1m(ti) = [0.264  0.594  0.801  0.959]

−1.5 <= p1:2 <= 1.5

Reference: [13]

81.2  Problem setup

toms t p1 p2
x1meas = [0.264;0.594;0.801;0.959];
tmeas  = [1;2;3;5];

% Box constraints
cbox = {-1.5 <= p1 <= 1.5
    -1.5 <= p2 <= 1.5};

81.3  Solve the problem, using a successively larger number collocation points

for n=[10 40]

    p = tomPhase('p', t, 0, 6, n);
    setPhase(p);
    tomStates x1 x2

    % Initial guess
    if n == 10
        x0 = {p1 == 0; p2 == 0};
    else
        x0 = {p1 == p1opt; p2 == p2opt
            icollocate({x1 == x1opt; x2 == x2opt})};
    end

    % Boundary constraints
    cbnd = initial({x1 == p1; x2 == p2});

    % ODEs and path constraints
    x1err = sum((atPoints(tmeas,x1) - x1meas).^2);
    ceq = collocate({dot(x1) == x2; dot(x2) == 1-2*x2-x1});

    % Objective
    objective = x1err;

81.4  Solve the problem

    options = struct;
    options.name   = 'Parameter Estimation';
    options.solver = 'snopt';
    solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);

    % Optimal x, p for starting point
    x1opt = subs(x1, solution);
    x2opt = subs(x2, solution);
    p1opt = subs(p1, solution);
    p2opt = subs(p2, solution);

Problem type appears to be: qp
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2011-02-05
=====================================================================================
Problem:  1: Parameter Estimation               f_k       0.000000352979271145
                                       sum(|constr|)      0.000000000000054134
                              f(x_k) + sum(|constr|)      0.000000352979325279
                                              f(x_0)      0.000000000000000000

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 Iter    5 MinorIter   17
CPU time: 0.015625 sec. Elapsed time: 0.016000 sec.

Problem type appears to be: qp
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2011-02-05
=====================================================================================
Problem:  1: Parameter Estimation               f_k       0.000000355693079657
                                       sum(|constr|)      0.000000000000071929
                              f(x_k) + sum(|constr|)      0.000000355693151586
                                              f(x_0)     -1.983813647020728800

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 MinorIter   40
CPU time: 0.015625 sec. Elapsed time: 0.016000 sec.

end

t  = subs(collocate(t),solution);
x1 = collocate(x1opt);

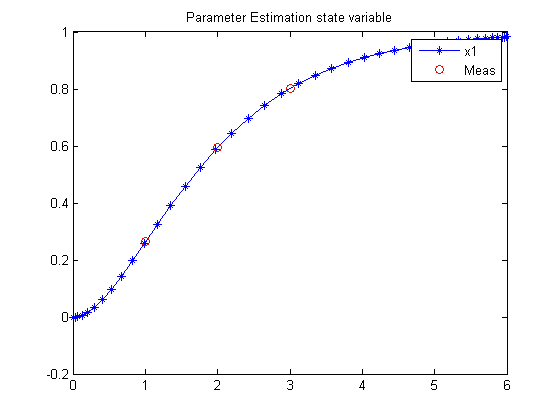
81.5  Plot result

figure(1)
plot(t,x1,'*-',tmeas,x1meas,'ro');
legend('x1','Meas');
title('Parameter Estimation state variable');

« Previous « Start » Next »