« Previous « Start » Next »
38 Free Floating Robot
Users Guide for dyn.Opt, Example 6a, 6b, 6c
A free floating robot
38.1 Problem description
Find u over t in [0; 5 ] to minimize
6c is free end time
6a:
| ∫ | | 0.5*(u12+u22+u32+u42) dt + |
| (x1(tF)−4.0)2+(x3(tF)−4.0)2+x2(tF)2+x4(tF)2+x5(tF)2+x6(tF)2 |
6b:
| ∫ | | 0.5*(u12+u22+u32+u42) dt |
6c:
subject to:
6b - x(5) = [4 0 4 0 0 0]; 6c - x(5) = [4 0 4 0 pi/4 0]; 6c - -5 <= u <= 5
Reference: [16]
38.2 Problem setup
toms t
for i=1:3
if i==3
toms t_f
else
t_f = 5;
end
p1 = tomPhase('p1', t, 0, t_f, 40);
setPhase(p1);
tomStates x1 x2 x3 x4 x5 x6
tomControls u1 u2 u3 u4
% Initial guess
if i==1
x0 = {icollocate({x1 == 0; x2 == 0; x3 == 0
x4 == 0; x5 == 0; x6 == 0})
collocate({u1 == 0; u2 == 0
u3 == 0; u4 == 0})};
elseif i==2
x0 = {icollocate({x1 == x1_init; x2 == x2_init
x3 == x3_init; x4 == x4_init
x5 == x5_init; x6 == x6_init})
collocate({u1 == u1_init; u2 == u2_init
u3 == u3_init; u4 == u4_init})};
else
x0 = {t_f == tf_init
icollocate({x1 == x1_init; x2 == x2_init
x3 == x3_init; x4 == x4_init
x5 == x5_init; x6 == x6_init})
collocate({u1 == u1_init; u2 == u2_init
u3 == u3_init; u4 == u4_init})};
end
% Box constraints
if i<=2
cbox = {icollocate({
-100 <= x1 <= 100; -100 <= x2 <= 100
-100 <= x3 <= 100; -100 <= x4 <= 100
-100 <= x5 <= 100; -100 <= x6 <= 100})
collocate({-1000 <= u1 <= 1000; -1000 <= u2 <= 1000
-1000 <= u3 <= 1000; -1000 <= u4 <= 1000})};
else
cbox = {
icollocate({-100 <= x1 <= 100; -100 <= x2 <= 100
-100 <= x3 <= 100; -100 <= x4 <= 100
-100 <= x5 <= 100; -100 <= x6 <= 100})
collocate({-5 <= u1 <= 5; -5 <= u2 <= 5
-5 <= u3 <= 5; -5 <= u4 <= 5})};
end
% Boundary constraints
cbnd = initial({x1 == 0; x2 == 0; x3 == 0
x4 == 0; x5 == 0; x6 == 0});
if i==2
cbnd6b = {cbnd
final({x1 == 4; x2 == 0
x3 == 4; x4 == 0
x5 == 0; x6 == 0})};
elseif i==3
cbnd6c = {cbnd
final({x1 == 4; x2 == 0
x3 == 4; x4 == 0
x5 == pi/4; x6 == 0
1 <= t_f <= 100})};
end
% ODEs and path constraints
M = 10.0;
D = 5.0;
Le = 5.0;
In = 12.0;
s5 = sin(x5);
c5 = cos(x5);
ceq = collocate({
dot(x1) == x2
dot(x2) == ((u1+u3).*c5-(u2+u4).*s5)/M
dot(x3) == x4
dot(x4) == ((u1+u3).*s5+(u2+u4).*c5)/M
dot(x5) == x6
dot(x6) == ((u1+u3)*D-(u2+u4)*Le)/In});
% Objective
38.3 Solve the problem
options = struct;
if i==1
objective = (final(x1)-4)^2+(final(x3)-4)^2+final(x2)^2+ ...
final(x4)^2+final(x5)^2+final(x6)^2 + ...
integrate(0.5*(u1.^2+u2.^2+u3.^2+u4.^2));
options.name = 'Free Floating Robot 6a';
solution1 = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
tp = subs(collocate(t),solution1);
x1p = subs(collocate(x1),solution1);
x2p = subs(collocate(x2),solution1);
x3p = subs(collocate(x3),solution1);
x4p = subs(collocate(x4),solution1);
x5p = subs(collocate(x5),solution1);
x6p = subs(collocate(x6),solution1);
u1p = subs(collocate(u1),solution1);
u2p = subs(collocate(u2),solution1);
u3p = subs(collocate(u3),solution1);
u4p = subs(collocate(u4),solution1);
tf1 = subs(final(t),solution1);
x1_init = subs(x1,solution1);
x2_init = subs(x2,solution1);
x3_init = subs(x3,solution1);
x4_init = subs(x4,solution1);
x5_init = subs(x5,solution1);
x6_init = subs(x6,solution1);
u1_init = subs(u1,solution1);
u2_init = subs(u2,solution1);
u3_init = subs(u3,solution1);
u4_init = subs(u4,solution1);
elseif i==2
objective = integrate(0.5*(u1.^2+u2.^2+u3.^2+u4.^2));
options.name = 'Free Floating Robot 6b';
solution2 = ezsolve(objective, {cbox, cbnd6b, ceq}, x0, options);
x1_init = subs(x1,solution2);
x2_init = subs(x2,solution2);
x3_init = subs(x3,solution2);
x4_init = subs(x4,solution2);
x5_init = subs(x5,solution2);
x6_init = subs(x6,solution2);
u1_init = subs(u1,solution2);
u2_init = subs(u2,solution2);
u3_init = subs(u3,solution2);
u4_init = subs(u4,solution2);
tf_init = subs(final(t),solution2);
else
objective = t_f;
options.name = 'Free Floating Robot 6c';
solution3 = ezsolve(objective, {cbox, cbnd6c, ceq}, x0, options);
end
Problem type appears to be: qpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Free Floating Robot 6a f_k 13.016949152618082000
sum(|constr|) 0.000000000120833713
f(x_k) + sum(|constr|) 13.016949152738915000
f(x_0) 0.000000000000000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 35 ConJacEv 35 Iter 31 MinorIter 405
CPU time: 1.046875 sec. Elapsed time: 1.156000 sec.
Problem type appears to be: qpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Free Floating Robot 6b f_k 76.800000142684681000
sum(|constr|) 0.000000241108083137
f(x_k) + sum(|constr|) 76.800000383792764000
f(x_0) 6.802639150498469800
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 35 ConJacEv 35 Iter 25 MinorIter 395
CPU time: 0.921875 sec. Elapsed time: 1.031000 sec.
Problem type appears to be: lpcon
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license 999001. Valid to 2011-02-05
=====================================================================================
Problem: --- 1: Free Floating Robot 6c f_k 4.161676034118864100
sum(|constr|) 0.000000000039327186
f(x_k) + sum(|constr|) 4.161676034158190900
f(x_0) 5.000000000000000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 26 ConJacEv 26 Iter 16 MinorIter 570
CPU time: 0.625000 sec. Elapsed time: 0.656000 sec.
end
38.4 Plot result
tf2 = tf_init;
tf3 = subs(t_f,solution3);
disp(sprintf('\nFinal time for 6a = %1.4g',tf1));
disp(sprintf('\nFinal time for 6b = %1.4g',tf2));
disp(sprintf('\nFinal time for 6c = %1.4g',tf3));
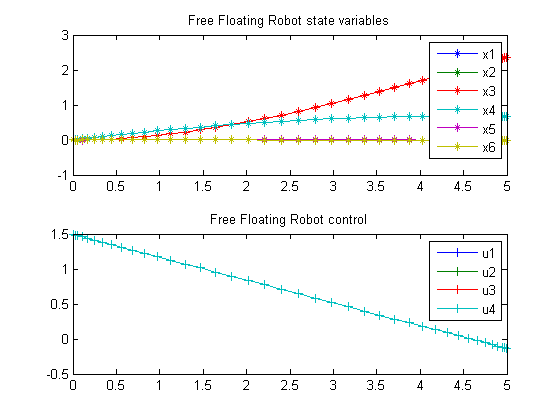
subplot(2,1,1)
plot(tp,x1p,'*-',tp,x2p,'*-',tp,x3p,'*-',tp,x4p,'*-' ...
,tp,x5p,'*-',tp,x6p,'*-');
legend('x1','x2','x3','x4','x5','x6');
title('Free Floating Robot state variables');
subplot(2,1,2)
plot(tp,u1p,'+-',tp,u2p,'+-',tp,u3p,'+-',tp,u4p,'+-');
legend('u1','u2','u3','u4');
title('Free Floating Robot control');
Final time for 6a = 5
Final time for 6b = 5
Final time for 6c = 4.162
« Previous « Start » Next »